代码随想录20 654 最大二叉树

654. 最大二叉树

给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:

1. 创建一个根节点，其值为 nums 中的最大值。
2. 递归地在最大值 左边 的 子数组前缀上 构建左子树。
3. 递归地在最大值 右边 的 子数组后缀上 构建右子树。

返回 nums 构建的 最大二叉树 。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        return helper(nums,0,nums.length);
    }
    private TreeNode helper(int[] nums, int l, int r) {
        if (l == r) return null;
        int maxIdx = findMax(nums, l, r);
        TreeNode root = new TreeNode(nums[maxIdx]);
        root.left = helper(nums, l, maxIdx);
        root.right = helper(nums, maxIdx + 1, r);
        return root;
    }
    private int findMax(int[] nums, int l, int r) {
        int maxIdx = l;
        for (int i = l; i < r; i++) {
            if (nums[i] > nums[maxIdx]) {
                maxIdx = i;
            }
        }
        return maxIdx;
    }
}

617. 合并二叉树

想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

返回合并后的二叉树。

class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        if (root1 == null) return root2;
        if (root2 == null) return root1;

        root2.val += root1.val;
        root2.left = mergeTrees(root1.left, root2.left);
        root2.right = mergeTrees(root1.right, root2.right);
        return root2;
    }
}

700. 二叉搜索树中的搜索

给定二叉搜索树（BST）的根节点 root 和一个整数值 val。

你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 null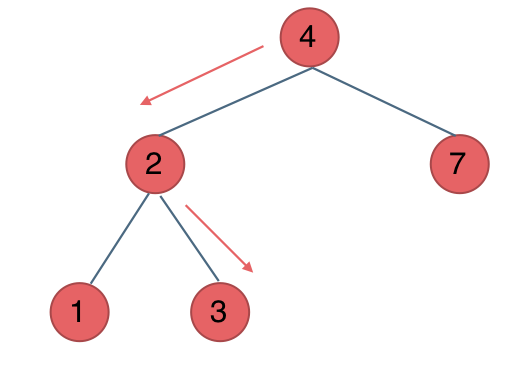 

class Solution {
    public TreeNode searchBST(TreeNode root, int val) {
        if (root == null || root.val == val) {
            return root;
        }
        if (val < root.val) {
            return searchBST(root.left, val);
        } else {
            return searchBST(root.right, val);
        }
    }
}

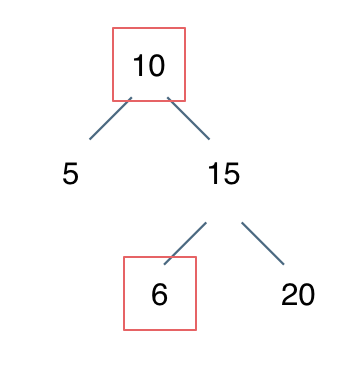
98. 验证二叉搜索树

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

• 节点的左子树只包含 小于 当前节点的数。
• 节点的右子树只包含 大于 当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。
  
  

  class Solution {
      TreeNode max;
      public boolean isValidBST(TreeNode root) {
          if (root == null) return true;
          boolean left = isValidBST(root.left);
          if (!left) return false;
          if (max != null && root.val <= max.val) {
              return false;
          }
          max = root;
          boolean right = isValidBST(root.right);
          return right;
      }
  }