主要思想
树链剖分(简称树剖)的思想在于将一棵树剖分为若干条链,从而转化为一个线性序列并使用数据结构维护来解决问题。
以下主要讲两种:一种是重链剖分,一种是长链剖分。
重链剖分
原理
重链剖分可以将树上的任意一条路径划分成不超过 \(O(\log n)\) 条连续的链,同时通过一个特殊的 dfs 保证同一条链上节点的 \(dfn\) 连续从而可以十分方便地使用线段树等数据结构进行维护树上一条路径的信息。
同时,每条链上节点的深度都是互不相同的,所以树剖也可以用于求解 LCA。
这里列出一些使用场景:
-
维护树上路径上的信息。
-
维护以一个节点为根的一棵子树上的信息。
实现
首先,给出一些定义:
重子节点:其子节点中拥有最大子树(以该儿子节点为根)的儿子节点。如果有多个随便取一个,如果是叶子节点则无重子节点。
轻子节点:不是重子节点的节点。
重边:该节点到它的重子节点的边。
轻边:该节点到它的轻子节点的边。
重链:若干条首尾衔接的重边。
如果我们把单独的一个节点也当作一条重链,那么整棵树就被剖分为若干条重链。
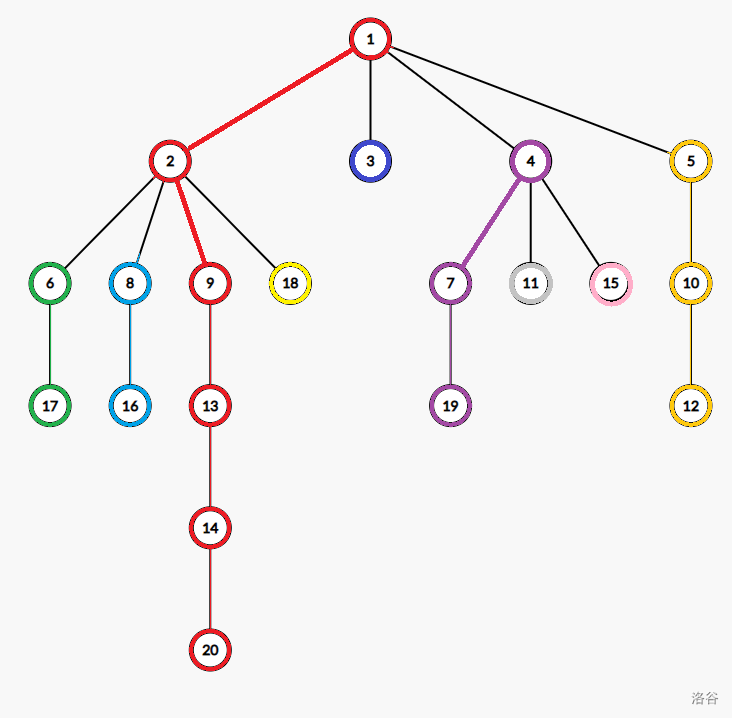
图中每一个颜色都代表着一条重链。
实现树剖,我们需要两次 dfs。
第一次 dfs 记录每个结点的父节点、深度、子树大小以及重子节点。
第二次 dfs 记录特殊 dfs 序下的 \(dfn\)(特殊 dfs 序为优先遍历重儿子。因为这样方便记录重链并且保证重链的 \(dfn\) 连续)、每条重链的链顶以及每个 \(dfn\) 对应的节点编号(可是我不知道有啥用)。
习题1 【模板】重链剖分/树链剖分
思路
重链剖分,然后线段树维护即可。
代码
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+10;
int n,m,root,mod;
int val[maxn],cnt,size[maxn],son[maxn],top[maxn],dep[maxn],f[maxn],valt[200005],id[maxn];
struct node{
int val,tag,l,r;
}a[maxn*4];
vector<int> G[maxn];
void down(int v){
a[v*2].tag=(a[v*2].tag+a[v].tag)%mod;
a[v*2+1].tag=(a[v*2+1].tag+a[v].tag)%mod;
a[v*2].val=(a[v*2].val+a[v].tag*(a[v*2].r-a[v*2].l+1))%mod;
a[v*2+1].val=(a[v*2+1].val+a[v].tag*(a[v*2+1].r-a[v*2+1].l+1))%mod;
a[v].tag=0;
}
void add(int u,int l,int r,int v){
if(l<=a[u].l&&r>=a[u].r){
a[u].val=(a[u].val+v*(a[u].r-a[u].l+1))%mod;
a[u].tag=(a[u].tag+v)%mod;
return;
}
if(a[u].tag){
down(u);
}
int mid=(a[u].l+a[u].r)/2;
if(l<=mid){
add(u*2,l,r,v);
}
if(r>mid){
add(u*2+1,l,r,v);
}
a[u].val=(a[u*2].val+a[u*2+1].val)%mod;
}
int find(int u,int l,int r){
int val1=0;
if(l<=a[u].l && r>=a[u].r){
a[u].val=a[u].val%mod;
return a[u].val;
}
if(a[u].tag){
down(u);
}
int mid=(a[u].l+a[u].r)/2;
if(l<=mid){
val1=(find(u*2,l,r)+val1)%mod;
}
if(r>mid){
val1=(find(u*2+1,l,r)+val1)%mod;
}
return val1;
}
void dfs1(int u,int fa,int depth){
dep[u]=depth;
f[u]=fa;
size[u]=1;
for(int i=0;i<G[u].size();i++){
int v=G[u][i];
if(v!=fa){
dfs1(v,u,depth+1);
size[u]+=size[v];
if(size[v]>size[son[u]]){
son[u]=v;
}
}
}
}
void dfs2(int u,int nowtop){
id[u]=++cnt;
valt[cnt]=val[u];
top[u]=nowtop;
if(son[u]){
dfs2(son[u],nowtop);
for(int i=0;i<G[u].size();i++){
int v=G[u][i];
if(v!=f[u]&&v!=son[u]){
dfs2(v,v);
}
}
}
}
void build(int u,int l,int r){
a[u].l=l;
a[u].r=r;
a[u].tag=0;
if(l==r){
a[u].val=valt[l];
a[u].val=a[u].val%mod;
return;
}
int mid=(l+r)/2;
build(u*2,l,mid);
build(u*2+1,mid+1,r);
a[u].val=(a[u*2].val+a[u*2+1].val)%mod;
}
void updateintree(int x,int y,int val1){
val1%=mod;
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]])
swap(x,y);
add(1,id[top[x]],id[x],val1);
x=f[top[x]];
}
if(dep[x]>dep[y])
swap(x,y);
add(1,id[x],id[y],val1);
}
int queryintree(int x,int y){
int val2=0;
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]])
swap(x,y);
val2=find(1,id[top[x]],id[x])+val2;
val2%=mod;
x=f[top[x]];
}
if(dep[x]>dep[y])
swap(x,y);
val2=find(1,id[x],id[y])+val2;
val2%=mod;
return val2;
}
void update(int root3,int val21){
add(1,id[root3],id[root3]+size[root3]-1,val21);
}
int query(int root4){
int val3=0;
val3=find(1,id[root4],id[root4]+size[root4]-1)%mod;
return val3;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n>>m>>root>>mod;
for(int i=1;i<=n;i++){
cin>>val[i];
val[i]%=mod;
}
for(int i=1;i<n;i++){
int u,v;
cin>>u>>v;
G[u].push_back(v);
G[v].push_back(u);
}
dfs1(root,0,1);
dfs2(root,root);
build(1,1,n);
for(int i=1;i<=m;i++){
int op,x,y,z;
cin>>op;
if(op==1){
cin>>x>>y>>z;
updateintree(x,y,z);
}
if(op==2){
cin>>x>>y;
cout<<queryintree(x,y)<<endl;
}
if(op==3){
cin>>x>>y;
update(x,y);
}
if(op==4){
cin>>x;
cout<<query(x)<<endl;
}
}
return 0;
}