由于我很菜,连这种基本的问题都不能做到百分百会证明,会运用,所以我就来写一下来加深影响。
Umnik 子云:Stop learning useless algorithm!
选择最多不相交区间
我们想怎么解决这个问题呢?首先会把它在数轴上画出来对吧,比如 \([4, 8], [1, 4], [2, 5], [3, 6]\),我们可以画成这个样子 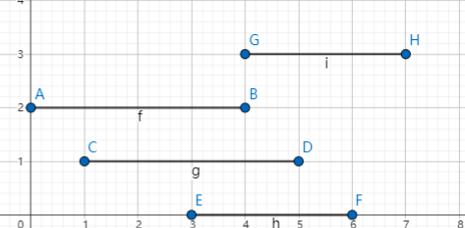
我们很容易想到这样一个贪心策略:每次都选一个 \(r\) 尽量小的区间,这样能对后面的区间影响尽量小。
好了,先按照 \(r\) 从小到大排序,那么比如我们处理一个 \(r_i\),我们是不去管 \(0\sim i - 1\) 的线段的(贡献已经计算过)。对于上面这种情况,我们会自然而然的选择 \(r\) 最小的 AB,因为它 \(r\) 最小,对剩下的线段影响最小。
对于 \(r\) 相等的情况,那么很显然我们会选择 \(l\) 更大的线段。
选了 AB 后,我们怎么做?很显然,我们会排除 CD,EF,GH(因为它们和 AB 香蕉)。
我们其实得到了我们的算法:
- 以 \(r\) 为第一关键字升序排序,\(l\) 为第二关键字降序排序。
- 从 \(1\sim n\) 扫描,选择 \(i\),排除后面与 \(i\) 相交的区间。
值得一提的是,虽然理论上我们要按照 \(l\) 为第二关键字降序排序,但是实践中我们可以把这一行上去。为什么呢?因为我们推导过程中,是不去管 \(0\sim i - 1\) 的线段的。也就是说它左端点伸出到哪里是不重要的,重要的是:它不和前面选得区间相交。
额但是最好还是加这一句吧,毕竟觉得好像更正确一点(雾)
用最少的点覆盖所有区间
我们很容易想到这样一个贪心策略:每次选择一个区间的最后一点。这样才能影响最大化,
我们会选择 AB 的最后一个端点 4,这样就刚好能覆盖所有区间了。我们会得到一个类似的贪心策略:
- 以 \(r\) 为第一关键字升序排序,\(l\) 为第二关键字降序排序。
以 \(r\) 为第一关键字升序排序,和上面目的一样,使我们后面的决策不会影响到前面的。
\(l\) 的排序目的也一样,是为了让我们能先处理小区间。 - \(1\sim n\) 扫描,选择 \(r_i\) 这个点覆盖,把所有包含 \(r_i\) 的区间排除掉,继续做。
很显然,我们会选择 \(r_i\) 这个点,这显然不会对后面和之前的决策产生任何影响,而且这显然是最优的。
区间覆盖问题
给定 \(n\) 个区间,用最少的区间覆盖给定的区间 \([s, t]\)。
我们容易想到这样一个贪心策略:每次选择一个覆盖尽量多的一个区间。
比如我们要覆盖 \([5, 10]\),然后我们有两个区间 \([1, 5]\) 与 \([5, 6]\)。这里我们就会选择 \([5, 6]\),因为它覆盖了 \([5, 10]\) 中两个单位,而 \([1, 5]\) 只有一个单位。
具体一点来说,我们可以把所有与 \([s, t]\) 不相交的区间砍掉,对于 \(l_i < s, s \le r_i \le t\) 的区间,我们就把 \(l_i = s\),这是因为 \([l_i, s - 1]\) 这部分没有任何影响。下面就好办了,根据我们的贪心策略,首先我们找到一个左端点为 \(s\) 的,右端点尽量大的区间,我们选它,这时候没有覆盖的区间变成了 \([r_i + 1, t]\) 了。然后就一直这样做下去就可以了。
这是一个理论化的算法,当然咯时间里面不可能说真的把多出的那段给“砍掉”。我们很容易想到这样一个方法:
- 所有点按照 \(l\) 升序排序。
- 从 \(1\sim n\) 扫描 \(i\)。
- 如果 \(l_i > s\),直接无解。
- 如果 \(l_i \le s\),那么就往后扫描,最终可以得到满足 \(l_j \le s\) 的最大的 \(r_j\),我们就选择这个区间 \(j\),未覆盖区间变成了 \([r_j + 1, t]\)。注意如果有一些区间我们在这里没选中,那么后面更不会选中,所以我们可以让 \(i = j + 1\)。
总结一下我们是如何解决这三个问题的:
首先可以先想一个大致的贪心策略,然后手玩一个小数据,然后就差不多得到了一个简单的算法的雏形,随便缝缝补补即可。
标签:覆盖,幼儿园,区间,排序,我们,sim,贪心 From: https://www.cnblogs.com/thirty-two/p/17231244.html