前情提要

前言
相信大家都听说过 \(\text{Splay}\) 的常数大。
相信大家都听说过 \(\text{FHQ-Treap}\) 的常数小。
但是现在我要说的是:你说得对,但是你说得不对。
所谓常数
一般测试代码的常数,我们会直接生成一组数据直接跑,根据运行时间来估测。这里就是一些测试记录。
可以发现,在运行时间这一块,结果和你所想象和认为的一样:\(\text{Treap}\) 比 \(\text{Splay}\) 跑得快。这点我不否认,毋庸置疑的,测试结果摆在这里。
但是,你可以看见,我们记录了额外的东西:pushup 的调用次数。
把这个 pushup 调用次数放上来,结果可就大不相同了。\(\text{Treap}\) 的 pushup 次数大于是 \(\text{Splay}\) 的两倍,从这个角度上来看,\(\text{Treap}\) 的常数是远远劣于 \(\text{Splay}\) 的!
在我们实际使用平衡树的时候,我们的 pushup 绝大多数时候不会是简单的更新子树大小(当然我们也会有 lazytag 和 pushdown 等操作,但一般而言,pushdown 和 pushup 的调用次数是相当的)。\(\text{Splay}\) 的常数主要来源是它的维护方式:\(\text{Splay}\) 节点需要维护左右儿子和父亲三个指针,在旋转的时候有一系列复杂的操作,会因为内存访问等原因使得速度较慢。
在这个测试中,因为维护的信息十分简单,运行时间的瓶颈就在平衡树形态维护上面了。但是如果维护的信息复杂起来,合并的复杂度高起来(比如,你在维护最大子段和,又或者你需要打区间翻转标记),瓶颈就会转移到 pushup 的调用次数上。这时候,\(\text{Splay}\) 就会显现出优势。
所以我们可以得到结论:如果你的平衡树仅仅是维护有序集合,那么用 \(\text{Treap}\) 是比 \(\text{Splay}\) 优秀的。但若是要维护区间信息,进行区间操作,还是用 \(\text{Splay}\) 会更好一些。
找不到除了 yyds 之外的形容词来描述 \(\text{RB Tree}\)。
你应该发现那里面有个叫做 \(\text{Leafy-Splay}\) 的怪物,这个后文会提到。
常数优化
接下来会提一些 Splay 的常数优化。
储存结构
首先是储存儿子指针,大部分人会写成 int ch[2],fa;,原因是这样在旋转的时候可以减少一些讨论。
但是我建议大家直接写成 int lc,rc,fa;,原因有两个:反复取下标运算其实是一件浪费的事情,速度会慢,具体会慢多少没有测量过,但是的确是慢的;在进行树上的操作时候,经常需要访问左右儿子指针,这时候 ch[0],ch[1] 就会显得冗长而不直观,使用 lc,rc 会好很多。
下面是一段使用 lc,rc 储存的 \(\text{ROTATE}\) 操作代码(使用了指针):
inline void rotate(pNode i)
{
pNode f=i->fa,gf=f->fa;
pushdown(f),pushdown(i);
if(islc(i)) f->lc=i->rc,i->rc=f,f->lc&&(f->lc->fa=f);
else f->rc=i->lc,i->lc=f,f->rc&&(f->rc->fa=f);
if(gf) (islc(f)?gf->lc:gf->rc)=i;
f->fa=i,i->fa=gf;
pushup(f),pushup(i);
}
pNode 是指向节点的指针,islc(i) 判断节点 \(i\) 是不是左儿子。
于是你就会发现,代码并没有复杂多少!如果在使用数组而非指针的情况下,代码可以省略空指针判断部分,甚至能够更短。
你需要 pushup 吗?
废话,当然需要。
但是你先别急,我们把代码改成这样:
inline void rotate(pNode i)
{
pNode f=i->fa,gf=f->fa;
pushdown(f),pushdown(i);
if(islc(i)) f->lc=i->rc,i->rc=f,f->lc&&(f->lc->fa=f);
else f->rc=i->lc,i->lc=f,f->rc&&(f->rc->fa=f);
if(gf) (islc(f)?gf->lc:gf->rc)=i;
f->fa=i,i->fa=gf,pushup(f);
}
inline void splay(pNode x,pNode goal=nullptr)
{
for(pNode f;(f=x->fa)!=goal;rotate(x))
if(f->fa!=goal)
rotate(islc(f)==islc(x)?f:x);
pushup(x),goal||(rt=x);
}
\(\text{ROTATE}\) 操作内的 pushup 次数降到了一次,但是仍然保证正确性。
仔细分析,在进行 \(\operatorname{ROTATE}(x)\) 的时候,会把 \(x\) 的父亲节点“扔出”\(x\) 到根的链,而 \(x\) 则继续往上“攀爬”。因为 \(x\) 一直在往上爬,所以我们可以等到最后更新 \(x\) 的信息,\(\text{ROTATE}\) 的时候就只需要 pushup 原父亲节点了。
具体的分析需要分单旋双旋讨论,这里不赘述,给两张图:
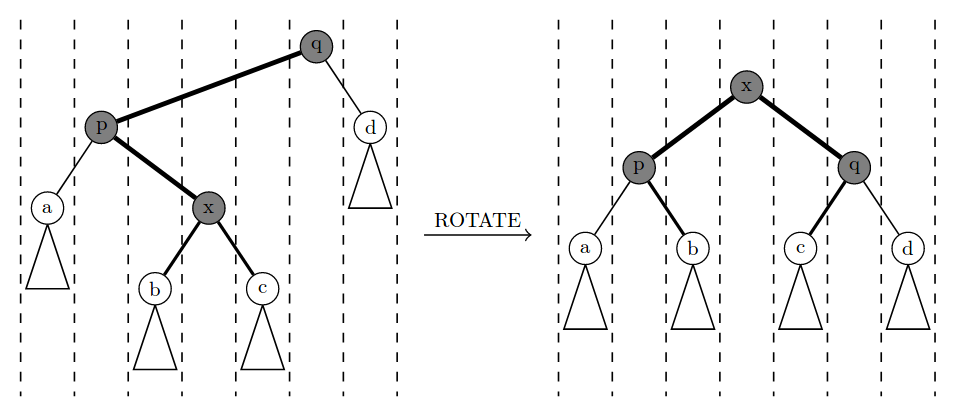
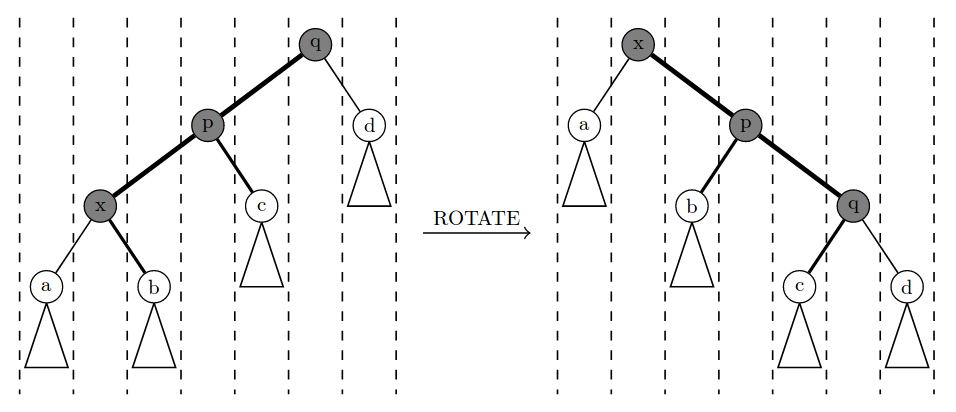
你需要 pushdown 吗?
不难发现,需要 pushdown 的节点只是 \(x\) 到根的路径节点。
可以想到,提前 pushup 会省下不少事情。
inline void rotate(pNode i)
{
pNode f=i->fa,gf=f->fa;
if(islc(i)) f->lc=i->rc,i->rc=f,f->lc&&(f->lc->fa=f);
else f->rc=i->lc,i->lc=f,f->rc&&(f->rc->fa=f);
if(gf) (islc(f)?gf->lc:gf->rc)=i;
f->fa=i,i->fa=gf,pushup(f);
}
inline void pushall(pNode x)
{
if(!x) return;
pushall(x->fa);
pushdown(x);
}
inline void splay(pNode x,pNode goal=nullptr)
{
pushall(x);
for(pNode f;(f=x->fa)!=goal;rotate(x))
if(f->fa!=goal)
rotate(islc(f)==islc(x)?f:x);
pushup(x),goal||(rt=x);
}
这也是我们在写 LCT 时常干的事情。
当然,你可以用数组模拟栈来代替递归,会快一点点。
你需要 pushall 吗?
这么问就有些离谱了,但你先别急。
\(\text{SPLAY}\) 操作用处是均摊掉在从根开始搜到 \(x\) 所用的时间。
大部分时候,你在搜索的过程中就会 pushdown 了。
于是 pushall 也被省略了!现在你的 Splay 中没有任何一点点没有的 pushdown/pushup。
\(\text{Leafy-Splay}\) 简介。
这一部分才是重点,但是今天没时间了,明天再写。
标签:横空出世,lc,text,Splay,fa,pushup,rc,Leafy From: https://www.cnblogs.com/ExplodingKonjac/p/17220177.html