第六章 贪心一
区间问题
区间选点
给定 N 个闭区间 [ai,bi],请你在数轴上选择尽量少的点,使得每个区间内至少包含一个选出的点。
输出选择的点的最小数量。
位于区间端点上的点也算作区间内。
输入格式
第一行包含整数 N,表示区间数。
接下来 N 行,每行包含两个整数 ai,bi,表示一个区间的两个端点。
输出格式
输出一个整数,表示所需的点的最小数量。
数据范围
1≤N≤10^5,
−109≤ai≤bi≤109
输入样例:
3
-1 1
2 4
3 5
输出样例:
2
分析
- 将每个区间按照右端点从小到大排序
- 从前往后依次枚举每个区间
- 若当前区间中已经包含点,则跳过
- 否则,选择当前区间的右端点
证明
因为区间是按照右端点从小到大排序的,所以在某个区间内选点的时候,只有选择右端点,才能尽可能的使得这个点覆盖掉后续更多的区间。
设按照上面的策略,选出的点数为cnt,问题的答案为ans。那么我们就是要证明cnt = ans。
在数学上有一个思路,若要证A = B,则可以先证A >= B,再证 A <= B,以此得出 A = B。即,用不等式来推导出等式。
首先,按照上面的策略选点完毕后,能保证每个区间都至少有一个点。因为我们会依次枚举每个区间,若当前区间包含点,就跳过,若不包含,就选一个点。所以最终每个区间都至少有一个点。也就是说,通过这个策略得到的,一定是一个合法的选点方案(每个区间内都至少包含一个点即为合法)。而问题的答案,就是全部合法方案中的最小值。所以我们能得出:ans <= cnt
接着,我们换一种角度,按照上面的策略,什么时候会增加一个点呢?那就是从前往后枚举每个区间时,遇到了当前区间没有点这个分支条件时,才会实际上增加一个点。那我们通过上面的策略最终选出了cnt个点,也就是有cnt个区间走到了当前区间没有点这个分支上。而由于区间是按照右端点从小到大排序的,那么我们能从全部的区间中,抽取出cnt个区间,这cnt个区间从左到右依次排列,且两两不相交。
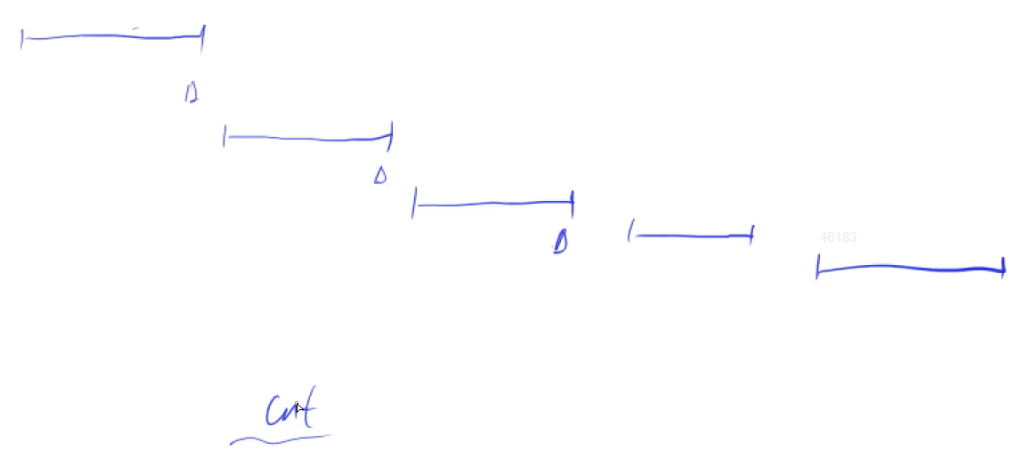
由于合法的方案,需要保证每个区间内都至少有一个点,所以,所有的合法方案,都必须要覆盖掉这cnt个两两不相交的区间,而覆盖掉这cnt个区间,至少需要cnt个点。所以,所有的合法方案的点数,都一定要大于等于cnt。而问题的解也是合法方案中的一种,所以它也要满足大于等于cnt。于是就有了:ans >= cnt
根据ans <= cnt 和 ans >= cnt,我们就能得出 ans = cnt。
Code
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 100010;
struct Range {
int l, r;
bool operator< (const Range &w) const {
return r < w.r;
}
} range[N];
int n;
int main () {
cin >> n;
for (int i = 0; i < n; i++) {
int a, b;
cin >> a >> b;
range[i] = {a, b};
}
sort(range, range + n);
int cnt = 0, ed = -2e9;
for (int i = 0; i < n; i++) {
if (range[i].l > ed) {
cnt++;
ed = range[i].r;
}
}
cout << cnt << endl;
return 0;
}
最大不相交区间数量
给定 N个闭区间 [ai,bi],请你在数轴上选择若干区间,使得选中的区间之间互不相交(包括端点)。
输出可选取区间的最大数量。
输入格式
第一行包含整数 N,表示区间数。
接下来 N 行,每行包含两个整数 ai,bi,表示一个区间的两个端点。
输出格式
输出一个整数,表示可选取区间的最大数量。
数据范围
1≤N≤10^5
−109≤ai≤bi≤109
输入样例:
3
-1 1
2 4
3 5
输出样例:
2
分析
这道题和上道题一模一样
证明
按照上面的策略,我们能选出cnt个区间,这些区间之间两两不相交。

那么这是一种合法的方案(选出的所有区间之间不能相交,即为合法)。而问题的答案ans,是所有合法方案中,区间数量最大的那种方案。所以ans >= cnt。
对于ans <= cnt的证明,可以考虑使用反证法。先假设ans > cnt,看有没有什么矛盾。
假设ans > cnt,则说明可以选择出ans个互不相交的区间,那么要覆盖掉全部的区间,则至少需要ans个点。而根据我们上面的策略,能够得知,只需要cnt个点,就能够把全部的区间覆盖完毕。
也就是说,如果存在ans > cnt,则至少需要ans(大于cnt)个点,才能覆盖掉全部的区间,这与只需要cnt个点就能覆盖掉全部的区间矛盾了。所以ans > cnt不成立,即ans <= cnt成立。
Code
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 100010;
struct Range {
int l, r;
bool operator< (const Range &w) const {
return r < w.r;
}
} range[N];
int n;
int main () {
cin >> n;
for (int i = 0; i < n; i++) {
int a, b;
cin >> a >> b;
range[i] = {a, b};
}
sort(range, range + n);
int cnt = 0, ed = -2e9;
for (int i = 0; i < n; i++) {
if (range[i].l > ed) {
cnt++;
ed = range[i].r;
}
}
cout << cnt << endl;
return 0;
}
区间分组
给定 N 个闭区间 [ai,bi],请你将这些区间分成若干组,使得每组内部的区间两两之间(包括端点)没有交集,并使得组数尽可能小。
输出最小组数。
输入格式
第一行包含整数 N,表示区间数。
接下来 N 行,每行包含两个整数 ai,bi,表示一个区间的两个端点。
输出格式
输出一个整数,表示最小组数。
数据范围
1≤N≤10^5
−109≤ai≤bi≤109
输入样例:
3
-1 1
2 4
3 5
输出样例:
2
分析
- 将所有区间按照左端点从小到大排序
- 从前往后处理每个区间
- 判断能否将当前区间放到某个现有的组当中(判断现有组中的最后一个区间的右端点,是否小于当前区间的左端点)
- 如果不存在这样的组,就意味着当前区间,与所有的组都有交集,就必须要开一个新的组,把这个区间放进去,如果存在这样的组,就将当前区间放到这个组中,并更新这个组
证明
ans表示最终答案,cnt表示按照上述算法得到的分组数量,仍然从两方面来证明ans <= cnt ,ans >= cnt 。
首先,按照上面的算法步骤,得到的方案一定是一个合法方案,因为任意两个组之间都不会有交集,然后ans是所有合法方案中的最小值,故有ans <= cnt。
然后,观察一下最后一个新开的组的情况,什么情况需要新开一个组呢?当某个区间和现有的所有分组都有交集时,则需要新开一个组。当新开第cnt个组时,则当前这个区间和其余的cnt-1个组都有交集,而区间的左端点是从小到大排列的。设当前这个区间的左端点为L,则全部的cnt个分组,都有一个公共的点L。也就是说,至少有cnt个区间,在L这个点上是相交的。故要把这些区间分开来,则至少要分cnt个组。即,ans >= cnt。由此得ans = cnt,得证。
Code
#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
using namespace std;
const int N = 1e5 + 10;
int n;
struct Range {
int l, r;
bool operator < (const Range &w) {
return l < w.l;
}
} range[N];
int main() {
scanf("%d", &n);
for(int i = 0; i < n; i++) {
int l, r;
scanf("%d%d", &l, &r);
range[i] = {l, r};
}
sort(range, range + n);
// 用小根堆来维护每个分组的最右端点
priority_queue<int, vector<int>, greater<int>> heap;
for(int i = 0; i < n; i++) {
auto r = range[i];
// 若堆为空, 或堆顶(所有组的右端点的最小值)大于等于当前区间的左端点, 则需要新开一个组
if(heap.empty() || heap.top() >= r.l) heap.push(r.r);
else {
// 否则, 可以插入到堆顶这个组, 则更新堆顶这个组的右端点
heap.pop();
heap.push(r.r);
}
}
printf("%d\n", heap.size());
return 0;
}
区间覆盖
给定 N个闭区间 [ai,bi]以及一个线段区间 [s,t],请你选择尽量少的区间,将指定线段区间完全覆盖。
输出最少区间数,如果无法完全覆盖则输出 −1−1。
输入格式
第一行包含两个整数 s 和 t,表示给定线段区间的两个端点。
第二行包含整数 N,表示给定区间数。
接下来 N 行,每行包含两个整数 ai,bi,表示一个区间的两个端点。
输出格式
输出一个整数,表示所需最少区间数。
如果无解,则输出 −1。
数据范围
1≤N≤10^5
−109≤ai≤bi≤109
−109≤s≤t≤109
输入样例:
1 5
3
-1 3
2 4
3 5
输出样例:
2
分析
设线段的左端点为start,右端点为end
- 将所有区间按照左端点从小到大排序
- 从前往后依次枚举每个区间,在所有能覆盖
start的区间中,选择一个右端点最大的区间,随后,将start更新为选中区间的右端点 - 当
start >= end,结束

首先,(在有解的前提下)上面的策略可以找出一个可行的合法方案,将这个方案需要用到的区间数量记为cnt,而ans表示的是所有合法方案中的最少区间数量,所以有ans <= cnt。
接着,假设ans < cnt,则在ans选择区间时,一定从某个区间开始,和cnt的选择不一样。而cnt每次是选择能覆盖当前start,且右端点最大的区间,则可以将ans该次的选择,用cnt的选择替换掉,且不会增加所选区间的个数。依次往后推,可以得出ans一定是等于cnt的。
Code
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 100010;
struct Range {
int l, r;
bool operator< (const Range &w) const {
return l < w.l;
}
} range[N];
int n, st, ed;
int main() {
cin >> st >> ed;
cin >> n;
for (int i = 0; i < n; i++) {
int l, r;
cin >> l >> r;
range[i] = {l, r};
}
sort(range, range + n);
bool success = false;
int res = 0;
for (int i = 0; i < n; i++) {
int j = i, r = -2e9;
while (j < n && range[j].l <= st) r = max(r, range[j++].r);
if (r < st) {
res = -1;
break;
}
res++;
if (r >= ed) {
success = true;
break;
}
st = r;
i = j - 1;
}
if(!success) res = -1;
cout << res << endl;
return 0;
}
合并果子
在一个果园里,达达已经将所有的果子打了下来,而且按果子的不同种类分成了不同的堆。
达达决定把所有的果子合成一堆。
每一次合并,达达可以把两堆果子合并到一起,消耗的体力等于两堆果子的重量之和。
可以看出,所有的果子经过 n−1 次合并之后,就只剩下一堆了。
达达在合并果子时总共消耗的体力等于每次合并所耗体力之和。
因为还要花大力气把这些果子搬回家,所以达达在合并果子时要尽可能地节省体力。
假定每个果子重量都为 11,并且已知果子的种类数和每种果子的数目,你的任务是设计出合并的次序方案,使达达耗费的体力最少,并输出这个最小的体力耗费值。
例如有 33 种果子,数目依次为 1,2,9。
可以先将 1、2堆合并,新堆数目为 3,耗费体力为 3。
接着,将新堆与原先的第三堆合并,又得到新的堆,数目为 12,耗费体力为 12。
所以达达总共耗费体力=3+12=15。
可以证明 15 为最小的体力耗费值。
输入格式
输入包括两行,第一行是一个整数 n,表示果子的种类数。
第二行包含 n 个整数,用空格分隔,第 i 个整数 ai 是第 i 种果子的数目。
输出格式
输出包括一行,这一行只包含一个整数,也就是最小的体力耗费值。
输入数据保证这个值小于 231。
数据范围
1≤n≤10000
1≤ai≤20000
输入样例:
3
1 2 9
输出样例:
15
分析
果子的合并过程,可以用一棵树来表示
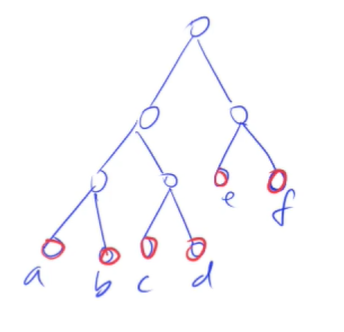
所有的叶子节点,是每一堆果子的重量,而每个非叶子节点,就表示了一次合并操作消耗的体力。则消耗的总体力,就是全部非叶子节点的总和。比如,对于a这个节点,我们可以看到,其需要参与3次合并,a会被累加3次,被累加的次数也是这个节点到根节点的路径长度。
所以,要使得消耗的总的体力最小,我们需要使权重大的节点(消耗体力大的节点),到根节点的路径尽可能的短(使得这个节点被计算的次数尽可能少)。
这就跟哈夫曼编码一个道理
Code
#include<iostream>
#include<queue>
#include<algorithm>
using namespace std;
int main() {
int n, res = 0;
cin >> n;
priority_queue<int, vector<int>, greater<int>> heap;
for (int i = 0; i < n; i++) {
int x;
cin >> x;
heap.push(x);
}
while (heap.size() > 1) {
int a = heap.top();
heap.pop();
int b = heap.top();
heap.pop();
res += a + b;
heap.push(a + b);
}
cout << res << endl;
return 0;
}