问题
Alice 有一棵 n 个节点的树,节点编号为 0 到 n - 1 。树用一个长度为 n - 1 的二维整数数组 edges 表示,其中 edges[i] = [ai, bi] ,表示树中节点 ai 和 bi 之间有一条边。
Alice 想要 Bob 找到这棵树的根。她允许 Bob 对这棵树进行若干次 猜测 。每一次猜测,Bob 做如下事情:
- 选择两个 不相等 的整数
u和v,且树中必须存在边[u, v]。 - Bob 猜测树中
u是v的 父节点 。
Bob 的猜测用二维整数数组 guesses 表示,其中 guesses[j] = [uj, vj] 表示 Bob 猜 uj 是 vj 的父节点。
Alice 非常懒,她不想逐个回答 Bob 的猜测,只告诉 Bob 这些猜测里面 至少 有 k 个猜测的结果为 true 。
给你二维整数数组 edges ,Bob 的所有猜测和整数 k ,请你返回可能成为树根的 节点数目 。如果没有这样的树,则返回 0。
示例
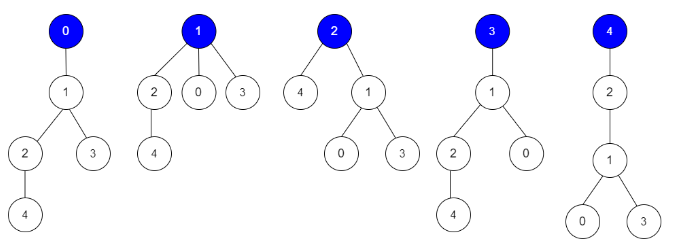
输入:edges = [[0,1],[1,2],[1,3],[4,2]], guesses = [[1,3],[0,1],[1,0],[2,4]], k = 3
输出:3
解释:
根为节点 0 ,正确的猜测为 [1,3], [0,1], [2,4]
根为节点 1 ,正确的猜测为 [1,3], [1,0], [2,4]
根为节点 2 ,正确的猜测为 [1,3], [1,0], [2,4]
根为节点 3 ,正确的猜测为 [1,0], [2,4]
根为节点 4 ,正确的猜测为 [1,3], [1,0]
节点 0 ,1 或 2 为根时,可以得到 3 个正确的猜测。
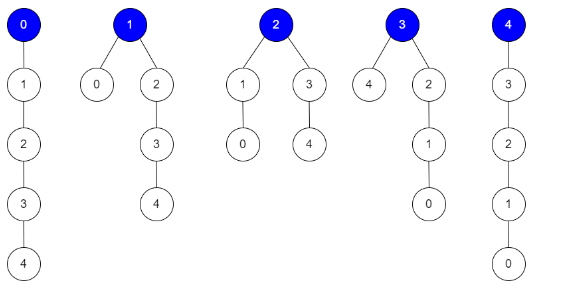
输入:edges = [[0,1],[1,2],[2,3],[3,4]], guesses = [[1,0],[3,4],[2,1],[3,2]], k = 1
输出:5
解释:
根为节点 0 ,正确的猜测为 [3,4]
根为节点 1 ,正确的猜测为 [1,0], [3,4]
根为节点 2 ,正确的猜测为 [1,0], [2,1], [3,4]
根为节点 3 ,正确的猜测为 [1,0], [2,1], [3,2], [3,4]
根为节点 4 ,正确的猜测为 [1,0], [2,1], [3,2]
任何节点为根,都至少有 1 个正确的猜测。
分析
这道题考察的是【换根DP】
先考虑暴力做法,就是枚举每个节点作为根节点,然后进行dfs,统计答案,而使用换根dp则是通过一下几个步骤来进行求解的
- 随便选一个点作为根节点,通过一次dfs收集我们需要的信息
- 考虑如果更换树根,答案能否通过上一次收集的信息转化而来,不再枚举剩余的节点作为根节点再dfs整颗树
- 再进行一次dfs,dfs的过程就是换根的过程,通过已经收集的信息推出答案
- 一共只需要两次dfs
对于本题,我们发现更换根节点只影响新的树根和他原来的父节点的父子关系,比如:
在示例一中,将根由0换成1,那么[0, 1]就由正确的变为错误的,而[1, 0]就由错误的变成了正确的了,即cnt1 = cnt0 - [0, 1] in guesses + [1, 0] in guesses,因此:
- 把以 0 为根节点进行一次dfs,计算出猜对的次数
cnt0 - 再跑一遍dfs,进行换根,根据已知的信息推出不同的根下的猜对的次数
Code
class Solution {
static const int N = 100010, M = 2 * N;
int h[N], e[M], ne[M], idx = 0;
int cnt0 = 0, res = 0, k;
set<long > s;
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void dfs1(int u, int p) {
for (int i = h[u]; i != -1; i = ne[i]) {
int j = e[i];
if (j != p) {
if (s.count(((long)u << 32) | j)) cnt0++;
dfs1(j, u);
}
}
}
void dfs2(int u, int p, int cnt) {
// cnt是以u为根的猜对的数量
if (cnt >= k) res++;
// 换根
for (int i = h[u]; i != -1; i = ne[i]) {
int j = e[i];
if (j != p) {
dfs2(j, u, cnt - s.count(((long)u << 32) | j) + s.count(((long)j << 32) | u));
}
}
}
public:
int rootCount(vector<vector<int>>& edges, vector<vector<int>>& guesses, int _k) {
// 建图
memset(h, -1, sizeof h);
for (auto &edge : edges) {
add(edge[0], edge[1]);
add(edge[1], edge[0]);
}
// hash guess数组实现O(1)的询问
for (auto &guesse : guesses) s.insert(((long)guesse[0] << 32 ) | guesse[1]);
dfs1(0, -1);
k = _k;
dfs2(0, -1, cnt0);
return res;
}
};