标签:cnt 并查 puts int cin else 集一 find
-
并查集一
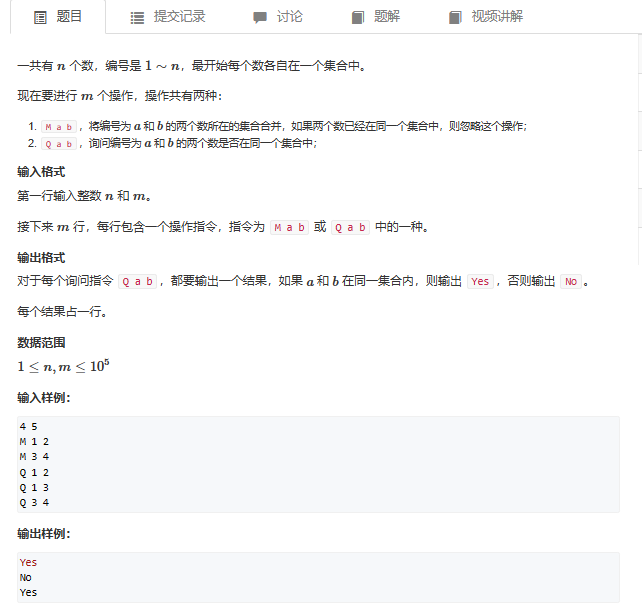
当我们需要快速判断两个元素是否归属于同一个集合
或者将两个集合合并时,就会使用并查集
#include<iostream>
using namespace std;
const int N = 1e5+10;
int p[N];
int n,m;
//寻找祖宗节点,+路径压缩
int find(int x){
if(p[x]!=x) p[x]=find(p[x]);
return p[x];
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++){
p[i]=i;
}
while(m--){
char t;
int a,b;
cin>>t;
if(t=='M'){
cin>>a>>b;
p[find(a)]=find(b);
}
else{
cin>>a>>b;
if(find(a)==find(b)) puts("Yes");
else puts("No");
}
}
return 0;
}

#include<iostream>
using namespace std;
const int N = 100020;
int p[N];
//cnt[find(a)] 维护a所在集合的祖宗节点代表整个连通分支的大小
int cnt[N];
int find(int x){
if(p[x]!=x) p[x]=find(p[x]);
return p[x];
}
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++){
p[i]=i;
cnt[i]=1;
}
while(m--){
string t;
int a,b;
cin>>t;
if(t=="C"){
cin>>a>>b;
//a可能已经和b在一个连通块中了
if(find(a)!=find(b)){
cnt[find(b)]+=cnt[find(a)];
p[find(a)]=find(b);
}else{
continue;
}
}
else if(t=="Q1"){
cin>>a>>b;
if(find(a)==find(b)) puts("Yes");
else puts("No");
}
else{
cin>>a;
cout<<cnt[find(a)]<<endl;
}
}
return 0;
}
标签:cnt,
并查,
puts,
int,
cin,
else,
集一,
find
From: https://www.cnblogs.com/zhouylove/p/17201870.html

