day53

1、leetcode1143 最长公共子序列

1. 动规五部曲

   1. dp[i] [j] = 长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列的长度

      • 下标定义到i-1与j-1 ==》为了简化dp数组第一行和第一列的初始化逻辑

   2. 递推公式

      • 主要就是两大情况： text1[i - 1] 与 text2[j - 1]相同，text1[i - 1] 与 text2[j - 1]不相同
        1. text1[i - 1] == text2[j - 1] ===》说明找到了一个公共元素
           • dp[i] [j] = dp[i-1] [j-1]+1
        2. text1[i - 1] != text2[j - 1] ===》就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列 和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列，取最大的。
           • dp[i] [j] = max(dp[i - 1] [j], dp[i] [j - 1])

   3. 初始化

      • dp[i] [0] = 0 dp[0] [j] = 0

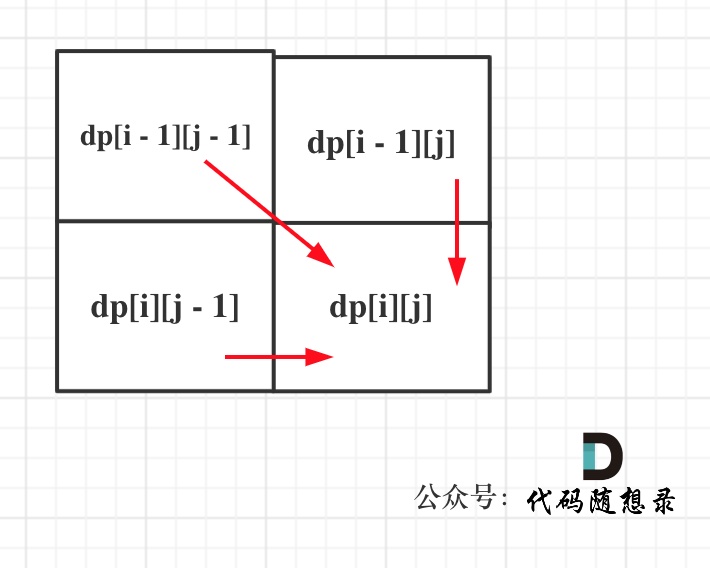
   4. 遍历顺序

      • 从前向后遍历
      • 从上至下遍历

      

   5. 举例

2. 代码

   class Solution {
       public int longestCommonSubsequence(String text1, String text2) {
           int[][] dp = new int[text1.length()+1][text2.length()+1];
   
           for(int i=1; i<=text1.length(); i++) {
               for(int j=1; j<=text2.length(); j++) {
                   if(text1.charAt(i-1) == text2.charAt(j-1)) {
                       dp[i][j] = dp[i-1][j-1]+1;
                   } else {
                       dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]);
                   }
               }
           }
   
           return dp[text1.length()][text2.length()];
       }
   }
   

2、leetcode1035 不相交的线

1. 题目分析

   1. 直线不能相交，这就是说明在数组A中 找到一个与数组B相同的子序列，且这个子序列不能改变相对顺序，只要相对顺序不改变，链接相同数字的直线就不会相交。
   2. 本题说是求绘制的最大连线数，其实就是求两个字符串的最长公共子序列的长度！
   3. 思路同上一题 1143.最长公共子序列

2. 代码

   class Solution {
       public int maxUncrossedLines(int[] nums1, int[] nums2) {
           int[][] dp = new int[nums1.length+1][nums2.length+1];
   
           for(int i=1; i<=nums1.length; i++) {
               for(int j=1; j<=nums2.length; j++) {
                   if(nums1[i-1] == nums2[j-1]) {
                       dp[i][j] = dp[i-1][j-1] + 1;
                   } else {
                       dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]);
                   }
               }
           }
   
           return dp[nums1.length][nums2.length];
       }
   }
   

3、leetcode53 最大子序和

1. 动规五部曲

   1. dp[i] = 以nums[i]结尾的数组的具有最大和的连续子数组的最大和
   2. 递推公式
      • dp[i]只有两个方向可以推出来：
        • dp[i - 1] + nums[i]，即：nums[i]加入当前连续子序列和
        • nums[i]，即：从头开始计算当前连续子序列和
      • 一定是取最大的，所以dp[i] = max(dp[i - 1] + nums[i], nums[i])
   3. 初始化
      • dp[0] = nums[0]
   4. 遍历顺序
      • 从前向后遍历
   5. 举例

   注意：要找最大的连续子序列，就应该找每一个i为终点的连续最大子序列，所以在递推公式的时候，可以直接选出最大的dp[i]。

2. 动规代码

   class Solution {
       public int maxSubArray(int[] nums) {
           int[] dp = new int[nums.length];
           dp[0] = nums[0];
           
           int res = nums[0];
           for(int i=1; i<nums.length; i++) {
               dp[i] = Math.max(dp[i-1] + nums[i], nums[i]);
               res = Math.max(dp[i], res);
           }
   
           return res;
       } 
   }
   

3. 贪心代码

   class Solution {
       public int maxSubArray(int[] nums) {
           int res = Integer.MIN_VALUE;
           int sum = 0;
           
           for(int i=0; i<nums.length; i++) {
               sum += nums[i];
               if(sum > res) {// 取区间累计的最大值（相当于不断确定最大子序终止位置）
                   res = sum;
               }  
               if(sum <= 0) {// 相当于重置最大子序起始位置，因为遇到负数一定是拉低总和
                   sum = 0;
               }
           }
   
           return res;
       }
   }