BZOJ 2870 最长道路
题意
给定一棵 \(n\) 个节点的树,求树上一条链,使得链的长度乘链上所有点中最小权值所得的积最大
\(n\le 5\times 10^4\)
链长度是链上点的个数
做法
首先肯定考虑点分治,考虑所有过重心的链,可以以路径最小值为关键字排序,枚举最小值 \(v\) 并每次从中选出不在同一子树的最大和次大
容易发现不在同一子树这一点比较难以维护(点分治中会把所有节点信息压到一个序列里,在搞不同子树的最小值时就有点难找了),考虑一种解决方法:边分治
边分治
不同于点可以有多个子树的特性,边一定只连了两个节点,也就是切断一条边一定只出现两个不同的子树
所以可以考虑类似点分治的方法对边进行操作,每次只会分出来两棵子树,这一点就容易操作了,把两个序列按从边出发到达这个点的最小值排序,从大到小枚举第一个序列的最小值,记为 \(x\), 在第二个序列中所有最小值 \(\ge x\) 的点中取一条链长最长的,更新答案。枚举第二个序列的最小值类似做
有一个问题在于:考虑一张菊花图,每次取一条边分治时间复杂度会被卡满 \(O(n^2)\) 为了避免这一情况,有一种叫“三度化”的处理方式
容易考虑到上面的情况之所以复杂度过高,是因为同一个节点度数过大,考虑降低节点度数,把树转成一个二叉树
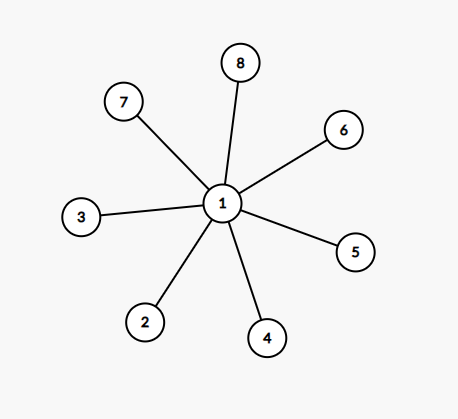
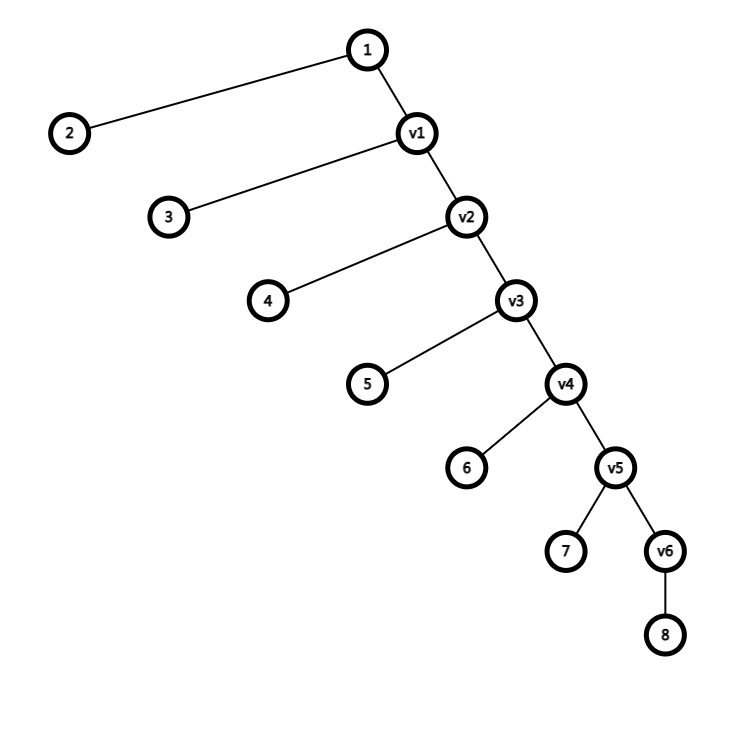
其中,含有了 \(v\) 字符的节点是新增的虚拟节点
通过这样的方式,可以把原树变成一个二叉树,从而保证边分治的复杂度
需要注意的一个事情是,经过一个实点经过虚点和虚边到达另一个实点,实际上等价于经过了他们在原树上的父亲节点——从上面的图中可以看出这一点,需要注意
只要保证新建的虚点和虚边不会影响到答案即可
示例代码如下
#include <iostream>
#include <string.h>
#include <stdio.h>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10, M = 2e5 + 10;
int h[N >> 1], e[M >> 1], ne[M >> 1], idx;
int val[N];
int n;
void add(int x, int y){
e[idx] = y, ne[idx] = h[x], h[x] = idx++;
}
namespace new_tree{
//边的信息
int h[N << 1], e[M << 1], ne[M << 1], w[M << 1], from[M << 1], idx;
int siz[N << 1];
int tt[2];
//某条边有没有用过
bool vis[M << 1];
long long val[N << 1];
//core是边分治选的边
int core, MinMax, NodeNum;
pair<long long, long long> dis[2][N << 1];
long long ans;
//加边
void add(int x, int y, int z){
from[idx] = x, e[idx] = y, ne[idx] = h[x], w[idx] = z, h[x] = idx++;
}
void rebuild(int u, int fa){
//fir 表示当前的虚点
int fir = 0;
val[u] = ::val[u];
for(int i = ::h[u]; ~i; i = ::ne[i]){
int v = ::e[i];
if(v == fa)
continue;
if(!fir){
add(u, v, 1);
add(v, u, 1);
fir = u;
}
else{
//建虚点,连边
int tmp = ++NodeNum;
val[tmp] = val[u];
//虚边上所有点地位等同于这个父节点
//经过任意多同一组虚边所得都等价于经过父节点
add(fir, tmp, 0);
add(tmp, fir, 0);
add(tmp, v, 1);
add(v, tmp, 1);
fir = tmp;
}
rebuild(v, u);
}
}
void DEBUG_PRINT_TREE(int u, int fa){
printf("Node# %d has val: %lld\n", u, val[u]);
printf("Son: ");
for(int i = h[u]; ~i; i = ne[i]){
int v = e[i];
if(v == fa)
continue;
printf("%d ", v);
}
printf("\n");
for(int i = h[u]; ~i; i = ne[i]){
int v = e[i];
if(v == fa)
continue;
DEBUG_PRINT_TREE(v, u);
}
}
void DEBUG_PRINT_EDGE(){
for(int i = 0; i < idx; i++){
printf("From & To: %d %d\n", from[i], e[i]);
}
}
//找到以 u 为根的子树大小
void getsiz(int u, int fa){
siz[u] = 1;
for(int i = h[u]; ~i; i = ne[i]){
int v = e[i];
if(v == fa || vis[i])
continue;
getsiz(v, u);
siz[u] += siz[v];
}
}
//first是从小到大排序的链上最小值
//second是从小到大排序的链长
void getdis(int u, int fa, int d, int stk, int minn){
dis[stk][++tt[stk]].first = minn;
dis[stk][tt[stk]].second = d;
for(int i = h[u]; ~i; i = ne[i]){
int v = e[i];
if(v == fa || vis[i])
continue;
getdis(v, u, d + w[i], stk, min((long long)minn, val[v]));
}
}
void getcore(int u, int tot, int fa){
for(int i = h[u]; ~i; i = ne[i]){
int v = e[i];
if(v == fa || vis[i])
continue;
int subtree = siz[v], fatree = tot - siz[v];
int maxn = max(subtree, fatree);
if(maxn < MinMax){
MinMax = maxn;
core = i;
}
getcore(v, tot, u);
}
}
void work(){
//按最小值的大小从小到大排序
sort(dis[0] + 1, dis[0] + 1 + tt[0]);
sort(dis[1] + 1, dis[1] + 1 + tt[1]);
int i = tt[0], j = tt[1];
long long maxn = 0;
//扫一遍 i
while(i > 0){
//所有最小值大于 i 处最小值的都可以取
while(dis[1][j].first >= dis[0][i].first && j > 0)
maxn = max(maxn, dis[1][j].second), j--;
//分界边被算了两次
//dis[0][i].second + maxn - w[core] 是经过中心边的最长路径长度, 其中还要再加上经过中心节点的
ans = max(ans, dis[0][i].first * (dis[0][i].second + maxn - w[core] + 1));
i--;
}
//扫一遍 j
i = tt[0], j = tt[1];
maxn = 0;
while(j > 0){
while(dis[0][i].first >= dis[1][j].first && i > 0)
maxn = max(maxn, dis[0][i].second), i--;
//分界边被算了两次
ans = max(ans, dis[1][j].first * (dis[1][j].second + maxn + - w[core] + 1));
j--;
}
}
void dfs(int x){
MinMax = NodeNum;
getsiz(x, 0);
getcore(x, siz[x], 0);
int tmp = core;
vis[core] = vis[core ^ 1] = true;
//算出从分界边下去的距离
tt[0] = tt[1] = 0;
getdis(e[core], 0, w[core], 0, val[e[core]]);
getdis(from[core], 0, w[core], 1, val[from[core]]);
int tmp2[2] = {tt[0], tt[1]};
work();
//继续向下DFS的时候core和tt会刷新, 需要暂存
if(tt[1] != 1)
dfs(from[tmp]);
tt[0] = tmp2[0], tt[1] = tmp2[1];
if(tt[0] != 1)
dfs(e[tmp]);
}
void solve(){
NodeNum = ::n;
memset(h, -1, sizeof h);
rebuild(1, 0);
// DEBUG_PRINT_TREE(1, 0);
// DEBUG_PRINT_EDGE();
//初始化dis
dis[1][0] = {0, 0};
dis[0][0] = {0, 0};
dfs(1);
}
}
int main(){
memset(h, -1, sizeof h);
scanf("%d", &n);
for(int i = 1; i <= n; i++){
scanf("%d", &val[i]);
}
for(int i = 1; i < n; i++){
int x, y;
scanf("%d%d", &x, &y);
add(x, y), add(y, x);
}
new_tree::solve();
printf("%lld\n", new_tree::ans);
return 0;
}