DFT
众所周知,我们有离散傅里叶变换:
\[X_k = \sum_{n=0}^{N-1}x_nW_N^{nk} \]而将其值代入自身,就得到:
\[Y_k = \sum_{n=0}^{N-1}X_nW_N^{nk} = \sum_{n=0}^{N-1}\sum_{m=0}^{N-1}x_mW_N^{mn}W_N^{nk} = \sum_{m=0}^{N-1}x_m\sum_{n=0}^{N-1}W_N^{(m+k)n} \]而由 \(W_N\) 的性质,有
\[Y_k=\sum_{m=0}^{N-1}Nx_m[m+k\equiv0\bmod n] \]也就是说,下标在模 \(N\) 意义下,有
\[x_k=\frac{1}{N}Y_{-k}=\frac{1}{N}\sum_{n=0}^{N-1}X_nW_N^{-nk} \]在实现时,可直接 DFT 后翻转区间 \([1,N-1]\) 再对区间 \([0,N-1]\) 除以 \(N\)
FFT
为了快速计算 DFT, 可以分治
DIT - FFT
设 \(y_r = x_{2r}, z_r = x_{2r+1}, M=N/2\)
则有:
\[X_k = \sum_{n=0}^{N-1}x_nW_N^{nk} = \sum_{n=0}^{M-1}y_nW_M^{nk}+W_N^k\sum_{n=0}^{M-1}z_nW_M^{nk} = Y_k+W_N^kZ_k \]\[X_{k+M} = \sum_{n=0}^{N-1}x_nW_N^{n(k+M)} = \sum_{n=0}^{M-1}y_nW_M^{nk}-W_N^k\sum_{n=0}^{M-1}z_nW_M^{nk} = Y_k-W_N^kZ_k \]DIF - FFT
设 \(M=N/2, y_r=x_r+x_{r+M}, z_r=(x_r-x_{r+M})W_N^r\)
则有:
\[X_k = \sum_{n=0}^{N-1}x_nW_N^{nk} = \sum_{n=0}^{M-1}(x_n+(-1)^kx_{n+M})W_N^{nk} \]\[X_{2k} = \sum_{n=0}^{M-1}y_nW_M^{nk} = Y_k, X_{2k+1} = \sum_{n=0}^{M-1}z_nW_M^{nk}=Z_k \]若将计算过程画成一张图,以边权表示乘的系数,则如下:
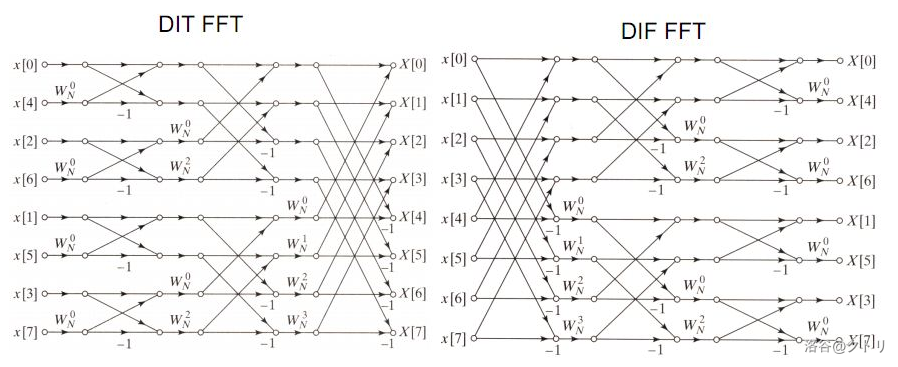
显然,若使用 DIF-FFT 作为 DFT,DIT-FFT 作为 IDFT 可以避免置换
更进一步,若直接按这张图写,\(W_N\) 的变换次数是 \(N+2N/2+4N/4+\cdots=O(n\log n)\) 的,但如果将 DIT-FFT 的以普通数组输入,图会变得和 DIF-FFT 类似,但 \(W_N\) 的变换次数变成了 \(N+N/2+N/4+\cdots=O(N)\)
代码可参考 yhx-12243 的 NTT 究竟写了些什么(详细揭秘)
标签:nk,DFT,sum,FFT,DIT,优化,nW From: https://www.cnblogs.com/JerryTcl/p/17155756.html