力扣题目链接(opens new window)](https://leetcode.cn/problems/balanced-binary-tree/)
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。
示例 1:
给定二叉树 [3,9,20,null,null,15,7]

返回 true 。
示例 2:
给定二叉树 [1,2,2,3,3,null,null,4,4]

返回 false
概念:平衡二叉树
平衡二叉搜索树:又被称为AVL(Adelson-Velsky and Landis)树,且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
如图:
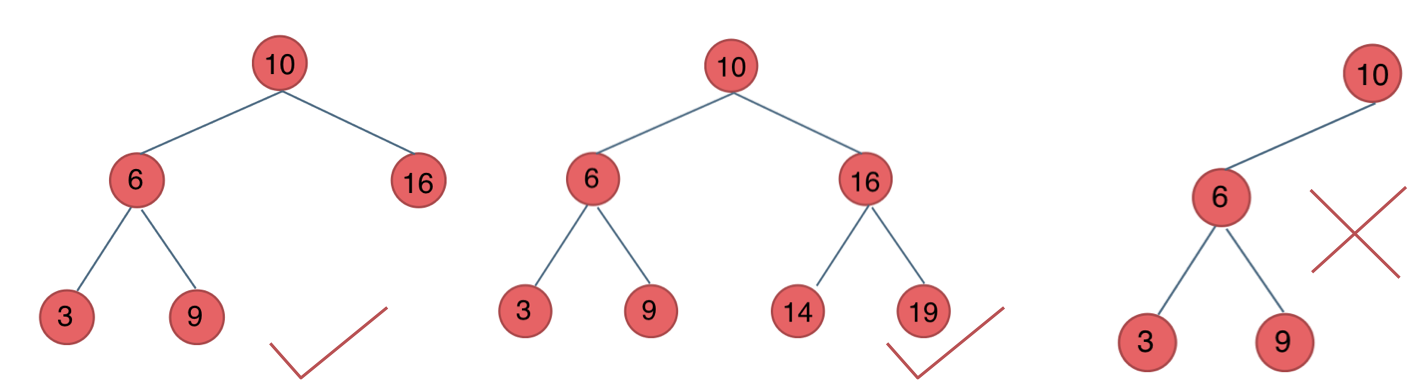
最后一棵 不是平衡二叉树,因为它的左右两个子树的高度差的绝对值超过了1。
C++中map、set、multimap,multiset的底层实现都是平衡二叉搜索树,所以map、set的增删操作时间时间复杂度是logn,注意我这里没有说unordered_map、unordered_set,unordered_map、unordered_set底层实现是哈希表
思路
使用递归回溯的方式解决
既然涉及到了平衡二叉树,那么肯定与去高度计算有关,故需要使用后序遍历来做
因为求深度可以从上到下去查 所以需要前序遍历(中左右),而高度只能从下到上去查,所以只能后序遍历(左右中)
还是递归三部曲:
1、确定递归函数的参数和返回值
一般来说,我们希望:
参数是二叉树当前节点,返回值为以当前节点为根节点计算的高度

举个例子,假设传入节点是2,那么以2为根节点计算的二叉树的高度(红框中的)为3
但是如果当前传入节点为根节点的二叉树已经不是二叉平衡树了,还返回高度的话就没有意义了。
所以如果已经不是二叉平衡树了,可以规定返回-1 来标记已经不符合平衡树的规则了
再来更新一下参数和返回值:
参数是二叉树当前节点,返回值是 -1(不满足平衡二叉树时) 或 以当前节点为根节点计算的高度
// -1 表示已经不是平衡二叉树了,否则返回值是以该节点为根节点树的高度
int getHeight(TreeNode* node)
2、确定终止条件
如果传入的当前节点为空,那么当前树没有高度,递归行为也就应该终止
if (node == NULL) {
return 0;
}
3、明确单层递归逻辑
判断平衡二叉树的依据是当前节点(也就是根节点)的左右子树高度的差值
那么就得分别求出左右子树高度,然后求差值的绝对值,判断是否满足平衡条件
//明确单层处理逻辑
//递归计算当前节点的左子节点的高度
int leftHeight = getHeight(node->left);
//若发现不平衡,返回-1
if(leftHeight == -1)return -1;//左
//递归计算当前节点的左子节点的高度
int rightHeight = getHeight(node->right);
if(rightHeight == -1)return -1;//右
//计算当前节点左右子树的高度差
int res;
if(abs(leftHeight - rightHeight) > 1){//差值大于1,不满足条件
res = -1;
}else{//满足平衡条件,返回以当前节点为根节点的树的最大高度
res = 1 + max(leftHeight, rightHeight);
}
return res;
代码
class Solution {
public:
//确定递归函数参数和返回值
int getHeight(TreeNode* node){
//确定终止条件
if(node == NULL) return 0;
//明确单层处理逻辑
//递归计算当前节点的左子节点的高度
int leftHeight = getHeight(node->left);
//若发现不平衡,返回-1
if(leftHeight == -1)return -1;//左
//递归计算当前节点的左子节点的高度
int rightHeight = getHeight(node->right);
if(rightHeight == -1)return -1;//右
//计算当前节点左右子树的高度差
int res;
if(abs(leftHeight - rightHeight) > 1){//差值大于1,不满足条件
res = -1;
}else{//满足平衡条件,返回以当前节点为根节点的树的最大高度
res = 1 + max(leftHeight, rightHeight);
}
return res;
}
bool isBalanced(TreeNode* root) {
return getHeight(root) == -1 ? false: true;
}
};