参考:bilibili
可并堆
优先队列的缺点:无法高效合并两个堆
左偏树
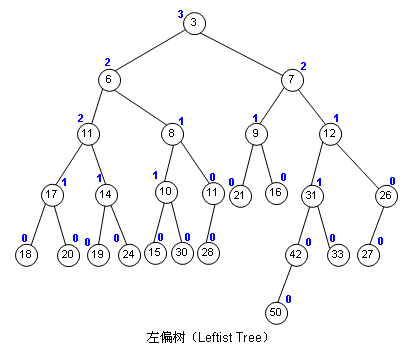
节点中的数字是它的键值,而它是个堆,因此它满足堆的性质:节点的键值小于左右子节点的键值
节点外蓝色数字叫做该节点的距离
- 距离的定义:离该节点最近的“外节点”到该节点的距离
- 外节点:左右儿子不完整的节点
左偏树保证节点的左儿子的距离不小于右儿子的距离
因此可以推出一个节点距离等于右子节点的距离+1
所以空节点的距离为-1
另外,一个N节点的左偏树根节点的距离最大为 \(\log (N+1) -1\)
性质总结
- 小根性质:节点键值小于等于左右儿子的键值
- 左偏性质:节点左儿子的距离不小于其右儿子的距离
- 节点的距离等于其右儿子的距离+1
合并
合并过程中,要维护好左偏树的性质,只要合并后的堆依然满足性质,就合并成功
具体步骤
- 设要合并的两个堆的堆顶节点为 x, y,且 \(val_x \le val_y\)
- 因为小根性质,合并好后的堆的堆顶一定还是 x,所以我们递归合并 x 的儿子(左右都行,一般用右)和 y
- 因为合并完成后可能破坏 x 的左偏性质,所以如果 x 不满足左偏性质了,就交换 x 的左右儿子
- x 的距离有可能变化,利用性质三,令 \(dist_x\) 等于其右儿子的距离 +1
push 与 pop
- push:
和 fhq treap 一样,新建节点然后合并即可
- pop:
合并堆顶节点的两儿子作为新堆顶即可
另外可以把节点的值设为 -1 来标记这个节点被删除了
所以原堆顶的值被设置为 -1 来标记其被删除了
模板题——P3377
- 节点
struct node
{
int l, r, fa;
int val, dis;
}t[N];
- 初始化
t[0].dis = -1;
for(int i = 1; i <= n; i ++ )
{
t[i].val = read();
t[i].fa = i;
}
- 合并
int merge(int x, int y)
{
if(!x || !y) return x + y;
//||前维护小根堆, ||后是题目要求值相同的下标小的优先级高
if(t[x].val > t[y].val || (t[x].val == t[y].val && x > y))
swap(x, y);
t[x].r = merge(t[x].r, y);
t[t[x].r].fa = x;
if(t[t[x].l].dis < t[t[x].r].dis)
swap(t[x].l, t[x].r);
t[x].dis = t[t[x].r].dis + 1;
return x;
}
- 并查集
int find(int x)
{
if(t[x].fa != x) t[x].fa = find(t[x].fa);
return t[x].fa;
}
- 删除堆顶
inline void pop(int x)
{
t[x].val = -1;
t[t[x].l].fa = t[x].l;
t[t[x].r].fa = t[x].r;
t[x].fa = merge(t[x].l, t[x].r);
}
- 完整代码
#define LOCAL
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
inline int read()
{
int x = 0, f = 1;
char ch = getchar();
while(ch < '0' || ch > '9')
{
if(ch == '-') f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9')
{
x = x * 10 + ch - '0';
ch = getchar();
}
return x * f;
}
const int N = 1e5 + 10;
struct node
{
int l, r, fa;
int dis, val;
}t[N];
int merge(int x, int y)
{
if(!x || !y) return x + y;
if(t[x].val > t[y].val || (t[x].val == t[y].val && x > y))
swap(x, y);
t[x].r = merge(t[x].r, y);
t[t[x].r].fa = x;
if(t[t[x].l].dis < t[t[x].r].dis)
swap(t[x].l, t[x].r);
t[x].dis = t[t[x].r].dis + 1;
return x;
}
inline void pop(int x)
{
t[x].val = -1;
t[t[x].l].fa = t[x].l;
t[t[x].r].fa = t[x].r;
t[x].fa = merge(t[x].l, t[x].r);
}
int find(int x)
{
if(t[x].fa != x) t[x].fa = find(t[x].fa);
return t[x].fa;
}
int n, m;
int main()
{
#ifdef LOCAL
freopen("D:\\workspace\\in_and_out\\in.in", "r", stdin);
freopen("D:\\workspace\\in_and_out\\out.out", "w", stdout);
#endif
n = read(), m = read();
t[0].dis = -1;
for(int i = 1; i <= n; i ++ )
{
t[i].val = read();
t[i].fa = i;
}
while(m -- )
{
int op = read(), x = read();
if(op == 1)
{
int y = read();
if(t[x].val == -1 || t[y].val == -1) continue;
int pa = find(x), pb = find(y);
if(pa == pb) continue;
t[pa].fa = t[pb].fa = merge(pa, pb);
}
else
{
if(t[x].val == -1) puts("-1");
else
{
cout << t[find(x)].val << endl;
pop(find(x));
}
}
}
return 0;
}