信息学奥赛一本通 1314：【例3.6】过河卒(Noip2002)

【题目描述】

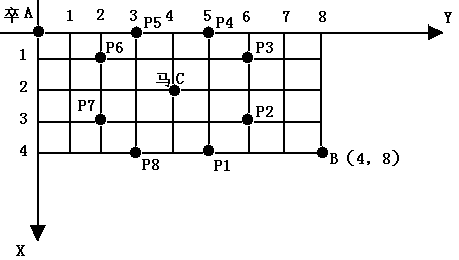
棋盘上A点有一个过河卒，需要走到目标B点。卒行走的规则：可以向下、或者向右。同时在棋盘上的某一点有一个对方的马（如C点），该马所在的点和所有跳跃一步可达的点称为对方马的控制点，如图3-1中的C点和P1，……，P8，卒不能通过对方马的控制点。棋盘用坐标表示，A点(0,0)、B点(n, m) (n,m为不超过20的整数),同样马的位置坐标是需要给出的，C≠A且C≠B。现在要求你计算出卒从A点能够到达B点的路径的条数。

【输入】

给出n、m和C点的坐标。

【输出】

从A点能够到达B点的路径的条数。

【输入样例】

8 6 0 4

【输出样例】

1617

链接：https://pan.baidu.com/s/1gOOOlCqxtPxgusGKya55Ag?pwd=05d3

#include<iostream>
using namespace std;
int n, m, cx, cy;
long long f[40][40], g[40][40];//使用long long避免超出数据范围
int main()
{
    cin>>n>>m>>cx>>cy;
    f[0][0]=1;
    //以下考虑马的控制点有无越界
    g[cx][cy]=1;
    if(cx-1>=0&&cy-2>=0)g[cx-1][cy-2]=1;
    if(cx+1<=n&&cy-2>=0)g[cx+1][cy-2]=1;
    if(cx-2>=0&&cy-1>=0)g[cx-2][cy-1]=1;
    if(cx+2<=n&&cy-1>=0)g[cx+2][cy-1]=1;
    if(cx-2>=0&&cy+1<=m)g[cx-2][cy+1]=1;
    if(cx+2<=n&&cy+1<=m)g[cx+2][cy+1]=1;
    if(cx-1>=0&&cy+2<=m)g[cx-1][cy+2]=1;
    if(cx+1<=n&&cy+2<=m)g[cx+1][cy+2]=1;

    //以下为递推边界
    for(int i=1; i<=n; i++)
        if(!g[i][0])f[i][0]=f[i-1][0];
    for(int j=1; j<=m; j++)
        if(!g[0][j])f[0][j]=f[0][j-1];
    //以下为递推关系式
    for(int i=1; i<=n; i++)
        for(int j=1; j<=m; j++)
        {
            if(g[i][j])f[i][j]=0;
            if(!g[i][j])f[i][j]=f[i][j-1]+f[i-1][j];
        }
    cout<<f[n][m];
    return 0;
}