题目大意:
给你 \(2\times n\) 的迷宫,初始时没有任何障碍,给定 \(q\) 次询问,每次询问给予坐标 \((x,y)\),问将坐标 \((x,y)\) 反转状态(即无障碍变有障碍,有障碍变无障碍)后,该迷宫还能否到达终点 \((2,n)\),并应用更改。
题目分析:
因为是 \(2\times n\) 的迷宫,很显然的是,若下方一个位置为有障碍,则他的左上角或正上方或右上角有障碍时,角色无法到达终点。
同理,对于上方的情况,就是他的左下角或正下方或右下角有障碍时,角色无法到达终点。
如果觉得不大显然的话,可以看下图:
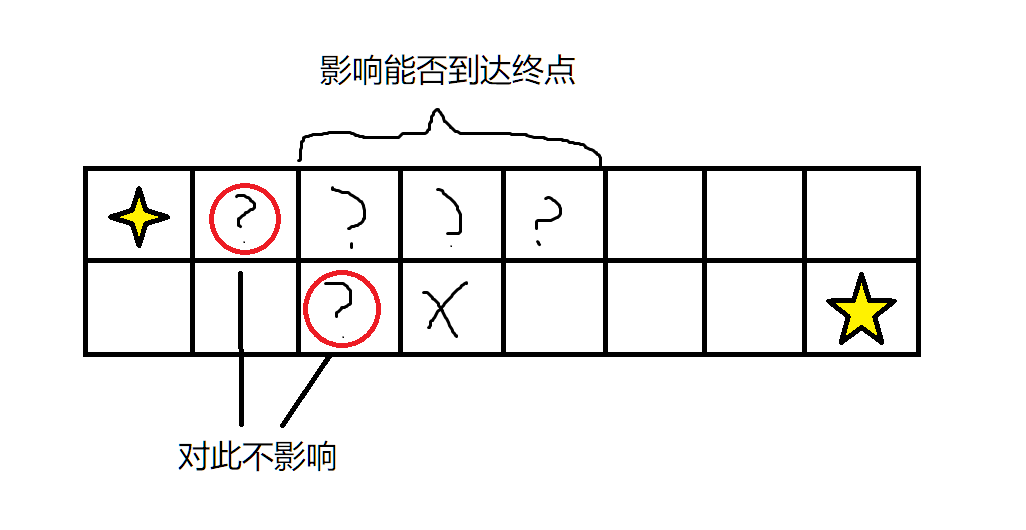
故,我们只需要统计一下形成关联的地方有多少就行了,时间复杂度 \(O(q)\)。
代码实现:
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define TIME_LIMIT (time_t)1.5e3
#define dbg(x) cerr<<#x<<": "<<x<<endl;
#define MAX_SIZE (int)114514
bool bmap[2][MAX_SIZE];
signed main() {
ios::sync_with_stdio(false);
#ifdef LOCAL
freopen("in.in", "r", stdin);
freopen("out.out", "w", stdout);
time_t cs = clock();
#endif
//========================================
int n, q;
cin >> n >> q;
int blocked = 0;
while (q--) {
int x, y;
cin >> x >> y;
x -= 1;
if (x) {
if (bmap[x][y]) {
blocked -= bmap[x - 1][y - 1];
blocked -= bmap[x - 1][y];
blocked -= bmap[x - 1][y + 1];
} else {
blocked += bmap[x - 1][y - 1];
blocked += bmap[x - 1][y];
blocked += bmap[x - 1][y + 1];
}
} else {
if (bmap[x][y]) {
blocked -= bmap[x + 1][y - 1];
blocked -= bmap[x + 1][y];
blocked -= bmap[x + 1][y + 1];
} else {
blocked += bmap[x + 1][y - 1];
blocked += bmap[x + 1][y];
blocked += bmap[x + 1][y + 1];
}
}
bmap[x][y] = !bmap[x][y];
if (blocked)
cout << "No" << endl;
else
cout << "Yes" << endl;
}
//========================================
#ifdef LOCAL
fclose(stdin);
fclose(stdout);
time_t ce = clock();
cerr << "Used Time: " << ce - cs << " ms." << endl;
if (TIME_LIMIT < ce - cs)
cerr << "Warning!! Time exceeded limit!!" << endl;
#endif
return 0;
}