浅析多项式
目录- 浅析多项式
- 更好的阅读体验戳此进入
- 写在前面
- 单位根
- 等比数列求和公式
- FFT
- 例题 #1 LG-P3338 [ZJOI2014]力
- 原根
- NTT
- 例题 #3 LG-P3723 [AH2017/HNOI2017]礼物
- 例题 #4 LG-P4173 残缺的字符串
- 例题 #5 CF528D Fuzzy Search
- 例题 #6 P3321 [SDOI2015]序列统计
- 例题 #7 LG-P4491 [HAOI2018]染色
- 例题 #8 LG-P5395 第二类斯特林数·行
- 例题 #9 LG-P4091 [HEOI2016/TJOI2016]求和
- 例题 #10 LG-P2791 幼儿园篮球题
- 多项式取模
- 多项式求逆
- 例题 #2 LG-P4841 [集训队作业2013]城市规划
- UPD
更好的阅读体验戳此进入
写在前面
关于多项式曾经也写过一篇 Blog,同时亦是我写过的第一篇 Blog,当然可能实际上也没有很理解多项式,所以写的或许比较乱,也可以看一下 FFT & NTT - 快速傅里叶变换 & 快速数论变换。
单位根
定义
对于 $ \omega^n = 1 (\omega \neq 1)$,称 $ \omega $ 为 $ n $ 次单位根,其可以为模意义下的或复数意义下的。
复数意义下的的求法
考虑将单位圆 $ n $ 等分,并取这 $ n $ 个点对应的素数,从 $ x $ 轴,即 $ (1, 0) $ 开始取,逆时针从 $ 0 $ 开始编号,对于第 $ k $ 个复数记作 $ \omega_n^k $。所以以下结论显然:
对于幅角为 $ 0 $ 的最小复数 $ \omega_n^1 $,由复数乘法规则可知 $ (\omega_n1)k = \omega_n^k $,所以 $ (\omega_n1)n = \omega_n^n = \omega_n^0 = 1 $,则显然 $ \omega_n^1 $ 为复数意义下的 $ n $ 次单位根。
则显然对于 $ n $ 次单位根的 $ k $ 次方,用高中知识转换为三角函数即可,即:
\[\omega_n^k = \cos(\dfrac{2\pi}{n} \times k) + \sin(\dfrac{2\pi}{n} \times k)i \]性质
复数意义下的单位根,易证有如下性质:
性质一:
\[\omega_n^k = \omega_{an}^{ak} \]性质二:
\[\omega_n^{k + \tfrac{n}{2}} = -\omega_n^k \]等比数列求和公式
没什么可说的,公比为 $ q $,则有下式。详细证明。
\[S_n = a_1 \dfrac{1-q^n}{1-q} \]FFT
本质
在我的理解里,FFT 的本质就是将多项式的系数表示法转换为点值表示法,然后进行快速处理,再转换为一般的系数表示法。
因为显然朴素的多项式乘法为 $ O(n^2) $ 的,而点值表示法的多项式乘法是 $ O(n) $ 的,所以我们需要将朴素的 $ O(n^2) $ 的系数与点值转换过程优化为 $ O(n \log n) $ 的。
目的
显然目的就是求两个多项式的卷积,我们定义 $ A(x), B(x), C(x) $ 为多项式,$ a(x), b(x), c(x) $ 为多项式的对应系数。即 $ C(x) = A(x) \ast B(x) $,或者表示为:
\[c(i) = \sum_{j = 0}^ia(j) \times b(i - j) \]离散傅里叶变换
考虑我们前文提过的单位根,首先我们将 $ \omega_n^0, \omega_n1,\omega_n2, \cdots, \omega_n^{n - 1} $ 代入多项式的点值表示称作离散傅里叶变换。
关于为什么一定要选择这些值,在我以前写的里面的推式子有些繁琐,当然也可以证明。这里参考一下网上的另一种更简洁的方法。
首先我们记 $ (y_0, y_1, y_2, \cdots, y_{n - 1}) $ 为多项式 $ A(x) = \sum_{i = 0}^{n - 1}a_ix^i $ 的离散傅里叶变换。然后令多项式 $ B(x) = \sum_{i = 0}^{n - 1}y_ix^i $,然后这里我们用所有单位根 $ k $ 次方的倒数,也就是对应的共轭复数,带入 $ B(x) $,即带入 $ \omega_n^0, \omega_n{-1},\omega_n, \cdots, \omega_n^{-n + 1} $,得到一个新的 “离散傅里叶变换”,记作 $ (z_0, z_1, z_2,.\cdots, z_{n - 1}) $,则有:
\[\begin{aligned} z_k &= \sum_{i = 0}^{n - 1}y_i(\omega_n^{-k})^i \\ &= \sum_{i = 0}^{n - 1} (\sum_{j = 0}^{n - 1}a_j(\omega_n^i)^j) (\omega_n^{-k})^i \\ &= \sum_{j = 0}^{n - 1} a_j (\sum_{i = 0}^{n - 1}(\omega_n^{j - k})^i) \end{aligned} \]然后对于 $ \sum_{i = 0}^{n - 1}(\omega_n^{j - k})^i $,显然 $ j = k $ 的时候该式为 $ n $,反之通过等比数列求和公式易证其为 $ 0 $,则显然有 $ z_k = n \times a_k $,所以有:
\[a_i = \dfrac{z_i}{n} \]所以不难发现,我们转为系数表示法之后,即 DFT 过程之后,对于得到的离散傅里叶变换结果,再次当作一个新的多项式的系数以单位根倒数再跑一遍转换系数表示法的过程,即 IDFT,然后将每个数的实数部分除以 $ n $,最终得到的就是我们想要的结果
所以现在我们就需要优化 $ O(n^2) $ 的转化过程了。
快速傅里叶变换
首先仍考虑一个一般的多项式:
\[A(x) = \sum_{i = 0}^{n - 1}a_ix^i \]我们按照下标的奇偶性分类,则有如下两个多项式:
\[\begin{aligned} A_1(x) = a_0 + a_2x + \cdots + a_{n - 2}x^{\tfrac{n}{2} - 1} \\ A_2(x) = a_1 + a_3x + \cdots + a_{n - 1}x^{\tfrac{n}{2} - 1} \end{aligned} \]然后不难发现有:
\[A(x) = A_1(x^2) + xA_2(x^2) \]然后考虑对于 $ k \lt \dfrac{n}{2} $ 的部分,带入 $ \omega_n^k $,有:
\[\begin{aligned} A(\omega_n^k) &= A_1(\omega_n^{2k}) + \omega_n^kA_2(\omega_n^{2k}) \\ &= A_1(\omega_{\tfrac{n}{2}}^{k}) + \omega_n^kA_2(\omega_{\tfrac{n}{2}}^{k}) \end{aligned} \]然后对于 $ \ge \dfrac{n}{2} $ 的部分,考虑带入 $ \omega_n^{k + \tfrac{n}{2}} $:
\[\begin{aligned} A(\omega_n^{k + \tfrac{n}{2}}) &= A_1(\omega_n^{2k + n}) + \omega_n^{k + \tfrac{n}{2}}A_2(\omega_n^{2k + n}) \\ &= A_1(\omega_{\tfrac{n}{2}}^{k} \omega_{n}^{n}) + \omega_n^{k + \tfrac{n}{2}}A_2(\omega_{\tfrac{n}{2}}^{k} \omega_{n}^{n}) \\ &= A_1(\omega_{\tfrac{n}{2}}^{k}) - \omega_n^{k}A_2(\omega_{\tfrac{n}{2}}^{k}) \end{aligned} \]此时发现问题规模减半,合并是 $ O(n) $ 的,即:
\[T(n) = T(\dfrac{n}{2}) + O(n) \]则由主定理可知复杂度为 $ O(n \log n) $。
Tips:同时需要注意,上文即下文所用的长度 $ n $ 若无特殊限制则均应保证满足 $ n = 2^t $,若不满足可在最后添加 $ 0 $ 直至满足。
优化
这样虽然就可以实现 FFT 了,但是它是不优雅的,我们可以将递归改为非递归实现。
考虑 Cooley-Tukey 算法,首先有以下递归的例子:(图片来自 一小时学会快速傅里叶变换(Fast Fourier Transform))
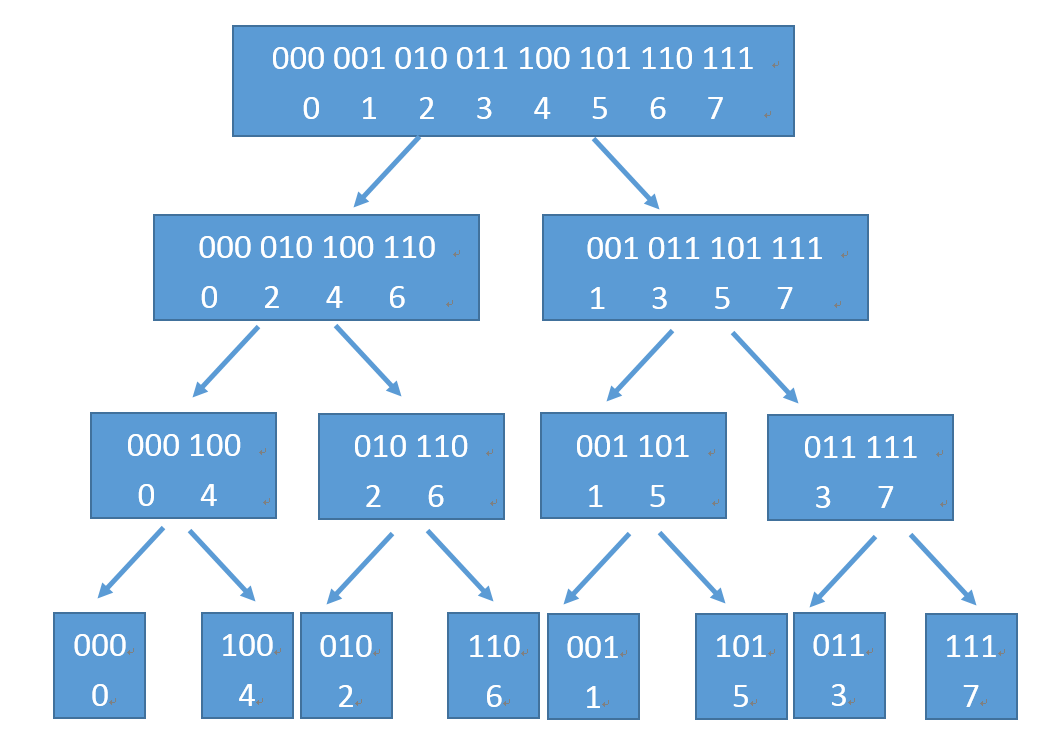
不难发现,每个位置变化的数即为将其二进制下的所有数反转,如 $ 1 $ 从 $ 001 $ 变为 $ 110 $。于是可以据此进行非递归优化。
首先朴素的模拟这个反转的过程应该是 $ O(n \log n) $ 的,不够优秀,仍存在如下写法:
int pos[len + 10];
memset(pos, 0, sizeof(pos));
for(int i = 0; i < len; ++i){
pos[i] = pos[i >> 1] >> 1;
if(i & 1)pos[i] |= len >> 1;
}
for(int i = 0; i < len; ++i)if(i < pos[i])swap(pol[i], pol[pos[i]]);
不难发现这个的复杂度是线性的,严谨证明略,可以尝试通过举个例子来理解:
假设我们有一个二进制数 $ 0101110 $ 我们想要对其进行 Reverse,因为我们要进行递推,所以需要分解为子问题,可以考虑将其右移一位,即变为 $ 0010111 $,然后 Reverse,变为 $ 1110100 $,在对比我们想要求得的 $ 0111010 $,发现前者去掉最后一位,后者忽略第一位是完全相同的,那么将前者右移一位后在考虑最前面一位是 $ 1 $ 还是 $ 0 $ 即可。
此时则可以在过程中不进行递归,而从下至上地取合并,不难想到枚举长度后再枚举每个起点即可。
对于朴素的 FFT 提供如下实现:(以前写的代码,可能实现不是很精细)
对应题目:P3803 【模板】多项式乘法(FFT)。
Code
#define _USE_MATH_DEFINES
#include <bits/stdc++.h>
#include <mmintrin.h>
#define PI M_PI
#define E M_E
#define DFT true
#define IDFT false
#define eps 1e-6
#define comp complex < double >
/******************************
abbr
pat -> pattern
pol/poly -> polynomial
omg -> omega
******************************/
using namespace std;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
class Polynomial{
private:
int lena, lenb;
int len;
comp A[2100000], B[2100000];
public:
comp Omega(int, int, bool);
void Init(void);
void FFT(comp*, int, bool);
void Reverse(comp*);
void MakeFFT(void);
}poly;
template<typename T = int>
inline T read(void);
int main(){
poly.Init();
poly.MakeFFT();
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
void Polynomial::MakeFFT(void){
FFT(A, len, DFT), FFT(B, len, DFT);
for(int i = 0; i <= len; ++i)A[i] *= B[i];
FFT(A, len, IDFT);
for(int i = 0; i <= lena + lenb - 2; ++i)
printf("%d%c", int(A[i].real() / len + eps + 0.5), i == lena + lenb - 2 ? '\n' : ' ');
}
void Polynomial::Reverse(comp* pol){
int pos[len + 10];
memset(pos, 0, sizeof(pos));
for(int i = 0; i < len; ++i){
pos[i] = pos[i >> 1] >> 1;
if(i & 1)pos[i] |= len >> 1;
}
for(int i = 0; i < len; ++i)if(i < pos[i])swap(pol[i], pol[pos[i]]);
}
void Polynomial::FFT(comp* pol, int len, bool pat){
Reverse(pol);
for(int size = 2; size <= len; size <<= 1){
for(comp* p = pol; p != pol + len; p += size){
int mid(size >> 1);
for(int i = 0; i < mid; ++i){
auto tmp = Omega(size, i, pat) * p[i + mid];
p[i + mid] = p[i] - tmp;
p[i] = p[i] + tmp;
}
}
}
}
void Polynomial::Init(void){
lena = read(), lenb = read();
for(int i = 0; i <= lena; ++i)A[i].real((double)read());
for(int i = 0; i <= lenb; ++i)B[i].real((double)read());
len = 1;
lena++, lenb++;
while(len <= lena + lenb)len <<= 1;
}
comp Polynomial::Omega(int n, int k, bool pat){
if(pat == DFT)return comp(cos(2 * PI * k / n), sin(2 * PI * k / n));
return conj(comp(cos(2 * PI * k / n), sin(2 * PI * k / n)));
}
template<typename T>
inline T read(void){
T ret(0);
int flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
例题 #1 LG-P3338 [ZJOI2014]力
题面
令:
\[E_i = \sum_{j = 1}^{i - 1}\dfrac{q_j}{(i - j)^2} - \sum_{j = i + 1}^n \dfrac{q_j}{(i - j)^2} \]求 $ \forall i \in [1, n], E_i $。
Solution
令 $ x_i = \dfrac{1}{i^2} $,原式转化为:
\[E_i = \sum_{j = 1}^{i - 1}q_jx_{i - j} - \sum_{j = i + 1}^n q_jx_{j - i} \]令 $ r_i = q_{n - i + 1} $,则可再次转化:
\[E_i = \sum_{j = 1}^{i - 1}q_jx_{i - j} - \sum_{j = i + 1}^{n} r_{n - j + 1}x_{j - i} \]等价于:
\[E_i = \sum_{j = 1}^{i - 1}q_jx_{i - j} - \sum_{j = 1}^{n - i} r_{j}x_{n - i - j + 1} \]令 $ q_0 = r_0 = x_0 = 0 $,则亦等价于:
\[E_i = \sum_{j = 0}^{i}q_jx_{i - j} - \sum_{j = 0}^{n - i + 1} r_{j}x_{n - i - j + 1} \]发现前者后者均满足卷积形式,使用 FFT 优化即可。
Code
#define _USE_MATH_DEFINES
#include <bits/stdc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW void* Edge::operator new(size_t){static Edge* P = ed; return P++;}
#define ROPNEW_NODE void* Node::operator new(size_t){static Node* P = nd; return P++;}
using namespace std;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
#define DFT (true)
#define IDFT (false)
#define comp complex < ld >
template < typename T = int >
inline T read(void);
int N;
ld Q[410000];
comp Omega(int n, int k, bool pat){
if(pat)return comp(cos(2 * PI / n * k), sin(2 * PI / n * k));
return conj(comp(cos(2 * PI / n * k), sin(2 * PI / n * k)));
}
class Polynomial{
private:
public:
int len;
comp poly[410000];
int pos[410000];
Polynomial(void){
len = 0;
memset(poly, 0, sizeof poly);
memset(pos, 0, sizeof pos);
}
void Reverse(void){
for(int i = 0; i < len; ++i){
pos[i] = pos[i >> 1] >> 1;
if(i & 1)pos[i] |= len >> 1;
}
for(int i = 0; i < len; ++i)if(i < pos[i])swap(poly[i], poly[pos[i]]);
}
void FFT(bool pat){
Reverse();
for(int siz = 2; siz <= len; siz <<= 1)
for(auto p = poly; p != poly + len; p += siz){
int mid(siz >> 1);
for(int i = 0; i < mid; ++i){
auto tmp = Omega(siz, i, pat) * p[i + mid];
p[i + mid] = p[i] - tmp;
p[i] = p[i] + tmp;
}
}
}
auto operator *= (Polynomial P){
int rlen = len + P.len - 1;
int base(1);
while(base < rlen)base <<= 1;
len = P.len = base;
FFT(DFT), P.FFT(DFT);
for(int i = 0; i < len; ++i)poly[i] *= P.poly[i];
FFT(IDFT);
for(int i = 0; i < len; ++i)poly[i] /= len;
}
};
int main(){
N = read();
for(int i = 1; i <= N; ++i)scanf("%Lf", Q + i);
++N;
Polynomial q, r, x;
int base(1); while(base < N)base <<= 1;
q.len = r.len = x.len = base;
--N;
for(int i = 1; i <= N; ++i)q.poly[i].real(Q[i]), r.poly[i].real(Q[N - i + 1]), x.poly[i].real((ld)1.0 / (ld)i / (ld)i);
q *= x, r *= x;
for(int i = 1; i <= N; ++i)printf("%.3Lf\n", q.poly[i].real() - r.poly[N - i + 1].real());
// Polynomial A, B;
// A.len = B.len = 2;
// A.poly[1].real(114.0), B.poly[1].real(514.0);
// A *= B;
// for(int i = 0; i <= 5; ++i)printf("poly[%d] = %.8Lf\n", i, A.poly[i].real());
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template < typename T >
inline T read(void){
T ret(0);
int flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
原根
详细定义可参考 知乎 或 OI-WIKI,简而言之就是,对于模 $ P $ 意义下的原根 $ g $,有 $ g^1, g^2, \cdots, g^{P - 2} \bmod m $ 的值各不相同。
NTT
中文全称快速数论变换,和快速傅里叶变换的区别就是前者在模意义下,后者在复数意义下。
而可以证明,模意义下的可以通过原根代替单位根,特别地,假设存在模 $ P $ 意义下的原根 $ g $,若满足 $ n \mid P - 1 $,则令:
\[g_n^k = (g^{\tfrac{P - 1}{n}})^k \]我们只需要验证 $ g_n^k $ 满足单位根需要的几个性质即可。
显然 $ g_n^n = g^{P - 1} $ ,且 $ g_{an}^{ak} = (g^\tfrac{P - 1}{an})^{ak} = g_n^k $,且 $ g_n^0 = 1 $ 显然成立。
然后由于 $ g \bot P $ 且若 $ P $ 为质数,则根据欧拉定理可知 $ g^{P - 1} \equiv 1 \pmod{P} $ 则显然 $ g_n^{k + \tfrac{n}{2}} = g_{2n}^{2k + n} = g_{2n}^{2k} \times g_n^n = g_{2n}^{2k} \times g^{P - 1} = g_{2n}^{2k} = g_{n}^{k} $。
故可以直接用 $ g_n^k $ 代替 $ \omega_n^k $。
对于单位根的倒数,在 FFT 中通过共轭复数实现,这里我们便通过乘法逆元实现。
本质上并无太大区别,这里同样提供一个实现:(以前写的代码,可能实现不够精细)
对应题目:P3803 【模板】多项式乘法(FFT)。
Code
#define _USE_MATH_DEFINES
#include <bits/stdc++.h>
#include <mmintrin.h>
#define PI M_PI
#define E M_E
#define DFT true
#define IDFT false
#define eps 1e-6
#define MOD 998244353
/******************************
abbr
pat -> pattern
pol/poly -> polynomial
omg -> omega
******************************/
using namespace std;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
ll kpow(int a, int b){
ll ret(1ll), mul((ll)a);
while(b){
if(b & 1)ret = (ret * mul) % MOD;
b >>= 1;
mul = (mul * mul) % MOD;
}
return ret;
}
class Polynomial{
private:
int lena, lenb;
int len;
int g, inv_g;
int A[2100000], B[2100000];
public:
int Omega(int, int, bool);
void Init(void);
void NTT(int*, int, bool);
void Reverse(int*);
void MakeNTT(void);
}poly;
template<typename T = int>
inline T read(void);
int main(){
// freopen("P3803_4.in", "r", stdin);
poly.Init();
poly.MakeNTT();
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
void Polynomial::MakeNTT(void){
NTT(A, len, DFT), NTT(B, len, DFT);
for(int i = 0; i <= len; ++i)A[i] = ((ll)A[i] * B[i]) % MOD;
NTT(A, len, IDFT);
int mul_inv = kpow(len, MOD - 2);
for(int i = 0; i <= lena + lenb - 2; ++i)
printf("%d%c", (ll)A[i] * mul_inv % MOD, i == lena + lenb - 2 ? '\n' : ' ');
}
void Polynomial::Reverse(int* pol){
int pos[len + 10];
memset(pos, 0, sizeof(pos));
for(int i = 0; i < len; ++i){
pos[i] = pos[i >> 1] >> 1;
if(i & 1)pos[i] |= len >> 1;
}
for(int i = 0; i < len; ++i)if(i < pos[i])swap(pol[i], pol[pos[i]]);
}
void Polynomial::NTT(int* pol, int len, bool pat){
Reverse(pol);
for(int size = 2; size <= len; size <<= 1){
int gn = kpow(pat == DFT ? g : inv_g, (MOD - 1) / size);
for(int* p = pol; p != pol + len; p += size){
int mid(size >> 1);
int g(1);
for(int i = 0; i < mid; ++i, g = ((ll)g * gn) % MOD){
auto tmp = ((ll)g * p[i + mid]) % MOD;
p[i + mid] = (p[i] - tmp + MOD) % MOD;
p[i] = (p[i] + tmp) % MOD;
}
}
}
}
void Polynomial::Init(void){
lena = read(), lenb = read();
for(int i = 0; i <= lena; ++i)A[i] = read();
for(int i = 0; i <= lenb; ++i)B[i] = read();
len = 1;
lena++, lenb++;
while(len < lena + lenb)len <<= 1;
g = 3;
inv_g = kpow(g, MOD - 2);
}
template<typename T>
inline T read(void){
T ret(0);
short flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
例题 #3 LG-P3723 [AH2017/HNOI2017]礼物
题面
存在两个有点权的环,可以对其中任意一个中的所有权值加上一个任意的非负整数,且可以任意旋转环,最小化 $ \sum_{i = 1}^n (x_i - y_i)^2 $,输出最小值。
Solution
任意一个加上非负整数可以转换为在其中某一个加上整数,显然该整数符合绝对值不大于 $ 100 $,于是可以考虑枚举增加的 $ c $,此时答案为:
\[\sum_{i = 1}^n (x_i + c - y_i)^2 = \sum_{i = 1}^n x_i^2 + c^2 + y_i^2 + 2cx_i - 2cy_i - 2x_iy_i \]显然除了 $ \sum 2x_iy_i $ 均为定值,于是考虑求 $ \sum x_iy_i $ 的最大值即可。这东西有点像卷积,于是想到翻转 $ y $,并倍长一份 $ x $,令 $ F(i) $ 表示旋转 $ i $ 之后的值,有:
\[F(i) = \sum_{j = 1}^{n} x_{j + i}y_{n - j + 1} \]NTT 优化一下即可。
#define _USE_MATH_DEFINES
#include <bits/stdc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW void* Edge::operator new(size_t){static Edge* P = ed; return P++;}
#define ROPNEW_NODE void* Node::operator new(size_t){static Node* P = nd; return P++;}
using namespace std;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
#define DFT (true)
#define IDFT (false)
#define MOD (998244353ll)
template < typename T = int >
inline T read(void);
int N, M;
int X[51000], Y[51000];
int pos[610000];
ll g(3), inv_g;
ll ans(0), sumX(0), sumY(0);
ll qpow(ll a, ll b){
ll ret(1), mul(a);
while(b){
if(b & 1)ret = ret * mul % MOD;
b >>= 1;
mul = mul * mul % MOD;
}return ret;
}
class Polynomial{
private:
public:
int len;
ll poly[610000];
Polynomial(void){
len = 0;
memset(poly, 0, sizeof poly);
}
void Reverse(void){
memset(pos, 0, sizeof(ll) * (len + 10));
for(int i = 0; i < len; ++i)
pos[i] = (pos[i >> 1] >> 1) | (i & 1 ? len >> 1 : 0);
for(int i = 0; i < len; ++i)if(i < pos[i])swap(poly[i], poly[pos[i]]);
}
void NTT(bool pat){
Reverse();
for(int siz = 2; siz <= len; siz <<= 1){
ll gn = qpow(pat ? g : inv_g, (MOD - 1) / siz);
for(auto p = poly; p != poly + len; p += siz){
int mid(siz >> 1); ll g(1);
for(int i = 0; i < mid; ++i, (g *= gn) %= MOD){
auto tmp = g * p[i + mid] % MOD;
p[i + mid] = (p[i] - tmp + MOD) % MOD;
p[i] = (p[i] + tmp) % MOD;
}
}
}
if(!pat){
ll inv_len = qpow(len, MOD - 2);
for(int i = 0; i < len; ++i)(poly[i] *= inv_len) %= MOD;
}
}
};
int main(){
inv_g = qpow(g, MOD - 2);
N = read(), M = read();
for(int i = 1; i <= N; ++i)X[i] = read(), ans += X[i] * X[i], sumX += 2 * X[i];
for(int i = 1; i <= N; ++i)Y[N - i + 1] = read(), ans += Y[N - i + 1] * Y[N - i + 1], sumY += 2 * Y[N - i + 1];
Polynomial A, B;
for(int i = 1; i <= N; ++i)A.poly[i] = A.poly[i + N] = X[i], B.poly[i] = Y[i];
A.len = N * 2 + 1, B.len = N + 1;
int clen = A.len + B.len - 1, base(1);
while(base < clen)base <<= 1;
A.len = B.len = base;
A.NTT(DFT), B.NTT(DFT);
for(int i = 0; i < A.len; ++i)A.poly[i] = A.poly[i] * B.poly[i] % MOD;
A.NTT(IDFT);
ll mx(-1);
for(int i = 0; i < A.len; ++i)mx = max(mx, A.poly[N + i]);
ans -= 2 * mx;
ll mn(LONG_LONG_MAX);
for(ll c = -100; c <= 100; ++c)
mn = min(mn, N * c * c + c * sumX - c * sumY);
ans += mn;
printf("%lld\n", ans);
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template < typename T >
inline T read(void){
T ret(0);
int flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
例题 #4 LG-P4173 残缺的字符串
题面
带通配符的单模式串匹配。
Solution
首先考虑不使用 KMP 的情况下的高效的无通配符的单模式串匹配。
考虑定义匹配函数 $ C(x, y) = A(x) - B(y) $,即若 $ C(x, y) = 0 $ 那么 $ A, B $ 对应位置的字符匹配。
继续考虑定义完全匹配函数,假设模式串为 $ A $,模式串长度为 $ m $,则有完全匹配函数:
\[P(x) = \sum_{i = 0}^{m - 1}C(i, x - m + i + 1) \]则若 $ P(x) = 0 $,说明 $ B $ 的以 $ x $ 为结尾的连续 $ m $ 位与模式串匹配。
但是存在问题,即 ab 与 ba 错误地匹配了。但是绝对值难以优化,于是考虑进行平方,即令完全匹配函数为:
考虑将 $ A $ 翻转后,则有:
\[P(x) = \sum_{i = 0}^{m - 1}(A(m - i - 1) - B(x - m + i + 1))^2 \]将其展开后不难发现,前几项可以在优秀的复杂度内求出,最后一项可以用多项式优化。
考虑存在通配符的情况,令通配符对应值为 $ 0 $,则定义匹配函数:
\[C(x, y) = (A(x) - B(y))^2A(x)B(y) \]此时依然以此定义完全匹配函数,并对 $ A $ 进行翻转,有:
\[P(x) = \sum_{i = 0}^{m - 1} (A(m - i - 1) - B(x - m + i + 1))^2A(m - i - 1)B(x - m + i + 1) \]我们考虑从意义上去进行简化,即不难发现枚举的 $ m - i - 1 $ 和 $ x - m + i + 1 $ 对应的实际上就是枚举 $ i $ 并枚举 $ x - i $,于是将上式完全展开后并化简,得到:
\[P(x) = \sum_{i = 0}^{x}A(i)^3B(x - i) + \sum_{i = 0}^{x}A(i)B(x - i)^3 - \sum_{i = 0}^{x}2A(i)^2B(x - i)^2 \]不难发现这就是三个卷积形式,直接用 FFTNTT 优化即可。
同时有个细节记得注意,这里是两个多项式相乘,而不是四个多项式,对于 $ A(i)^3 $ 代表的是一个多项式。
然后用 FFT 的话硬卡常应该也能过,可能需要手写复数之类的一系列操作,懒得弄了就换成 NTT 了,速度瞬间快了几倍。
Code
#define _USE_MATH_DEFINES
#include <bits/stdc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW void* Edge::operator new(size_t){static Edge* P = ed; return P++;}
#define ROPNEW_NODE void* Node::operator new(size_t){static Node* P = nd; return P++;}
using namespace std;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
#define DFT (true)
#define IDFT (false)
// #define comp complex < ld >
#define comp complex < double >
#define MOD (998244353ll)
template < typename T = int >
inline T read(void);
int M, N;
int pos[1300000];
string S1, S2;
int A[1300000], B[1300000];
ll g(3), inv_g;
// comp Omega(int n, int k, bool pat){
// if(pat)return comp(cos(2 * PI / n * k), sin(2 * PI / n * k));
// return conj(comp(cos(2 * PI / n * k), sin(2 * PI / n * k)));
// }
ll qpow(ll a, ll b){
ll ret(1), mul(a);
while(b){
if(b & 1)ret = ret * mul % MOD;
b >>= 1;
mul = mul * mul % MOD;
}return ret;
}
class Polynomial{
private:
public:
int len;
ll poly[1300000];
Polynomial(void){
len = 0;
memset(poly, 0, sizeof poly);
}
void Reverse(void){
memset(pos, 0, sizeof(int) * (len + 10));
for(int i = 0; i < len; ++i)
pos[i] = (pos[i >> 1] >> 1) | (i & 1 ? len >> 1 : 0);
for(int i = 0; i < len; ++i)if(i < pos[i])swap(poly[i], poly[pos[i]]);
}
void FFT(bool pat){
Reverse();
for(int siz = 2; siz <= len; siz <<= 1){
ll gn = qpow(pat ? g : inv_g, (MOD - 1) / siz);
for(auto p = poly; p != poly + len; p += siz){
int mid = siz >> 1; ll g(1);
for(int i = 0; i < mid; ++i, (g *= gn) %= MOD){
auto tmp = g * p[i + mid] % MOD;
p[i + mid] = (p[i] - tmp + MOD) % MOD;
p[i] = (p[i] + tmp) % MOD;
}
}
}
if(!pat){
// for(int i = 0; i < len; ++i)poly[i].real(poly[i].real() / len);
ll inv_len = qpow(len, MOD - 2);
for(int i = 0; i < len; ++i)(poly[i] *= inv_len) %= MOD;
}
}
void Print(void){
// printf("Polynomial(len = %d): ", len);
// for(int i = 0; i < len; ++i)printf("%.3lf ", poly[i].real());
// printf("\n");
}
};
int main(){
inv_g = qpow(g, MOD - 2);
// ios::sync_with_stdio(false);
M = read(), N = read();
// cin >> M >> N;
cin >> S1 >> S2;
reverse(S1.begin(), S1.end());
for(int i = 0; i < M; ++i)A[i] = S1.at(i) == '*' ? 0 : S1.at(i) - 'a' + 1;
for(int i = 0; i < N; ++i)B[i] = S2.at(i) == '*' ? 0 : S2.at(i) - 'a' + 1;
Polynomial P, PA, PB;
int clen = N + M - 1, base(1);
while(base < clen)base <<= 1;
P.len = PA.len = PB.len = base;
// for(int i = 0; i < base; ++i)PA.poly[i].real(A[i] * A[i] * A[i]), PA.poly[i].imag(0);
// for(int i = 0; i < base; ++i)PB.poly[i].real(B[i]), PB.poly[i].imag(0);
for(int i = 0; i < base; ++i)PA.poly[i] = A[i] * A[i] * A[i], PB.poly[i] = B[i];
PA.FFT(DFT), PB.FFT(DFT);
for(int i = 0; i < base; ++i)P.poly[i] += PA.poly[i] * PB.poly[i];
// memset(PA.poly, 0, sizeof PA.poly), memset(PB.poly, 0, sizeof PB.poly);
// for(int i = 0; i < base; ++i)PA.poly[i].real(A[i]), PA.poly[i].imag(0);
// for(int i = 0; i < base; ++i)PB.poly[i].real(B[i] * B[i] * B[i]), PB.poly[i].imag(0);
for(int i = 0; i < base; ++i)PA.poly[i] = A[i], PB.poly[i] = B[i] * B[i] * B[i];
PA.FFT(DFT), PB.FFT(DFT);
for(int i = 0; i < base; ++i)P.poly[i] += PA.poly[i] * PB.poly[i];
// memset(PA.poly, 0, sizeof PA.poly), memset(PB.poly, 0, sizeof PB.poly);
// for(int i = 0; i < base; ++i)PA.poly[i].real(A[i] * A[i]), PA.poly[i].imag(0);
// for(int i = 0; i < base; ++i)PB.poly[i].real(B[i] * B[i]), PB.poly[i].imag(0);
for(int i = 0; i < base; ++i)PA.poly[i] = A[i] * A[i], PB.poly[i] = B[i] * B[i];
PA.FFT(DFT), PB.FFT(DFT);
for(int i = 0; i < base; ++i)P.poly[i] -= PA.poly[i] * PB.poly[i] + PA.poly[i] * PB.poly[i];
P.FFT(IDFT);
// Polynomial P[7];
// for(int i = 0; i < M; ++i)
// P[1].poly[i].real(A[i] * A[i] * A[i]), P[3].poly[i].real(A[i]), P[5].poly[i].real(A[i] * A[i]);
// for(int i = 0; i < N; ++i)
// P[2].poly[i].real(B[i]), P[4].poly[i].real(B[i] * B[i] * B[i]), P[6].poly[i].real(B[i] * B[i]);
// for(int i = 1; i <= 6; ++i)P[i].len = base, P[i].FFT(DFT);
// P[1].Print();
// P[1].FFT(DFT), P[1].FFT(IDFT);
// P[1].Print();
// P[0].len = base;
// for(int i = 0; i < base; ++i)
// for(int j = 1; j <= 5; j += 2)
// P[0].poly[i] += P[j].poly[i] * P[j + 1].poly[i];
// P[0].FFT(IDFT);
// P.Print();
basic_string < int > ans;
// for(int i = M - 1; i <= N - 1; ++i)if(fabs(P.poly[i].real()) < 1e-5)ans += i + 1 - M + 1;
for(int i = M - 1; i <= N - 1; ++i)if(P.poly[i] == 0)ans += i + 1 - M + 1;
printf("%d\n", (int)ans.size());
for(auto v : ans)printf("%d ", v);
printf("\n");
// cout << ans.size() << endl;
// for(auto v : ans)cout << v << " ";
// cout << endl;
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template < typename T >
inline T read(void){
T ret(0);
int flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
例题 #5 CF528D Fuzzy Search
题面
进行单模式串匹配,但对于一个位置的匹配可以匹配所有距离该位置距离不大于 $ k $ 的,同时字符集大小仅有 $ 4 $。
Solution
类比 P4173,对于本题我们考虑直接枚举四种字符,对于一种字符,考虑忽略掉其它所有字符,则可以认为文本串与模式串均变成 $ 01 $ 串,此时我们可以考虑对文本串中的 $ 1 $ 向左右各 $ k $ 的邻域扩散,在这之后直接做一般的单模式串匹配即可,但是注意这个东西不能用 KMP,因为我们仅需匹配模式串的 $ 1 $,模式串中的 $ 0 $ 实际上应该认为是通配符,于是仍然考虑类似 P4173 的做法,翻转模式串后,考虑列式子:
展开:
\[P(x) = \sum_{i = 0}^{x}A(i)^3 + A(i)B(x - i)^2 - 2A(i)^2B(x - i) \]这个东西自然可以通过进行两次 NTT 来做,但是我们不难发现由于 $ A(i), B(i) $ 只能为 $ 0 $ 或 $ 1 $,所以可以直接将指数的 $ 3 \rightarrow 1, 2 \rightarrow 1 $,再次化简后得到:
\[P(x) = \sum_{i = 0}^{x}A(i) + A(i)B(x - i) - 2A(i)B(x - i) \]最终得到:
\[P(x) = \sum_{i = 0}^{x}A(i) - A(i)B(x - i) \]于是做四次之后,将四次的 $ P(x) $ 加和,最终仍然为 $ 0 $ 的即会为答案贡献 $ 1 $。
Code
#define _USE_MATH_DEFINES
#include <bits/stdc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW void* Edge::operator new(size_t){static Edge* P = ed; return P++;}
#define ROPNEW_NODE void* Node::operator new(size_t){static Node* P = nd; return P++;}
using namespace std;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
#define DFT (true)
#define IDFT (false)
#define MOD (998244353ll)
template < typename T = int >
inline T read(void);
int N, M, K;
int pos[810000];
bool A[810000], B[810000], rB[810000];
int sumA[810000], sumB[810000];
int Ans[810000];
int ans(0);
ll g(3), inv_g;
string S1, S2;
ll qpow(ll a, ll b){
ll ret(1), mul(a);
while(b){
if(b & 1)ret = ret * mul % MOD;
b >>= 1;
mul = mul * mul % MOD;
}return ret;
}
class Polynomial{
private:
public:
int len;
ll poly[810000];
void Reverse(void){
for(int i = 0; i < len; ++i)
pos[i] = (pos[i >> 1] >> 1) | (i & 1 ? len >> 1 : 0);
for(int i = 0; i < len; ++i)if(i < pos[i])swap(poly[i], poly[pos[i]]);
}
void NTT(bool pat){
Reverse();
for(int siz = 2; siz <= len; siz <<= 1){
ll gn = qpow(pat ? g : inv_g, (MOD - 1) / siz);
for(auto p = poly; p != poly + len; p += siz){
int mid(siz >> 1); ll g(1);
for(int i = 0; i < mid; ++i, (g *= gn) %= MOD){
auto tmp = g * p[i + mid] % MOD;
p[i + mid] = (p[i] - tmp + MOD) % MOD;
p[i] = (p[i] + tmp) % MOD;
}
}
}
if(!pat){
ll inv_len = qpow(len, MOD - 2);
for(int i = 0; i < len; ++i)(poly[i] *= inv_len) %= MOD;
}
}
void Print(void){
printf("Polynomial(len = %d): ", len);
for(int i = 0; i < len; ++i)printf("%lld ", poly[i]);
printf("\n");
}
};
Polynomial PA, PB;
int base(1);
void Make(char flag){
for(int i = 0; i < M; ++i)A[i] = S2.at(i) == flag ? 1 : 0;
for(int i = 0; i < N; ++i)B[i] = S1.at(i) == flag ? 1 : 0;
for(int i = 0; i < base; ++i)sumA[i] = (i ? sumA[i - 1] : 0) + A[i], sumB[i] = (i ? sumB[i - 1] : 0) + B[i];
for(int i = 0; i < N; ++i)if((i + K < N ? sumB[i + K] : sumB[N - 1]) - (i - K - 1 >= 0 ? sumB[i - K - 1] : 0) > 0)rB[i] = 1; else rB[i] = 0;
// for(int i = 0; i < N; ++i)printf("sumB[%d] = %d\n", i, sumB[i]);
for(int i = 0; i < base; ++i)PA.poly[i] = A[i], PB.poly[i] = rB[i];
// PA.Print(), PB.Print();
PA.NTT(DFT), PB.NTT(DFT);
for(int i = 0; i < base; ++i)PA.poly[i] = PA.poly[i] * PB.poly[i] % MOD;
PA.NTT(IDFT);
// PA.Print();
for(int i = 0; i < base; ++i)Ans[i] += sumA[i] - PA.poly[i];
// for(int i = 0; i < base; ++i)printf("Ans[%d] = %d\n", i, Ans[i]);
}
int main(){
inv_g = qpow(g, MOD - 2);
N = read(), M = read(), K = read();
cin >> S1 >> S2;
reverse(S2.begin(), S2.end());
int clen = N + M - 1;
while(base < clen)base <<= 1;
PA.len = PB.len = base;
Make('A'), Make('T'), Make('C'), Make('G');
for(int i = M - 1; i <= N - 1; ++i)if(!Ans[i])++ans;
printf("%d\n", ans);
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template < typename T >
inline T read(void){
T ret(0);
int flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
例题 #6 P3321 [SDOI2015]序列统计
题面
存在集合 $ S $,其中仅会包含小于 $ m $ 的非负数。求从其中可重复地选出 $ n $ 个数构成排列满足所有数之积在模 $ m $ 意义下等于 $ x $ 的方案数。
Solution
令 $ h_t(i) $ 表示从集合中选取 $ 2^t $ 个数和为 $ i $ 的方案数,显然有递推:
\[h_t(x) = \sum_{i = 0}^{m - 1} h_{t - 1}(i) \times h_{t - 1}(x - i) \]显然为卷积形式,可以多项式优化,最终复杂度 $ O(m \log m \log n) $。
考虑对于取模的情况,可以将 $ [m - 1, 2m - 2] $ 之间的再覆盖加到 $ [0, m - 2] $ 的位置上即可,以此类推。
考虑如何将求和改为求积,不难发现可以通过对数函数将乘法转为加法,通过指数函数可以将加法转为乘法。于是考虑模意义下的对数函数,不难想到以原根 $ g $ 为底数,则映射关系为双射。
即令 $ \log_g{gx \bmod{m}} = x $,将原集合的所有数 $ s $ 改为 $ \log_g^s $,将 $ x $ 同理改变,这样就可以将 $ \prod s = x $ 转换为 $ \sum \log_g^s \bmod{m} = \log_g^x $,可以通过前面的 DP 解决。
同时不难发现,按照刚才的做法映射关系为映射到 $ [1, m - 1] $,这样的话处理时还要特殊处理 $ 0 $ 项,于是不难想到我们可以将 $ g^{m - 1} \bmod{m} \rightarrow 0 $ 的映射变为 $ g^0 \bmod m \rightarrow 0 $ 的映射,也就是将 $ m - 1 $ 项换到 $ 0 $ 项,这样的话答案不变但是处理时可以直接按照我们之前写的去覆盖加即可。
Tips:我这里的写法中间会有少部分的无用的复制操作,对于本题不卡常所以可以通过,对于卡常的题可能还需要注意精细实现减少多项式的无用复制操作。
Code
#define _USE_MATH_DEFINES
#include <bits/stdc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW void* Edge::operator new(size_t){static Edge* P = ed; return P++;}
#define ROPNEW_NODE void* Node::operator new(size_t){static Node* P = nd; return P++;}
using namespace std;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
#define DFT (true)
#define IDFT (false)
#define MOD (1004535809ll)
template < typename T = int >
inline T read(void);
int N, M, X, S;
int cnt[8100];
int pos[32100];
ll g(3), inv_g;
ll gm;
int toLog[8100];
ll qpow(ll a, ll b){
ll ret(1), mul(a);
while(b){
if(b & 1)ret = ret * mul % MOD;
b >>= 1;
mul = mul * mul % MOD;
}return ret;
}
class Polynomial{
private:
public:
int len;
ll poly[32100];
Polynomial(void){
len = 0;
memset(poly, 0, sizeof poly);
}
void Reverse(void){
for(int i = 0; i < len; ++i)
pos[i] = (pos[i >> 1] >> 1) | (i & 1 ? len >> 1 : 0);
for(int i = 0; i < len; ++i)if(i < pos[i])swap(poly[i], poly[pos[i]]);
}
void NTT(bool pat){
Reverse();
for(int siz = 2; siz <= len; siz <<= 1){
ll gn = qpow(pat ? g : inv_g, (MOD - 1) / siz);
for(auto p = poly; p != poly + len; p += siz){
int mid = siz >> 1; ll g(1);
for(int i = 0; i < mid; ++i, (g *= gn) %= MOD){
ll tmp = g * p[i + mid] % MOD;
p[i + mid] = (p[i] - tmp + MOD) % MOD;
p[i] = (p[i] + tmp) % MOD;
}
}
}
if(!pat){
ll inv_len = qpow(len, MOD - 2);
for(int i = 0; i < len; ++i)(poly[i] *= inv_len) %= MOD;
}
}
auto operator %= (const int mod){
for(int i = mod; i < len; ++i)poly[i] = 0;
len = min(len, mod);
}
void Print(void){
printf("Polynomial(len = %d): ", len);
for(int i = 0; i < len; ++i)printf("%lld ", poly[i]);
printf("\n");
}
};
Polynomial H[31];
Polynomial Ans;
ll GetGM(void){
for(int i = 2; true; ++i){
ll cur = i;
bool flag(true);
for(int j = 2; j <= M - 2; ++j){
(cur *= i) %= M;
if(cur == 1){flag = false; break;}
}
if(flag && cur * i % M == 1)return i;
}return -1;
}
void Mul(Polynomial *ret, Polynomial a, Polynomial b){
int base(1);
while(base < a.len + b.len - 1)base <<= 1;
a.len = b.len = base;
a.NTT(DFT), b.NTT(DFT);
for(int i = 0; i < base; ++i)a.poly[i] = a.poly[i] * b.poly[i] % MOD;
a.NTT(IDFT);
*ret %= M - 1; ret->len = M - 1;
for(int i = 0; i < M - 1; ++i)ret->poly[i] = a.poly[i];
for(int i = M - 1; i < base; ++i)(ret->poly[i % (M - 1)] += a.poly[i]) %= MOD;
}
int main(){
inv_g = qpow(g, MOD - 2);
N = read(), M = read(), X = read(), S = read();
gm = GetGM();
toLog[0] = M;
ll cur(1); toLog[cur] = 0;
for(int i = 1; i <= M - 1 - 1; ++i)(cur *= gm) %= M, toLog[cur] = i;
X = toLog[X];
for(int i = 1; i <= S; ++i)cnt[toLog[read()]]++;
for(int i = 0; i < M - 1; ++i)H[0].poly[i] = cnt[i];
H[0].len = M;
for(int i = 1; i <= 30; ++i)Mul(&H[i], H[i - 1], H[i - 1]);
Ans.len = 1, Ans.poly[0] = 1;
for(int i = 0; i <= 30; ++i)if((1 << i) & N)Mul(&Ans, Ans, H[i]);
printf("%lld\n", Ans.poly[X]);
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template < typename T >
inline T read(void){
T ret(0);
int flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
例题 #7 LG-P4491 [HAOI2018]染色
题面
对长度为 $ n $ 的序列进行染色,共有 $ m $ 种颜色,给定 $ S $,若恰好出现 $ S $ 次的颜色有 $ k $ 种则获得 $ w_k $ 的愉悦度,求对于所有染色方案的愉悦度之和。
Solution
由恰好不难想到二项式反演做法,即考虑令 $ f(i) $ 表示钦定 $ i $ 种颜色恰有 $ S $ 次的方案数,令 $ g(i) $ 表示恰有 $ i $ 种颜色恰有 $ k $ 次的方案数。
考虑意义不难想到:
\[f(i) = {m \choose i}{n \choose iS}\dfrac{(iS)!}{(S!)^i}(m - i)^{n - iS} \]同时有:
\[f(i) = \sum_{j = i}^{\min(m, \lfloor \tfrac{n}{S} \rfloor)} {j \choose i} g(j) \]此即标准二项式反演,转换为:
\[g(i) = \sum_{j = i}^{\min(m, \lfloor \tfrac{n}{S} \rfloor)} (-1)^{j - i} {j \choose i} f(j) \]由于需要求所有的 $ g(i) $,复杂度 $ O(m^2) $ 无法接受,于是尝试展开:
\[g(i) = \sum_{j = i}^{\min(m, \lfloor \tfrac{n}{S} \rfloor)} \dfrac{(-1)^{j - i} j!}{i! (j - i)!}f(j) \]转化:
\[g(i) \times i! = \sum_{j = i}^{\min(m, \lfloor \tfrac{n}{S} \rfloor)} \dfrac{(-1)^{j - i}}{(j - i)!}f(j)j! \]翻转 $ f(j)j $ 之后即满足卷积形式,NTT 优化即可,复杂度 $ O(m \log m) $。
Code
#define _USE_MATH_DEFINES
#include <bits/stdc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW void* Edge::operator new(size_t){static Edge* P = ed; return P++;}
#define ROPNEW_NODE void* Node::operator new(size_t){static Node* P = nd; return P++;}
using namespace std;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
#define DFT (true)
#define IDFT (false)
#define MOD (1004535809ll)
template < typename T = int >
inline T read(void);
int N, M, S;
int pos[410000];
ll g(3), inv_g;
ll W[410000];
ll qpow(ll a, ll b){
if(b < 0)return 0;
ll ret(1), mul(a);
while(b){
if(b & 1)ret = ret * mul % MOD;
b >>= 1;
mul = mul * mul % MOD;
}return ret;
}
class Polynomial{
private:
public:
int len;
ll poly[410000];
Polynomial(void){
len = 0;
memset(poly, 0, sizeof poly);
}
void Reverse(void){
for(int i = 0; i < len; ++i)
pos[i] = (pos[i >> 1] >> 1) | (i & 1 ? len >> 1 : 0);
for(int i = 0; i < len; ++i)if(i < pos[i])swap(poly[i], poly[pos[i]]);
}
void NTT(bool pat){
Reverse();
for(int siz = 2; siz <= len; siz <<= 1){
ll gn = qpow(pat ? g : inv_g, (MOD - 1) / siz);
for(auto p = poly; p != poly + len; p += siz){
int mid = siz >> 1; ll g(1);
for(int i = 0; i < mid; ++i, (g *= gn) %= MOD){
auto tmp = g * p[i + mid] % MOD;
p[i + mid] = (p[i] - tmp + MOD) % MOD;
p[i] = (p[i] + tmp) % MOD;
}
}
}
if(!pat){
ll inv_len = qpow(len, MOD - 2);
for(int i = 0; i < len; ++i)(poly[i] *= inv_len) %= MOD;
}
}
void Print(void){
printf("Polynomial(len = %d): ", len);
for(int i = 0; i < len; ++i)printf("%lld ", poly[i]);
printf("\n");
}
};
ll fact[11000000], inv[11000000];
void Init(void){
inv_g = qpow(g, MOD - 2);
fact[0] = 1;
for(int i = 1; i <= 10100000; ++i)fact[i] = fact[i - 1] * i % MOD;
inv[10100000] = qpow(fact[10100000], MOD - 2);
for(int i = 10099999; i >= 0; --i)inv[i] = inv[i + 1] * (i + 1) % MOD;
}
ll GetC(ll n, ll m){
if(n < m)return 0;
return fact[n] * inv[m] % MOD * inv[n - m] % MOD;
}
int main(){
Init();
N = read(), M = read(), S = read();
for(int i = 0; i <= M; ++i)W[i] = read();
Polynomial A, B;
int clen = min(M, N / S) + 1;
int base(1); while(base < clen + clen - 1)base <<= 1;
A.len = B.len = base;
for(int i = 0, mul(1); i < clen; ++i, mul *= -1)A.poly[i] = (mul * inv[i] % MOD + MOD) % MOD;
for(int i = 0; i < clen; ++i)
B.poly[i] = GetC(M, i) * GetC(N, i * S) % MOD * fact[i * S] % MOD * qpow(inv[S], i) % MOD * qpow(M - i, N - i * S) % MOD * fact[i] % MOD;
// A.Print(), B.Print();
reverse(B.poly, B.poly + clen);
// A.Print(), B.Print();
// A.NTT(DFT), A.NTT(IDFT);
// A.Print();
A.NTT(DFT), B.NTT(DFT);
for(int i = 0; i < A.len; ++i)A.poly[i] = A.poly[i] * B.poly[i] % MOD;
A.NTT(IDFT);
// A.Print();
ll ans(0);
for(int i = 0; i < clen; ++i)(ans += A.poly[clen - 1 - i] * inv[i] % MOD * W[i] % MOD) %= MOD;
printf("%lld\n", ans);
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template < typename T >
inline T read(void){
T ret(0);
int flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
例题 #8 LG-P5395 第二类斯特林数·行
题面
给定 $ n $,求 $ \forall i \in [0, n], {n \brace i} $。
Solution
直接套用 浅析排列组合、卡特兰数、斯特林数、贝尔数、二项式定理与推论及其反演、子集反演、广义容斥、范德蒙德卷积 中第二类斯特林数的通项公式,并 NTT 优化即可,复杂度 $ O(n \log n) $。
\[{n \brace i} = \sum_{j = 0}^i \dfrac{(-1)^{i - j}}{(i - j)!} \dfrac{j^n}{j!} \]Code
#define _USE_MATH_DEFINES
#include <bits/stdc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW void* Edge::operator new(size_t){static Edge* P = ed; return P++;}
#define ROPNEW_NODE void* Node::operator new(size_t){static Node* P = nd; return P++;}
using namespace std;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
#define DFT (true)
#define IDFT (false)
#define MOD (167772161ll)
template < typename T = int >
inline T read(void);
int N;
int pos[810000];
ll g(3), inv_g;
ll qpow(ll a, ll b){
if(b < 0)return 0;
ll ret(1), mul(a);
while(b){
if(b & 1)ret = ret * mul % MOD;
b >>= 1;
mul = mul * mul % MOD;
}return ret;
}
class Polynomial{
private:
public:
int len;
ll poly[810000];
Polynomial(void){
len = 0;
memset(poly, 0, sizeof poly);
}
void Reverse(void){
for(int i = 0; i < len; ++i)
pos[i] = (pos[i >> 1] >> 1) | (i & 1 ? len >> 1 : 0);
for(int i = 0; i < len; ++i)if(i < pos[i])swap(poly[i], poly[pos[i]]);
}
void NTT(bool pat){
Reverse();
for(int siz = 2; siz <= len; siz <<= 1){
ll gn = qpow(pat ? g : inv_g, (MOD - 1) / siz);
for(auto p = poly; p != poly + len; p += siz){
int mid = siz >> 1; ll g(1);
for(int i = 0; i < mid; ++i, (g *= gn) %= MOD){
auto tmp = g * p[i + mid] % MOD;
p[i + mid] = (p[i] - tmp + MOD) % MOD;
p[i] = (p[i] + tmp) % MOD;
}
}
}
if(!pat){
ll inv_len = qpow(len, MOD - 2);
for(int i = 0; i < len; ++i)(poly[i] *= inv_len) %= MOD;
}
}
void Print(void){
printf("Polynomial(len = %d): ", len);
for(int i = 0; i < len; ++i)printf("%lld ", poly[i]);
printf("\n");
}
};
ll fact[810000], inv[810000];
void Init(void){
inv_g = qpow(g, MOD - 2);
fact[0] = 1;
for(int i = 1; i <= 801000; ++i)fact[i] = fact[i - 1] * i % MOD;
inv[801000] = qpow(fact[801000], MOD - 2);
for(int i = 800999; i >= 0; --i)inv[i] = inv[i + 1] * (i + 1) % MOD;
}
int main(){
Init();
N = read();
Polynomial A, B;
for(int i = 0; i <= N; ++i)
A.poly[i] = (qpow(-1, i) * inv[i] % MOD + MOD) % MOD,
B.poly[i] = qpow(i, N) * inv[i] % MOD;
int base(1); while(base < N + 1 + N + 1 - 1)base <<= 1;
A.len = B.len = base;
A.NTT(DFT), B.NTT(DFT);
for(int i = 0; i < A.len; ++i)A.poly[i] = A.poly[i] * B.poly[i] % MOD;
A.NTT(IDFT);
for(int i = 0; i <= N; ++i)printf("%lld%c", A.poly[i], i == N ? '\n' : ' ');
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template < typename T >
inline T read(void){
T ret(0);
int flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
例题 #9 LG-P4091 [HEOI2016/TJOI2016]求和
题面
求:
\[f(n) = \sum_{i = 0}^n \sum_{j = 0}^i {i \brace j} \times 2^j \times j! \]Solution
直接推式子:
\[\begin{aligned} f(n) &= \sum_{i = 0}^n \sum_{j = 0}^i {i \brace j} \times 2^j \times j! \\ &= \sum_{i = 0}^n \sum_{j = 0}^n {i \brace j} \times 2^j \times j! \\ &= \sum_{i = 0}^n \sum_{j = 0}^n \sum_{k = 0}^j \dfrac{(-1)^{j - k}}{(j - k)!} \dfrac{k^i}{k!} \times 2^j \times j! \\ &= \sum_{j = 0}^n 2^j \times j! \sum_{k = 0}^j \dfrac{(-1)^{j - k}}{(j - k)!} \dfrac{ \sum_{i = 0}^n k^i}{k!} \\ &= \sum_{j = 0}^n 2^j \times j! \sum_{k = 0}^j \dfrac{(-1)^{j - k}}{(j - k)!} \dfrac{k^{n + 1} - 1}{(k - 1)k!} \end{aligned} \]发现满足卷积形式,可以直接 NTT 优化。
同时注意,过程中用到了等比数列求和,而等比数列求和公式在 $ q = 1 $ 时不成立。
Code
#define _USE_MATH_DEFINES
#include <bits/stdc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW void* Edge::operator new(size_t){static Edge* P = ed; return P++;}
#define ROPNEW_NODE void* Node::operator new(size_t){static Node* P = nd; return P++;}
using namespace std;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
#define DFT (true)
#define IDFT (false)
#define MOD (998244353ll)
template < typename T = int >
inline T read(void);
int N;
int pos[410000];
ll g(3), inv_g;
ll qpow(ll a, ll b){
if(b < 0)return 0;
ll ret(1), mul(a);
while(b){
if(b & 1)ret = ret * mul % MOD;
b >>= 1;
mul = mul * mul % MOD;
}return ret;
}
class Polynomial{
private:
public:
int len;
ll poly[410000];
Polynomial(void){
len = 0;
memset(poly, 0, sizeof poly);
}
void Reverse(void){
for(int i = 0; i < len; ++i)
pos[i] = (pos[i >> 1] >> 1) | (i & 1 ? len >> 1 : 0);
for(int i = 0; i < len; ++i)if(i < pos[i])swap(poly[i], poly[pos[i]]);
}
void NTT(bool pat){
Reverse();
for(int siz = 2; siz <= len; siz <<= 1){
ll gn = qpow(pat ? g : inv_g, (MOD - 1) / siz);
for(auto p = poly; p != poly + len; p += siz){
int mid = siz >> 1; ll g(1);
for(int i = 0; i < mid; ++i, (g *= gn) %= MOD){
auto tmp = g * p[i + mid] % MOD;
p[i + mid] = (p[i] - tmp + MOD) % MOD;
p[i] = (p[i] + tmp) % MOD;
}
}
}
if(!pat){
ll inv_len = qpow(len, MOD - 2);
for(int i = 0; i < len; ++i)(poly[i] *= inv_len) %= MOD;
}
}
void Print(void){
printf("Polynomial(len = %d): ", len);
for(int i = 0; i < len; ++i)printf("%lld ", poly[i]);
printf("\n");
}
};
ll fact[410000], inv[410000];
void Init(void){
inv_g = qpow(g, MOD - 2);
fact[0] = 1;
for(int i = 1; i <= 401000; ++i)fact[i] = fact[i - 1] * i % MOD;
inv[401000] = qpow(fact[401000], MOD - 2);
for(int i = 400999; i >= 0; --i)inv[i] = inv[i + 1] * (i + 1) % MOD;
}
int main(){
Init();
N = read();
Polynomial A, B;
for(int i = 0; i <= N; ++i)
A.poly[i] = (qpow(-1, i) * inv[i] % MOD + MOD) % MOD,
B.poly[i] = (qpow(i, N + 1) - 1 + MOD) % MOD * qpow((i - 1 + MOD) % MOD * fact[i] % MOD, MOD - 2) % MOD;
B.poly[1] = N + 1; //Formula does not establish when q = 1.
int base(1); while(base < N + 1 + N + 1 - 1)base <<= 1;
A.len = B.len = base;
A.NTT(DFT), B.NTT(DFT);
for(int i = 0; i < A.len; ++i)A.poly[i] = A.poly[i] * B.poly[i] % MOD;
A.NTT(IDFT);
ll ans(0);
for(int i = 0; i <= N; ++i)(ans += A.poly[i] * qpow(2, i) % MOD * fact[i] % MOD) %= MOD;
printf("%lld\n", ans);
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template < typename T >
inline T read(void){
T ret(0);
int flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
例题 #10 LG-P2791 幼儿园篮球题
题面
给定 $ L $,多组数据,给定 $ n, m ,k $,表示共有 $ n $ 个元素,其中有 $ m $ 个好的,要从中随机算出 $ k $ 个,若其中好的元素有 $ x $ 个那么贡献为 $ x^L $,求贡献的期望。对 $ 998244353 $ 取模。
Solution
显然答案式子为:
\[\dfrac{1}{n \choose k}\sum_{i = 0}^k {m \choose i}{n - m \choose k - i} i^L \]发现该式除了 $ i^L $ 复杂度都是正确的,于是考虑经典转化,用斯特林数替换 $ i^L $:
\[\begin{aligned} & \sum_{i = 0}^k {m \choose i}{n - m \choose k - i} i^L \\ =& \sum_{i = 0}^k {m \choose i}{n - m \choose k - i} \sum_{j = 0}^i {i \choose j} {L \brace j}j! \\ =& \sum_{j = 0}^k {L \brace j}j! \sum_{i = j}^k {m \choose i}{i \choose j}{n - m \choose k - i} \\ =& \sum_{j = 0}^k {L \brace j}j! {m \choose j} \sum_{i = j}^k {m - j \choose i - j}{n - m \choose k - i} \\ =& \sum_{j = 0}^k {L \brace j}j! {m \choose j} \sum_{i = 0}^{k - j} {m - j \choose i}{n - m \choose k - i - j} \\ =& \sum_{j = 0}^k {L \brace j}j! {m \choose j} {n - j \choose k - j} \end{aligned} \]于是此时发现可以快速处理,$ O(L \log L) $ 预处理同行斯特林数,然后枚举 $ j $ 即可,复杂度 $ O(L \log L + SL) $。
然后发现被卡常了,我直接三倍常数,尝试把组合数带进去化简一下:
\[\begin{aligned} & \dfrac{1}{n \choose k}\sum_{j = 0}^k {L \brace j}j! {m \choose j} {n - j \choose k - j} \\ =& \sum_{j = 0}^k {L \brace j}j! \dfrac{m!}{j!(m - j!)}\dfrac{(n - j)!}{(k - j)!(n - k)!}\dfrac{k! (n - k)!}{n!} \\ =& \sum_{j = 0}^k {L \brace j} \dfrac{m!}{(m - j!)}\dfrac{(n - j)!}{(k - j)!}\dfrac{k!}{n!} \end{aligned} \]然后发现此题完全不卡常,是我写的问题,最开始的写法最后计算答案真正枚举到 $ k $ 了,而后面的显然均为 $ 0 $,所以直接计算:
\[\dfrac{1}{n \choose k}\sum_{j = 0}^L {L \brace j}j! {m \choose j} {n - j \choose k - j} \]就可以稳稳通过了,同时注意如果要采用后者的优化后的式子,需要处理好组合数 $ n \lt 0 \lor m \lt 0 $ 时方案数为 $ 0 $,当然前者也需要处理。
Code
#define _USE_MATH_DEFINES
#include <bits/stdc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW void* Edge::operator new(size_t){static Edge* P = ed; return P++;}
#define ROPNEW_NODE void* Node::operator new(size_t){static Node* P = nd; return P++;}
using namespace std;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
#define DFT (true)
#define IDFT (false)
#define MOD (998244353ll)
template < typename T = int >
inline T read(void);
int S, L, N, M, K;
int pos[810000];
ll g(3), inv_g;
ll qpow(ll a, ll b){
if(b < 0)return 0;
ll ret(1), mul(a);
while(b){
if(b & 1)ret = ret * mul % MOD;
b >>= 1;
mul = mul * mul % MOD;
}return ret;
}
class Polynomial{
private:
public:
int len;
ll poly[810000];
Polynomial(void){
len = 0;
memset(poly, 0, sizeof poly);
}
void Reverse(void){
for(int i = 0; i < len; ++i)
pos[i] = (pos[i >> 1] >> 1) | (i & 1 ? len >> 1 : 0);
for(int i = 0; i < len; ++i)if(i < pos[i])swap(poly[i], poly[pos[i]]);
}
void NTT(bool pat){
Reverse();
for(int siz = 2; siz <= len; siz <<= 1){
ll gn = qpow(pat ? g : inv_g, (MOD - 1) / siz);
for(auto p = poly; p != poly + len; p += siz){
int mid = siz >> 1; ll g(1);
for(int i = 0; i < mid; ++i, (g *= gn) %= MOD){
auto tmp = g * p[i + mid] % MOD;
p[i + mid] = (p[i] - tmp + MOD) % MOD;
p[i] = (p[i] + tmp) % MOD;
}
}
}
if(!pat){
ll inv_len = qpow(len, MOD - 2);
for(int i = 0; i < len; ++i)(poly[i] *= inv_len) %= MOD;
}
}
void Print(void){
printf("Polynomial(len = %d): ", len);
for(int i = 0; i < len; ++i)printf("%lld ", poly[i]);
printf("\n");
}
};
int fact[21000000], inv[21000000];
void Init(void){
inv_g = qpow(g, MOD - 2);
fact[0] = 1;
for(int i = 1; i <= 20100000; ++i)fact[i] = (ll)fact[i - 1] * i % MOD;
inv[20100000] = qpow(fact[20100000], MOD - 2);
for(int i = 20099999; i >= 0; --i)inv[i] = (ll)inv[i + 1] * (i + 1) % MOD;
}
ll GetC(ll n, ll m){
if(n < m || n < 0 || m < 0)return 0;
return (ll)fact[n] * inv[m] % MOD * inv[n - m] % MOD;
}
int main(){
Init();
(void)read(), (void)read(), S = read(), L = read();
Polynomial A, B;
for(int i = 0; i <= L; ++i)
A.poly[i] = (qpow(-1, i) * inv[i] % MOD + MOD) % MOD,
B.poly[i] = qpow(i, L) * inv[i] % MOD;
int base(1); while(base < L + 1 + L + 1 - 1)base <<= 1;
A.len = B.len = base;
A.NTT(DFT), B.NTT(DFT);
for(int i = 0; i < A.len; ++i)A.poly[i] = A.poly[i] * B.poly[i] % MOD;
A.NTT(IDFT);
while(S--){
N = read(), M = read(), K = read();
ll ans(0);
for(int i = 0; i <= L; ++i)
(ans += A.poly[i] * fact[i] % MOD * GetC(M, i) % MOD * GetC(N - i, K - i) % MOD) %= MOD;
printf("%lld\n", ans * inv[N] % MOD * fact[K] % MOD * fact[N - K] % MOD);
}
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template < typename T >
inline T read(void){
T ret(0);
int flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
多项式取模
这个没什么可说的,是个概念性问题,可以认为如对于 $ A(x) \bmod{x^n} $,即表示保留多项式 $ A(x) $ 的 $ [0, n - 1] $ 次方项,也就是保留前 $ n $ 项。
多项式求逆
显然是在模意义下的,简而言之就是给定 $ F(x) $,求 $ G(x) $ 满足 $ F(x) \ast G(x) \equiv 1 \pmod{x^n} $。
模板题:P4238 【模板】多项式乘法逆。
尝试将问题规模缩减。
考虑如果我们已知存在 $ H(x) $ 满足 $ F(x) \ast H(x) \equiv 1 \pmod{x^{\lceil \tfrac{n}{2} \rceil}} $。
又显然有 $ F(x) \ast G(x) \equiv 1 \pmod{x^{\lceil \tfrac{n}{2} \rceil}} $。
两式相减得 $ F(x) \ast (G(x) - H(x)) \equiv 0 \pmod{x^{\lceil \tfrac{n}{2} \rceil}} $。
显然 $ F(x) $ 已给定,则有 $ G(x) - H(x) \equiv 0 \pmod{x^{\lceil \tfrac{n}{2} \rceil}} $。
同余式两侧分别平方,令 $ P(x) = (G(x) - H(x))^2 $,则有 $ P_i = \sum_{j = 0}^{i} (G(x) - H(x))j(G(x) - H(x)) $,显然 $ j $ 和 $ i - j $ 中至少有一个不大于 $ \lceil \dfrac{n}{2} \rceil $,所以一定有 $ P(x) \equiv 0 \pmod{x^n} $。
展开即为:$ G(x)^2 + H(x)^2 - 2G(x)H(x) \equiv 0 \pmod{x^{n}} $。
同余式两边各乘一个 $ F(x) $ 则有:$ G(x) \equiv 2H(x) - F(x)H(x)^2 \pmod{x^n} $。
此时可以发现我们将问题规模缩小了一半,则可以如此递归下去。
显然边界为 $ n = 1 $ 的时候,多项式求逆退化成一般的乘法逆元,直接求即可。
通过主定理分析复杂度,不难发现合并可以通过 NTT 优化到 $ O(n \log n) \(,则有:\) T(n) = T(\dfrac{n}{2}) + O(n \log n) $。
故最终复杂度应为 $ O(n \log n) $。
然后这个代码实现比较乱,因为空间卡的比较严格,然后我最开始想封装一下,但是递归导致空间爆炸,并且实现上在 DFT 之后可以直接合并而不需要这么多操作,不过懒得改了,最后卡过去了,下次一定。
Code
#define _USE_MATH_DEFINES
#include <bits/stdc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
using namespace std;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
#define MOD (998244353ll)
#define DFT (true)
#define IDFT (false)
template < typename T = int >
inline T read(void);
int N;
int lim;
ll g = 3, inv_g;
int pos[280000];
ll qpow(ll a, ll b){
ll ret(1), mul(a);
while(b){
if(b & 1)ret = ret * mul % MOD;
b >>= 1;
mul = mul * mul % MOD;
}return ret;
}
class Polynomial{
private:
public:
int len;
int P[280000];
void Reverse(void){
pos[0] = 0;
for(int i = 1; i <= len - 1; ++i){
pos[i] = pos[i >> 1] >> 1;
if(i & 1)pos[i] |= len >> 1;
}for(int i = 0; i <= len - 1; ++i)if(i < pos[i])swap(P[i], P[pos[i]]);
}
void NTT(bool pat){
Reverse();
for(int siz = 2; siz <= len; siz <<= 1){
ll gn = qpow(pat ? g : inv_g, (MOD - 1) / siz);
for(int* p = P; p != P + len; p += siz){
int mid = siz >> 1; ll g(1);
for(int i = 0; i < mid; ++i, (g *= gn) %= MOD){
ll tmp = (ll)g * p[i + mid] % MOD;
p[i + mid] = ((ll)p[i] - tmp) % MOD;
p[i] = ((ll)p[i] + tmp) % MOD;
}
}
}
if(!pat){
ll inv_len = qpow(len, MOD - 2);
for(int i = 0; i <= len - 1; ++i)P[i] = ((ll)P[i] * inv_len) % MOD;
}
}
void Print(void){
for(int i = 0; i <= len - 1; ++i)printf("%d%c", P[i], i == len - 1 ? '\n' : ' ');
}
Polynomial operator %= (const ll &mod){
for(int i = mod; i <= len - 1; ++i)P[i] = 0;
len = mod;
return *this;
}
Polynomial operator *= (Polynomial B){
int rlen(1);
while(rlen < len + B.len)rlen <<= 1;
len = B.len = rlen;
// printf("len = %d\n", rlen);
// ret.len = rlen;
// A.Print(), B.Print();
NTT(DFT), B.NTT(DFT);
// A.Print(), B.Print();
for(int i = 0; i <= len - 1; ++i)P[i] = (ll)P[i] * B.P[i] % MOD;
NTT(IDFT);
// ret.Print();
return (*this) %= lim;
}
Polynomial operator *= (const ll &mul){
for(int i = 0; i <= len - 1; ++i)P[i] = ((ll)P[i] * mul) % MOD;
return *this;
}
Polynomial operator -= (const Polynomial &B){
len = max(len, B.len);
for(int i = 0; i <= len - 1; ++i)P[i] = (((ll)P[i] - (ll)B.P[i]) % MOD + MOD) % MOD;
return *this;
}
}F, H, tmp;
Polynomial Make(int len = N){
// printf("making len = %d\n", len);
if(len == 1){
Polynomial ret;
ret.len = 1, ret.P[0] = qpow(F.P[0], MOD - 2);
return ret;
}
H = Make(int(ceil((double)len / 2.0)));
// H.Print();
lim = len;
// printf("len = %d, 2H:", len); (H * 2).Print();
// printf("F: "); F.Print();
// printf("F * H: "); (F * H).Print();
// printf("F * H * H: "); (F * H * H).Print();
tmp = H;
return (H *= 2) -= ((tmp *= H) *= F);
// return H * 2 - F * H * H;
}
int main(){
// freopen("P4238_16.in", "r", stdin);
inv_g = qpow(g, MOD - 2);
F.len = N = read();
for(int i = 0; i <= N - 1; ++i)F.P[i] = read();
// decltype(F) tmp; tmp.len = 1; tmp.P[0] = 1;
// F.Print();
// tmp.Print();
// (F * tmp).Print();
Make().Print();
// for(int i = 0; i <= N - 1; ++i)printf("%lld%c", G.P[i], i == N - 1 ? '\n' : ' ');
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template < typename T >
inline T read(void){
T ret(0);
int flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
例题 #2 LG-P4841 [集训队作业2013]城市规划
题面
求 $ n $ 个点的简单有标号无向连通图数量。
Solution
令 $ f(x) $ 为 $ x $ 个点的无向连通图数量,$ g(x) $ 为 $ x $ 个点的无向图数量,首先显然有 $ g(n) = 2^{n \choose 2} $,同时我们考虑类似 FZT 的思想,枚举 $ 1 $ 节点所在连通块的大小,即:
\[g(n) = \sum_{i = 1}^{n} {n - 1 \choose i - 1}f(i)g(n - i) \]则有:
\[\sum_{i = 1}^{n} {n - 1 \choose i - 1}f(i)g(n - i) = 2^{n \choose 2} \]继续推式子:
\[\sum_{i = 1}^n \dfrac{(n - 1)!}{(i - 1)!(n - i)!}f(i)g(n - i) = 2^{n \choose 2} \]整理一下:
\[\dfrac{2^{n \choose 2}}{(n - 1)!} = \sum_{i = 1}^n \dfrac{f(i)}{(i - 1)!} \dfrac{2^{n - i \choose 2}}{(n - i)!} \]考虑进行如下定义:
\[F(x) = \sum_{i = 1}^{+\infty}\dfrac{f(i)}{(i - 1)!}x^i \]\[G(x) = \sum_{i = 1}^{+\infty}\dfrac{2^{i \choose 2}}{i!}x^i \]\[H(x) = \sum_{i = 1}^{+\infty} \dfrac{2^{i \choose 2}}{(i - 1)!}x^i \]则有:
\[H = F \ast G \pmod{x^{n + 1}} \]转化后答案即为:
\[F = H \ast G^{-1} \pmod{x^{n + 1}} \]使用多项式求逆即可解决。
Code
#define _USE_MATH_DEFINES
#include <bits/stdc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW void* Edge::operator new(size_t){static Edge* P = ed; return P++;}
#define ROPNEW_NODE void* Node::operator new(size_t){static Node* P = nd; return P++;}
using namespace std;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
#define DFT (true)
#define IDFT (false)
#define MOD (1004535809ll)
template < typename T = int >
inline T read(void);
int N;
ll g = 3, inv_g;
int pos[300000];
ll qpow(ll a, ll b){
ll ret(1), mul(a);
while(b){
if(b & 1)ret = ret * mul % MOD;
b >>= 1;
mul = mul * mul % MOD;
}return ret;
}
class Polynomial{
private:
public:
int len;
ll poly[300000];
Polynomial(void){
len = 0;
memset(poly, 0, sizeof poly);
}
void Reverse(void){
memset(pos, 0, sizeof(int) * (len + 10));
// memset(pos, 0, sizeof pos);
for(int i = 0; i < len; ++i)
pos[i] = (pos[i >> 1] >> 1) | (i & 1 ? len >> 1 : 0);
for(int i = 0; i < len; ++i)if(i < pos[i])swap(poly[i], poly[pos[i]]);
}
void NTT(bool pat){
Reverse();
for(int siz = 2; siz <= len; siz <<= 1){
ll gn = qpow(pat ? g : inv_g, (MOD - 1) / siz);
for(auto p = poly; p != poly + len; p += siz){
int mid = siz >> 1; ll g(1);
for(int i = 0; i < mid; ++i, (g *= gn) %= MOD){
auto tmp = g * p[i + mid] % MOD;
p[i + mid] = (p[i] - tmp + MOD) % MOD;
p[i] = (p[i] + tmp) % MOD;
}
}
}
if(!pat){
ll inv_len = qpow(len, MOD - 2);
for(int i = 0; i < len; ++i)(poly[i] *= inv_len) %= MOD;
}
}
auto operator %= (const int &mod){
for(int i = mod; i <= len; ++i)poly[i] = 0;
len = min(len, mod);
}
void Print(void){
printf("Polynomial(len = %d): ", len);
for(int i = 0; i < len; ++i)printf("%lld ", poly[i]);
printf("\n");
}
};
Polynomial F, H;
Polynomial CalInv(Polynomial &baseF, int len){
// static Polynomial F;
// Polynomial H;
if(len == 1){
// Polynomial ret;
H.len = 1, H.poly[0] = qpow(baseF.poly[0], MOD - 2);
return H;
}
H = CalInv(baseF, (len + 1) >> 1);
F = baseF;
int clen = H.len + H.len + F.len - 2;
int base(1); while(base < clen)base <<= 1;
H.len = F.len = base;
H.NTT(DFT), F.NTT(DFT);
for(int i = 0; i < H.len; ++i)H.poly[i] = (2 * H.poly[i] % MOD - F.poly[i] * H.poly[i] % MOD * H.poly[i] % MOD + MOD) % MOD;
H.NTT(IDFT), F.NTT(IDFT);
H %= len, F %= len;
return H;
}
ll fact[310000], inv[310000];
void Init(void){
inv_g = qpow(g, MOD - 2);
fact[0] = 1;
for(int i = 1; i <= 300000; ++i)fact[i] = fact[i - 1] * i % MOD;
inv[300000] = qpow(fact[300000], MOD - 2);
for(int i = 299999; i >= 0; --i)inv[i] = inv[i + 1] * (i + 1) % MOD;
}
ll GetC2(ll n){
if(n < 2)return 0;
return n * (n - 1) / 2;
}
int main(){
Init();
N = read();
Polynomial G, H;
G.len = H.len = N + 1;
for(int i = 0; i < G.len; ++i)G.poly[i] = qpow(2, GetC2(i) % (MOD - 1)) * inv[i] % MOD;
for(int i = 1; i < H.len; ++i)H.poly[i] = qpow(2, GetC2(i) % (MOD - 1)) * inv[i - 1] % MOD;
// G.Print(), H.Print();
G = CalInv(G, G.len);
// G.Print();
int clen = G.len + H.len - 1;
int base(1); while(base < clen)base <<= 1;
G.len = H.len = base;
G.NTT(DFT), H.NTT(DFT);
for(int i = 0; i < H.len; ++i)H.poly[i] = H.poly[i] * G.poly[i] % MOD;
H.NTT(IDFT);
printf("%lld\n", H.poly[N] * fact[N - 1] % MOD);
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template < typename T >
inline T read(void){
T ret(0);
int flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
UPD
update-2022_12_22 初稿
update-2023_01_31 修复了多项式求逆复杂度分析的错误
update-2023_01_31 添加例题 #1 #2 #3
update-2023_02_01 添加例题 #4 #5 #6
update-2023_02_06 添加例题 #8 #9 #10
标签:ll,int,多项式,void,len,ret,浅析,MOD From: https://www.cnblogs.com/tsawke/p/17124394.html