是一道dp好题。
对于一个划分,逆序对乘积的期望,即为每个划分每条线段中选两个数,所有这些数对都是逆序对的概率求和。
同时我们注意到,我们可以将偶数位置排序的限制,改成偶数位置也可以任选,但是只有顺序正确的方案是合法的,最后乘 \(n!\) 即可。
这道题最妙的地方是通过树来统计概率。
一棵树给顶点随机一个排列,每个点标号均比父亲小的概率,为所有节点子树大小倒数的乘积。利用这个东西来为偏序关系计数。
考虑所有偶数位置,显然是递增的。所有可以先建出来一条链。
考虑对每段选的位置分类讨论。
- 选两个奇数位置,概率为 \(\frac{1}{2}\)
- 选两个偶数位置,概率为 \(0\).
- 一奇一偶,偶数位置在奇数前面,就相当于在树上添加一个节点连向偶数位置所对应的点。
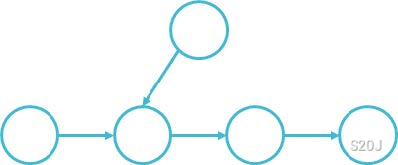
- 一偶一奇,奇数位置在偶数前面,如果连边的话就不是一棵树了,所有考虑容斥,用 \(1\) 减去不是逆序对的概率。
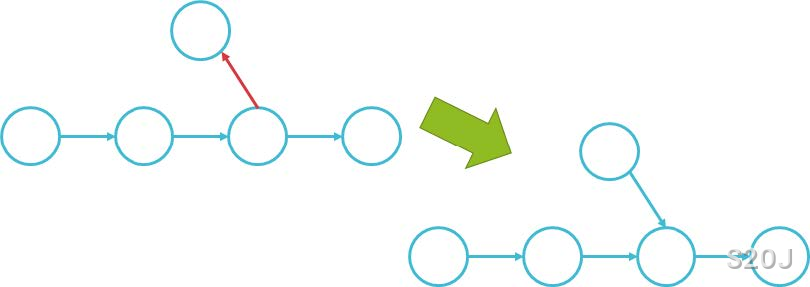
设集合 \(S\) 表示被奇数节点连向的偶数节点集合,那么贡献要乘上 \(\frac{1}{(n+|S|)!}\prod_{i=1}^{|S|}(s_i+i - 1)\)
具体dp见 【题解】#1140. 排列(permutation) - 博客 - lihaosen的博客 (sjzezoj.com)
标签:排列,奇数,位置,偶数,概率,permutation,节点,逆序 From: https://www.cnblogs.com/i209M/p/17120901.html