IOI 2022 D1T1 Fish
题目大意:
有一个 \(N\times N\) 的网格,其中的 \(M\) 个位置有垒球,第 \(i\) 个垒球的位置为 \((x_i,y_i)\),重量为 \(w_i\)。
你可以为每一列 \(c\) 选择一个前缀的行 \(1,2,\ldots,\ldots,r_c\) 修建长堤,这样 \((1,c),(2,c),\ldots,(r_c,c)\) 这些位置就会被长堤覆盖。
如果一个垒球的位置没有被长堤覆盖,且其左右相邻的位置至少有一个被长堤覆盖,那么就会有一个 ix35 走到长堤上捡起这个垒球,即如果垒球的位置为 \((x,y)\),它能被捡起当且仅当 \((x,y)\) 未被长堤覆盖且 \((x,y-1),(x,y+1)\) 至少有一个被长堤覆盖。
求最多能捡起总重多少的垒球。
\(N\leq 10^5,\ M\leq 3\times 10^5\)
题解:
假设 \(r_{c-1}<r_c>r_{c+1}\),那么第 \(c\) 列的垒球都不能被捡起,所以不如直接把第 \(c\) 列修到顶,即 \(r_c\) 可以改为 \(N\)。
假设 \(r_{c-1}>r_c<r_{c+1}\),那么第 \(c\) 列不如不修,所以 \(r_c\) 可以改为 \(0\)。
于是我们观察长堤的形状,发现修建了长堤的列可以分成若干连续段,每一段内 \(r_c\) 先递增后递减。
据此容易写出 DP,时间复杂度为 \(O(M\log M+N)\)。
IOI 2022 D1T2 Prison
题目大意:
有 \(500\) 个囚犯,还有一个房间,房间中有两个袋子 \(A,B\),分别装有 \(n_A,n_B\) 个垒球,此外还有一个数字 \(x\),初始为 \(0\)。囚犯们已知 \(1\leq n_A,n_B\leq N\) 且 \(n_A\ne n_B\),他们的目标是指出 \(n_A\) 和 \(n_B\) 的大小关系。
现在会按照随机的顺序每次叫一个囚犯进房间,此时囚犯可以看到数字 \(x\),并做出两种选择之一:打开袋子 \(A\),或者打开袋子 \(B\),即获知 \(n_A\) 或 \(n_B\)。
此时囚犯知道了 \(x\) 以及一个袋子中的垒球数量,他可以做出三种选择之一:指出 \(n_A<n_B\),或者指出 \(n_B<n_A\),或者将 \(x\) 修改为 \(x'\)(也可以 \(x'=x\))。
你需要构造一种策略,使得任意时刻 \(0\leq x\leq X\),且在 \(500\) 个囚犯都进去过一次之前得到 \(n_A,n_B\) 的大小关系。
\(N\leq 5000\),当你构造的 \(X\) 满足 \(X\leq 20\) 时得满分。
题解:
这里写的就是我的思考过程。
首先考虑一个最最 naive 的方法:考虑 \(n_A,n_B\) 的二进制表示,前两个人比较 \(n_A,n_B\) 的最高位,第三个和第四个人比较 \(n_A,n_B\) 的次高位,以此类推,那么可以实现如下:
- 第 \(2i\) 个人离开房间后确保 \(x\) 为 \(3i\);
- 第 \(2i+1\) 个人来到房间,会发现 \(x\) 为 \(3i\),于是查看 \(n_A\),如果 \(n_A\) 第 \(i\) 高位为 \(0\) 则将 \(x\) 改为 \(3i+1\),否则改为 \(3i+2\);
- 第 \(2i+2\) 个人来到房间,根据 \(x\) 是 \(3i+1\) 还是 \(3i+2\) 就可以知道 \(n_A\) 第 \(i\) 高位是 \(0\) 还是 \(1\),他再查看 \(n_B\),如果这一位不同,那么可以直接得到答案,否则就把 \(x\) 改成 \(3i+3\),再比较下一位。
这样需要 \(X=38\) 左右。
我们将这方法略作修改,如果第 \(2\) 个人进来看到 \(n_A,n_B\) 最高位相同,并不是只能把 \(x\) 改成 \(3\) 然后交给下一个人,实际上他还掌握更多信息,比如 \(n_B\) 的次高位,于是我们将策略改成如下:
- 第 \(1\) 个人来到房间,会发现 \(x=0\),查看 \(n_A\),根据最高位跳到 \(x=1\) 或 \(x=2\);
- 第 \(2i\) 个人来到房间,根据 \(x\) 的奇偶性知道 \(n_A\) 当前比较位是 \(0\) 还是 \(1\),然后查看 \(n_B\),如果不同则直接返回,否则看 \(n_B\) 的下一位,根据 \(0\) 还是 \(1\) 跳到两个不同的 \(x\);
- 第 \(2i+1\) 个人同理,不过查看的是 \(n_A\)。
这样只需要 \(2\log N\) 次,即 \(X=26\)。
再优化一下,发现这里采用二进制不如采用三进制,\(3^8>N\),所以只需要 \(X=3\times 8=24\) 即可。
再想一想,其实对于不同的数据范围可以采用不同的进制,于是我们考虑 DP,令 \(f(i)\) 表示 \(N=i\) 需要的最小的 \(X\),枚举将 \(i\) 分成 \(j\) 段,那么 \(f(i)\leftarrow f(\lceil\dfrac{i}{j}\rceil)+j\),这样应该可以 \(X=22\) 或者 \(X=21\)。
现在只需要卡一下常数就可以了,我们注意到如果第一个人进去发现 \(n_A=1\) 或者 \(n_A=N\) 都可以直接返回结果(因为保证 \(n_A\ne n_B\)),所以我们每次可以把边上两个数砍掉,于是转移变成 \(f(i)\leftarrow f(\lceil\dfrac{i-2}{j}\rceil)+j\),这样就能顺利得到 \(X=20\) 的解。
IOI 2022 D1T3 Towers
题目大意:
有 \(N\) 座塔,第 \(i\) 座塔高度为 \(h_i\),保证高度两两不同。
现在有 \(Q\) 个询问,每个询问给定 \(l,r,d\),询问从 \([l,r]\) 中至多可以选择多少个塔,使得他们两两可以 \(d\)-通信。
两座塔 \(i<j\) 可以 \(d\)-通信,当且仅当存在一座塔 \(k\) 使得 \(i<k<j\) 且 \(h_k-d\ge\max(h_i,h_j)\)。
垒球。
\(N,Q\leq 10^5\)。
题解:
对于一个确定的 \(d\),令 \(l_i\) 表示 \(i\) 左边第一个比 \(i\) 高了至少 \(d\) 的位置,\(r_i\) 表示 \(i\) 右边第一个比 \(i\) 高了至少 \(d\) 的位置。
那么两座塔 \(i<j\) 能 \(d\)-通信,当且仅当 \(r_i\leq l_j\),即它们对应的区间 \([l_i,r_i)\) 无交。
同时易证以下两个结论:
- 如果 \(i<j\) 满足 \(l_j<r_i\),那么一定有 \(l_j\leq l_i\),即不可能两个区间既不为包含关系,又相交。
- 如果对于某个 \(d\) 有 \([l_i,r_i)\subseteq [l_j,r_j)\),那么对于更大的 \(d\),这一关系也成立。
于是我们可以从小到大扫描 \(d\),维护当前没有包含任何其他 \([l_j,r_j)\) 的区间 \([l_i,r_i)\),根据第一个结论,它们是两两无交的。我们称这些区间为 \(d\) 对应的有效区间。
扫描过程中维护的方法是:用一个链表记录当前的有效区间,并且用优先队列记录每个区间在什么时间(即 \(d\) 增大到多少时)会和左边或右边合并,然后在合并时删去一个元素即可。由于询问在线,所以需要用主席树记录每个时刻的有效区间。
询问 \((L,R,d)\) 时,我们首先找到这个 \(d\) 对应的情况下,\([L,R]\) 中有多少个有效区间(一个有效区间 \([l_i,r_i)\) 在 \([L,R]\) 中定义为其中心点 \(i\) 在 \([L,R]\) 中)。
那么这些有效区间的中心一定是要选择的了,但是可能还不全面,因为左右两边可能还需要各补选 \(0\) 个或 \(1\) 个塔(这是因为可能某个有效区间与 \([L,R]\) 有交,但是其中心不在 \([L,R]\) 中,就没统计到)。
这个稍微讨论一下即可:
- 如果 \([L,R]\) 中一个有效区间都没有,那么我们找到 \([L,R]\) 中高度的最大值 \(h_m\),显然最多只能在 \(m\) 左右各选一个,判断一下行不行即可;
- 如果 \([L,R]\) 中有至少一个有效区间,那么我们找到第一个有效区间左侧的最大值 \(h_m\),考虑能不能在 \(h_m\) 左边多选一个即可(即 \([L,m-1]\) 的最小值是否不超过 \(h_m-d\)),右边同理。
用 ST 表预处理区间最值。
时间复杂度为 \(O((N+Q)\log N)\)。
IOI 2022 D2T1 Circuit
题目大意:
给定一个 \(N\) 个非叶结点,\(M\) 个叶结点的值,叶结点有初值 \(0\) 或 \(1\),某个非叶结点如果有 \(x\) 个儿子,则需要设置一个参数 \(y\in [1,x]\),表示如果其儿子有至少 \(y\) 个的值为 \(1\),那么它的值也为 \(1\)。
现在进行 \(Q\) 次操作,每次翻转编号在区间 \([l,r]\) 内的叶结点的初值(\(0\) 变成 \(1\),\(1\) 变成 \(0\)),然后询问有多少种为非叶结点设置参数的方案,使得根结点值为 \(1\),对 \(10^9+2022\) 取模。
\(N,M,Q\leq 10^5\)
题解:
如果你是赛后做题,那么解题的关键或许是看到排行榜——有一车人过了这题,说明这题是水题。
或者是觉得这题看上去非常不可做,因为编号区间和树的形态并无关联,我们不可能用任何树上的数据解构解决此题。
无论如何,我们可以猜想:每个非叶结点对答案的贡献独立,幸运的是这是对的,证明并不困难,略。
于是首先树形 DP 算出每个非叶结点单独为黑色时的答案,然后用线段树维护总的答案即可,时间复杂度为 \(O(Q\log M+N+M)\)。
IOI 2022 D2T2 Insects
题目大意:
现在有 \(N\) 个未知数 \(a_{1\ldots n}\),还有一台神秘机器,机器初始是空的,你可以进行下列三种操作:
- 将一个数 \(a_i\) 加入机器;
- 将一个数 \(a_i\) 取出机器;
- 询问机器里出现次数最多的数的出现次数。
你需要求出 \(a_{1\ldots n}\) 中出现次数最少的数的出现次数,设每种操作进行次数的最大值为 \(Q\)。
\(N\leq 2000\),\(Q\leq 3N\) 可得满分。
题解:
首先可以想到一个 \(O(N^2)\) 次操作的算法:每次放一对数进去,就能知道它们是否相等。
还有一种 \(O(N^2)\) 次操作的算法(记为青蛙算法):每次选择一个数,然后得到与它相等的所有数(加入一个别的数如果众数出现次数没有增加则说明不相等)。
还有一种 \(O(N^2)\) 次操作的算法(记为垒球算法):每次选择当前剩下的所有不同的数各一个(时刻保持众数出现次数为 \(1\) 即可),这样当某一次得到的不同的数的个数和上一次不同时,就知道出现次数最少的已经取完了。
综合青蛙算法和垒球算法,可以得到 \(O(N\sqrt N)\) 的算法。
考虑垒球算法的扩展:如果保持众数出现次数始终小于等于 \(C\),就可以得到每个数的前 \(C\) 次出现,设不同的数有 \(x\) 种,如果选出了恰好 \(Cx\) 个数则说明出现次数最少的数也出现了 \(\ge C\) 次,否则说明是 \(<C\) 次。
所以可以二分,得到了 \(O(N\log N)\) 的垒球算法。
然后发现这个二分的操作次数实际上可以变成 \(O(N)\),因为如果二分之后发现答案 \(\ge C\),那么此时已经放进机器里的就不用动了,可以看成总数大致减半;如果二分之后答案 \(<C\),那么此刻不在机器里的数就可以全部扔掉了,总数也大致减半,根据等比数列求和这就是 \(3N\) 次左右的。
然后一交获得了 \(99\) 分的好成绩,下面使用你的独门技巧乱搞卡常即可。这里我的方法是在判断时只要某个时刻机器里已经有 \(Cx\) 个数就直接退出循环,没必要加剩下的数,同时为了防卡,初始序列要随机重排。
IOI 2022 D2T3 Islands
题目大意:
有一张 \(N\) 个点,\(M\) 条边的有向图,你需要从点 \(1\) 出发走一些边回到点 \(1\),要求:
- 一条边经过后就会反向,也就是下次经过必须是从反方向经过;
- 不能连续经过同一条边。
构造一组方案,或说明无解。
\(N\leq 10^5,\ M\leq 2\times 10^5\)
题解:
如果一个结点出度为 \(0\),那么走到这里就寄了,所以可以删掉。
删掉之后可能会导致另一些点出度也变为 \(0\),也要删掉,这个可以做一次拓扑排序,就相当于我们删掉了所有不能走到环的点。
现在我们断言,如果点 \(1\) 的出度 \(\ge 2\),那么一定有解,下面给出构造。
事实上考虑下列结构:由于不存在零出度点,所以我们可以为每个点(除了 \(1\))指定一条出边,这样整张图就形成了若干个基环树,以及一棵以 \(1\) 为根的树,如下图所示:
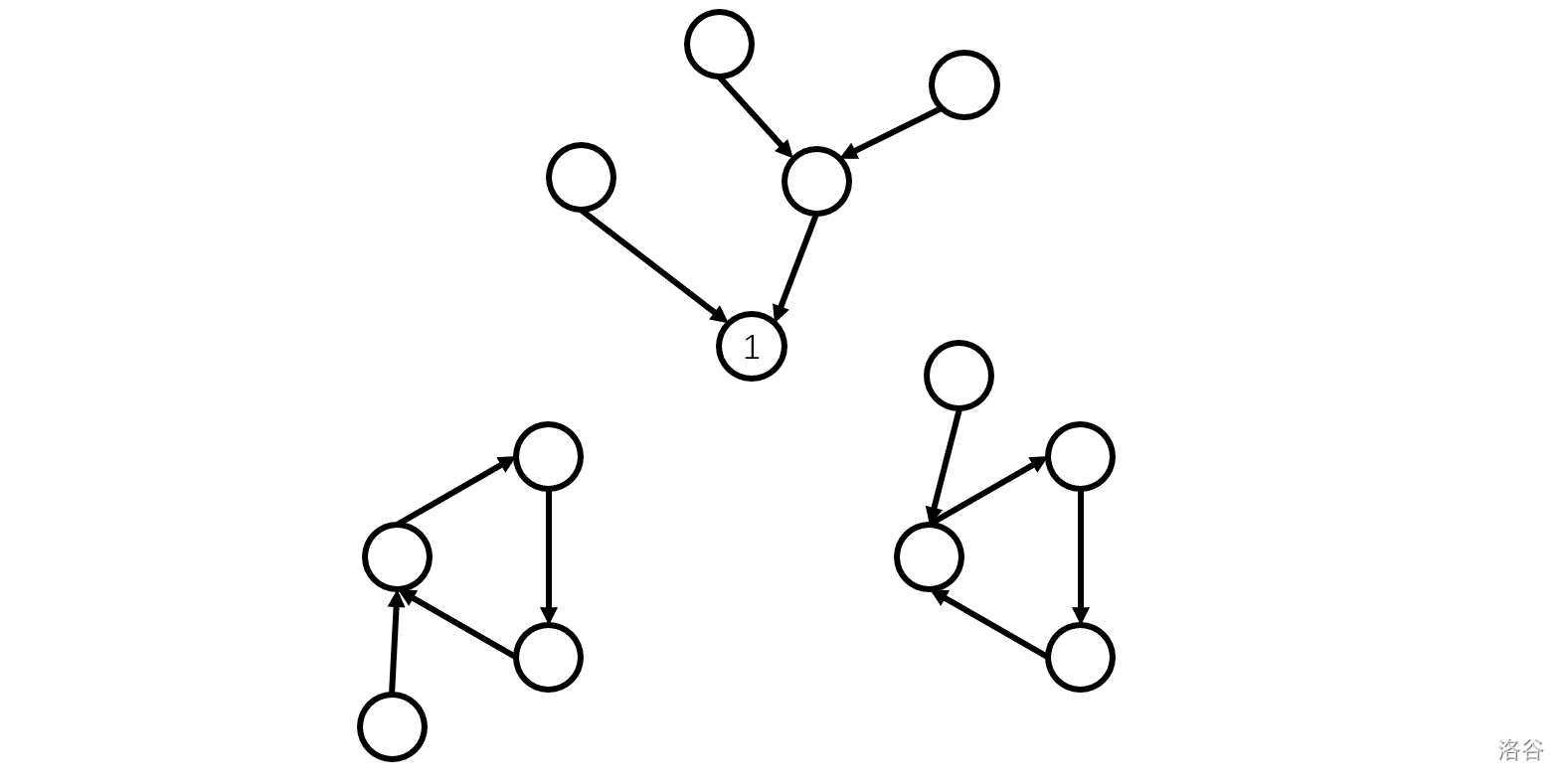
现在我们加上 \(1\) 的两条出边,那么有以下两种情况:
-
Case 1:至少一条出边指向以 \(1\) 为根的树外。
如下图所示,\(y,z\) 是出边到达的点,至少有一个在某个基环树上。
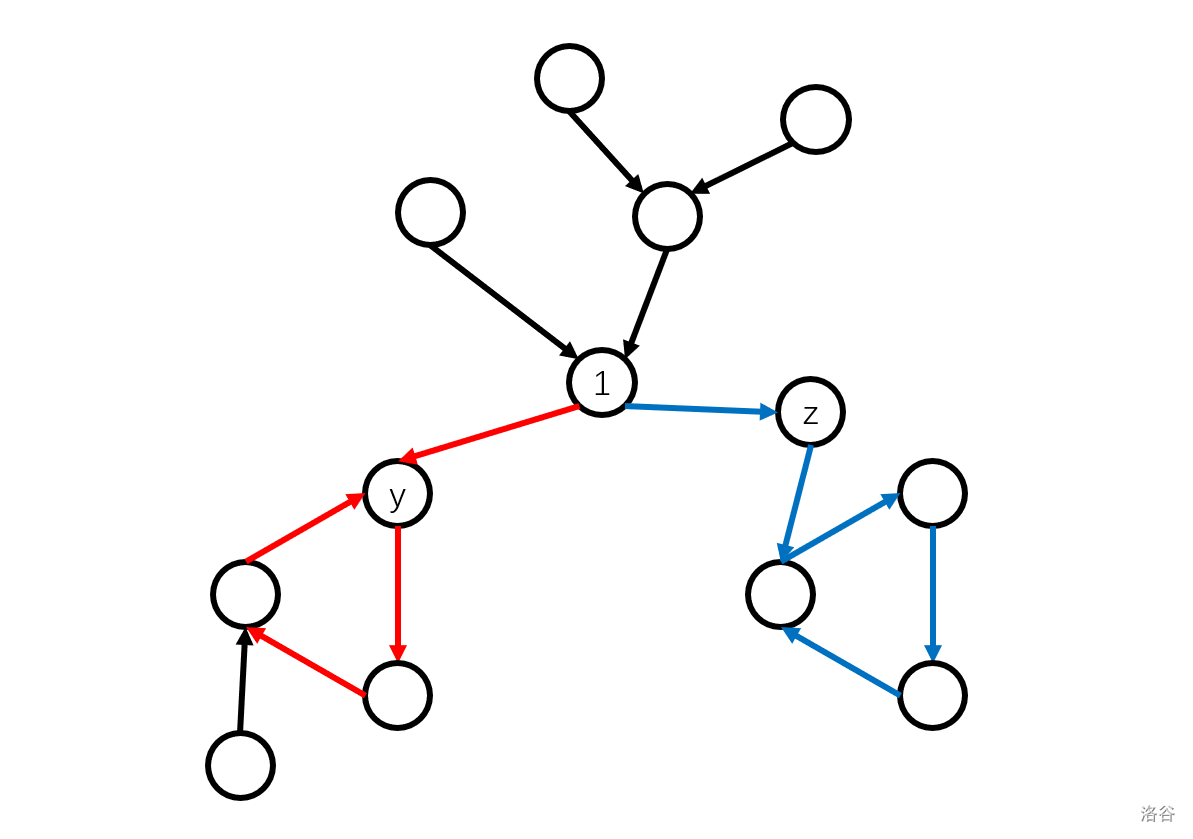
对于这种情况,我们先走到 \(y\),然后沿着继续走,在 \(y\) 所属的基环树上绕一圈,再回到 \(1\),现在整张图和初始情况相比就是 \(y\) 所在的基环树的环(红色环)被反向了。
然后再走到 \(z\),同理绕一圈(蓝色环)再回 \(1\)。
然后再走一次 \(y\),再绕一次红色环,这样红色环被绕了两次,就变回最初的方向了,同理再走一次 \(z\),使得蓝色环也回到最初方向。
-
Case 2:两条出边都指向 \(1\) 为根的树内。
如下图左上部分所示:

这种情况我们考虑 \(y,z\) 的 LCA,如果 LCA 恰好是 \(1\),那么按照和 Case 1 相同的方法做就是没有问题的。
否则我们换一种构造:首先走到 \(y\),然后沿着树上路径走到 \(x\),也就是绕了右上图的红色环。
然后走到 \(z\),沿着树上路径走到 LCA,再从 LCA 走回 \(y\),再走 \(y\to x\) 这条边,如左下图的蓝色环。
最后从 \(x\) 沿树上路径走到 LCA,再从 LCA 走到 \(z\),再走 \(z\to x\) 这条边,如右下图的红色环,构造完成。
证明比较简单,注意图中 \(y,z\) 是动态变化的,在实现的时候,构造过程中的 \(y,z\) 始终是 \(x\) 的出边指向的点。
那么 \(1\) 的出度 \(\ge 2\) 的情况已经证完了,下面考虑 \(1\) 的出度 \(=1\) 的情况。
这时我们只能走这条出边,设为 \(1\to x\),之后 \(1\) 就可以看出零出度点(只要在不走 \(x\to 1\) 这条反向边的情况下回到 \(1\) 就寄了),所以我们删去点 \(1\),同样这也会导致连锁反应,还是用一个拓扑排序就可以把所有该删的点都删了。
在剩下的新图上,把 \(x\) 看成起点继续做即可,即如果 \(x\) 的出度 \(\ge 2\) 那么按照上面方法得到构造;如果 \(x\) 的出度 \(=1\) 那么再走它的出边,然后把 \(x\) 删掉,以此类推。
时间复杂度应该可以做到 \(O(N+M)\),不过我在实现时为了图省事,在记录边的序号以及删点的时候用到了 multiset 和 map,复杂度为 \(O(N+M\log M)\)。
锐评环节
D1T1:比较简单的题,大概是想到单调性之后随便 DP 一下就行了,不过如果没想明白的话可能会用线段树去维护,其实是不用的。
D1T2:人类智慧题,有点看运气,运气好就想出来罢了,主要是到 \(X=26\) 那一步比较有难度,后面的使用其他进制并 DP 以及掐头去尾其实都不是很难。
D1T3:偏简单题,主要是想到用区间表示每个点的状态,后面的数据结构部分非常简单。
D2T1:诈骗题,猜出结论就没有难度了,而想到去猜这个结论其实并不很难(正如我前面所说,如果没有这种结论,这题是不可做的)。
D2T2:中档题,每一步优化都不是很难,但是只要少一步就做不出来,然后最后还要为了零点零几分在那卡常。
D2T3:思维简单,代码不太好写题,感觉这题口胡起来非常舒服。
标签:结点,2022,题解,可以,leq,如果,IOI,垒球,区间 From: https://www.cnblogs.com/ix35/p/16582891.html