第二章 数据结构二

Trie树(字典树)

Trie树，又称字典树，是用来高效存储和查找字符串集合的一种数据结构查找时，可以高效的查找某个字符串是否在Trie树中出现过，并且可以查找出现了多少次

其逻辑结构如下：假设我们需要维护一个字符串集合，它需要支持两种操作

• 向集合插入一个字符串x
• 查询一个字符串在集合中出现了多少次

假设我们有一个字符串集合，包含如下的字符串 ：

abcd，abc，aced，bbac，abde，bcac

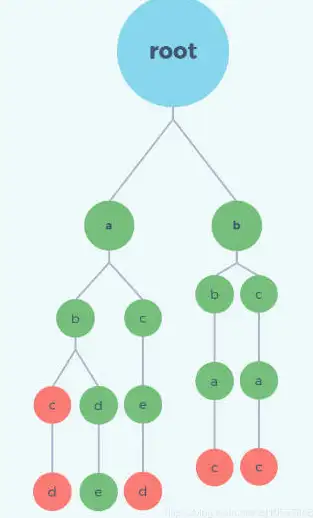
代码模板

const int N = 100010;

int son[N][26], cnt[N], idx; // 下标为0的结点既是根节点，又是空结点

void insert (char str[]) {
    int p = 0;
    for (int i = 0; str[i]; i++) {
        int u = str[i] - 'a';
        if (!son[p][u]) son[p][u] = ++idx;
        p = son[p][u];
    }
    cnt[p]++;
}
int query (char str[]) {
    int p = 0;
    for (int i = 0; str[i]; i++) {
        int u = str[i] - 'a';
        if (!son[p][u]) return 0;
        p = son[p][u];
    }
    return cnt[p];
}

并查集

并查集结构能够支持快速进行如下的操作：

1. 将两个集合合并
2. 询问两个元素是否在一个集合当中并查集可以在近乎O(1)的时间复杂度下，完成上述2个操作

并查集的基本原理：用树的形式来维护一个集合。用树的根节点来代表这个集合。对于树中的每个节点，都存储其父节点的编号。比如一个节点编号为x，我们用p[x]来表示其父节点的编号当我们想求，某一个节点所属的集合时，找到其父节点，并一直往上找，直到找到根节点，则根节点的编号，就是该节点所属的集合的编号。

问题1：如何才能判断根节点

对于根节点x，我们设置p[x] = x。那么，可以用p[x] == x 来判断是否是根节点

问题2：如何求x的集合编号

while(p[x] != x) x = p[x]; 一直向上走，直到找到根节点

问题3：如何合并两个集合

直接将一个集合根节点作为另一个集合根节点的一个子节点即可。

优化：

• 路径压缩：对于查找某个节点x的所属集合，时间复杂度一开始可能没有O(1)，可能需要O(logn)，如果是二叉树的话。但可以采用路径压缩进行优化，当搜索完某个节点的所属集合时，直接将搜索路径上的所有节点的父节点，直接指向根节点，这样下次查询时就是O(1)。
• 按秩合并：用的比较少

代码模板

// 朴素并查集
    int p[N]; //存储每个点的祖宗节点

    // 返回x的祖宗节点
    int find(int x)
    {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }

    // 初始化，假定节点编号是1~n
    for (int i = 1; i <= n; i ++ ) p[i] = i;

    // 合并a和b所在的两个集合：
    p[find(a)] = find(b);

// 维护size的并查集：
    int p[N], size[N];
    //p[]存储每个点的祖宗节点, size[]只有祖宗节点的有意义，表示祖宗节点所在集合中的点的数量

    // 返回x的祖宗节点
    int find(int x)
    {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }

    // 初始化，假定节点编号是1~n
    for (int i = 1; i <= n; i ++ )
    {
        p[i] = i;
        size[i] = 1;
    }

    // 合并a和b所在的两个集合：
    size[find(b)] += size[find(a)];
    p[find(a)] = find(b);

// 维护到祖宗节点距离的并查集：
    int p[N], d[N];
    //p[]存储每个点的祖宗节点, d[x]存储x到p[x]的距离

    // 返回x的祖宗节点
    int find(int x)
    {
        if (p[x] != x)
        {
            int u = find(p[x]);
            d[x] += d[p[x]];
            p[x] = u;
        }
        return p[x];
    }

    // 初始化，假定节点编号是1~n
    for (int i = 1; i <= n; i ++ )
    {
        p[i] = i;
        d[i] = 0;
    }

    // 合并a和b所在的两个集合：
    p[find(a)] = find(b);
    d[find(a)] = distance; // 根据具体问题，初始化find(a)的偏移量

堆

堆的基本操作（以小根堆为例）

1. 插入一个数
2. 求集合当中的最小值
3. 删除最小值
4. 删除任意一个元素
5. 修改任意一个元素堆的基本结构是一颗完全二叉树。以小根堆为例，每个节点都要小于其左右两个子树种的所有节点。

通常用数组来模拟存储一颗二叉树，采用二叉树层序遍历的方式作为数组的下标。若数组下标从0开始，若某个节点下标为x，则其左儿子下标为2x + 1，其右儿子下标为2x + 2。若数组下标从1开始，若某个节点下标为x，则其左儿子下标为2x，右儿子下标为2x + 1。

堆通过下滤（down） 和上滤（up） 来维持堆的特性。

down操作用来将一个较大的数，下沉到合适的位置

up操作用来将一个较小的数，上浮到合适的位置

可以通过down和up操作，完成上述的5个堆的基本操作（数组下标从1开始）

• 插入一个数

插入到数组末尾，并对于新插入的这个数，向上调整

heap[++size] = x; up(size);

• 求集合当中的最小值

直接返回堆顶，即数组的首元素heap[1]

• 删除最小值

先交换堆顶和堆尾，然后堆的大小减一，再针对新的堆顶，向下调整

swap(heap[1], heap[size]); size--; down(1)

• 删除任意一个元素

交换当前元素和堆尾，然后堆的大小减一，再根据新的当前元素的大小，决定是做down操作还是做up操作

swap(heap[i], heap[size]); size--; down(i) 或者 up(i)

• 修改任意一个元素

直接修改，并且根据修改后的新值，来决定做down还是up

heap[i] = x; down(i) 或者 up(i)

代码模板

// h[N]存储堆中的值, h[1]是堆顶，x的左儿子是2x, 右儿子是2x + 1
// ph[k]存储第k个插入的点在堆中的位置
// hp[k]存储堆中下标是k的点是第几个插入的
int h[N], ph[N], hp[N], size;

// 交换两个点，及其映射关系
void heap_swap(int a, int b)
{
    swap(ph[hp[a]],ph[hp[b]]);
    swap(hp[a], hp[b]);
    swap(h[a], h[b]);
}
// 下滤
void down (int u) {
    int t = u;
    if (u * 2 < size && h[2 * u] < h [u]) t = 2 * u;
    if (u * 2 + 1< size && h[2 * u + 1] < h [u]) t = 2 * u + 1;
    if (u != t) {
        heap_swap(u, t);
        down(t);
    }
}
// 上滤
void up (int u) {
    while (u / 2 && h[u] < h[u / 2]) {
        heap_swap(u, u / 2);
        u /= 2;
    }
}
for (int i = n / 2; i > 0; i--) down(i);