第二章 数据结构一

链表

用数组模拟链表(链式向前星）

分类：

1. 单链表，最主要用单链表写邻接表，用邻接表存储图或者树
2. 双链表，优化某些问题

• 对于单链表，开2个数组val[N],nxt[N]，其中val用来存每个链表节点的值，另1个数组nxt用来存每个节点的next指针。

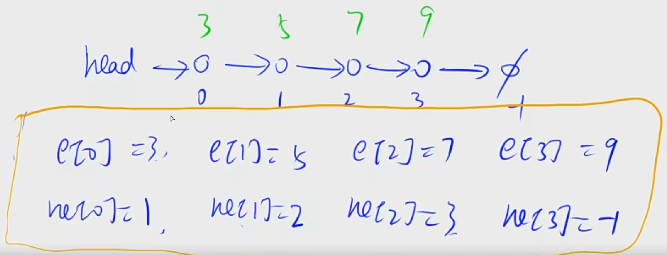
用数组模拟静态单链表代码

int N = 1e5 + 10;
int val[N], nxt[N], head, idx;

void init () {
    head = -1;
    idx = 0;
}
// 将x插到链表头部
void add_to_head (int x) {
    val[idx] = x, nxt[idx] = head, head = idx, idx++;
}
// 将x插入到下标为k的点的后面
void add_after_k (int k, int x) {
    val[idx] = x;
    nxt[idx] = nxt[k];
    nxt[k] = idx;
    idx++;
}
// 删除下标为k的节点的后一个节点
void del_after_k (int k) {
    nxt[k] = nxt[nxt[k]];
}
// 删除头节点
void remove_head () {
    head = nxt[head];
}

• 双链表，开3个数组val[N]，pre[N]，nxt[N]，其中1个用来存每个链表节点的值，另外2个数组用来存每个节点的prev和next指针
• 用数组模拟静态双链表代码

// val[]表示节点的值，pre[]表示节点的左指针，nxt[]表示节点的右指针，idx表示当前用到了哪个节点
int val[N], pre[N], nxt[N], idx;
// 初始化
void init () {
    // 0 代表左端点，1 代表右端点
    nxt[0] = 1, pre[1] = 0;
    idx = 2;
}
// 在下标k的节点的右边插入一个节点
void add_after_k (int k, int x) {
    val[idx] = x;
    nxt[idx] = nxt[k];
    pre[idx] = k;
    pre[nxt[k]] = idx;
    nxt[k] = idx;
}
// 在下标k的节点的左边插入一个节点
void add_before_k (int k, int x) {
    add_after_k(pre[k], x);
}
// 删除第k个节点
void remove (int k) {
    nxt[pre[k]] = nxt[k];
    pre[nxt[k]] = pre[k];
}

栈和队列

用数组模拟栈代码

const int N = 1e5 + 10;
int stack[N];
int top;

void push(int x) { stack[++top] = x; }

void pop() { top--; }

int top() { return stack[top]; }

bool empty() { return top <= 0; }

用数组模拟队列代码

const int N = 1e5 + 10;
int queue[N];
int head = 0, tail = -1;

void push(int x) { queue[++tail] = x; }

void pop() { head++; }

bool empty() { return head > tail; }

int front() { return queue[head]; }

单调栈

应用场景：给定一个序列，对于序列中的每个数，求解它左边离他最近且比它小的数（或者右边，或者比它大）

比如对于序列[3, 4, 2, 7, 5]，求解每个数左边最近的且比它小的数（不存在则返回-1），答案是[-1, 3, -1, 2, 2]对于这个问题，对于第i个元素，假设j < k < i如果a[k] < a[j] 那么a[j] 绝对不会是i的答案，即栈中的元素都是单调的，即若j < k，且a[j] >= a[k]，则往栈中压入1时，会删除先前压入的a[j]。最后保证栈中的元素是升序排列的。

用数组实现单调栈

常见模型：找出每个数左边离它最近的比它大/小的数
int top = 0;
for (int i = 1; i <= n; i ++ )
{
    while (top && check(stk[top], i)) top -- ;
    stk[ ++ top] = i;
}

用slt stack实现单调栈

常见模型：找出每个数左边离它最近的比它大/小的数
stack<int> stk;
for (int i = 1; i <= n; i ++ )
{
    while (stk.empty() && check(stk.top(), i)) stk.pop ;
    stk.push(i);
}

单调队列

最经典的应用：求解滑动窗口中的最大值和最小值

也是先想一个暴力的做法，然后考虑一下能删掉那些元素，是否能得到单调性。

练习题：Acwing - 154: 滑动窗口

代码

#include<iostream>using namespace std;

const int N = 1e6 + 10;

int n, k;
int a[N], q[N];

int main () {
    scanf("%d%d", &n, &k);
    for (int i = 0; i < n; i++) scanf("%d", &a[i]);
    int hh = 0, tt = -1;
    for (int i = 0; i < n; i++) {
        // 判断队头是否已经滑出了窗口
        while (hh <= tt && q[hh] < i - k + 1) hh++;
        while (hh <= tt && a[q[tt]] >= a[i]) tt--;
        q[++tt] = i;
        if (i >= k - 1) printf("%d ", a[q[hh]]);
    }
    puts("");
    hh = 0, tt = -1;
    for (int i = 0; i < n; i++) {
        // 判断队头是否已经滑出了窗口
        while (hh <= tt && q[hh] < i - k + 1) hh++;
        while (hh <= tt && a[q[tt]] <= a[i]) tt--;
        q[++tt] = i;
        if (i >= k - 1) printf("%d ", a[q[hh]]);
    }
    puts("");
    return 0;
}

这道题的思路和上面的单调栈思路类似。注意队列里存放的是下标，而不是数组元素的值。这是因为随着窗口的滑动，需要移除左边的元素，此时存放下标会更加方便。

KMP

模板

#include<iostream>using namespace std;
const int N = 1e5 + 10, M = 1e6 + 10;

char s[M], p[N];

int nxt[N]; //next 数组

int m, n;

int main () {
    // 字符串的起始下标从1开始, 方便处理边界
    cin >> n >> p + 1 >> m >> s + 1;

    // 求解next数组
    for (int i = 2, j = 0; i <= n; i++) {
        while (j && p[i] != p[j + 1]) j = nxt[j];
        if (p[i] == p[j + 1]) j++;
        nxt[i] = j; 
    }
    // KMP匹配过程
    for (int i = 1, j= 0; i <= m; i++) {
        while (j && s[i] != p[j + 1]) j = nxt[j];
        if (s[i] == p[j + 1]) j++;
        if (j == n) {
            // 匹配成功
            printf("%d", i - n + 1);
            j = nxt[j];
        }
    }
    return 0;
}