题目
有 \(n\) 个圆心在 \(x\) 轴上的不相交的圆(存在边界重合),求这些圆将平面分为几部分。
保证 \(1 \leq n \leq 3 \times 10^5\),\(-10^9 \leq x_i,y_i \leq 10^9\)。
一个圆一定将平面(无论它被多少个圆嵌套)分为两部分,我们考虑什么时候这个圆会有额外的贡献。
solution
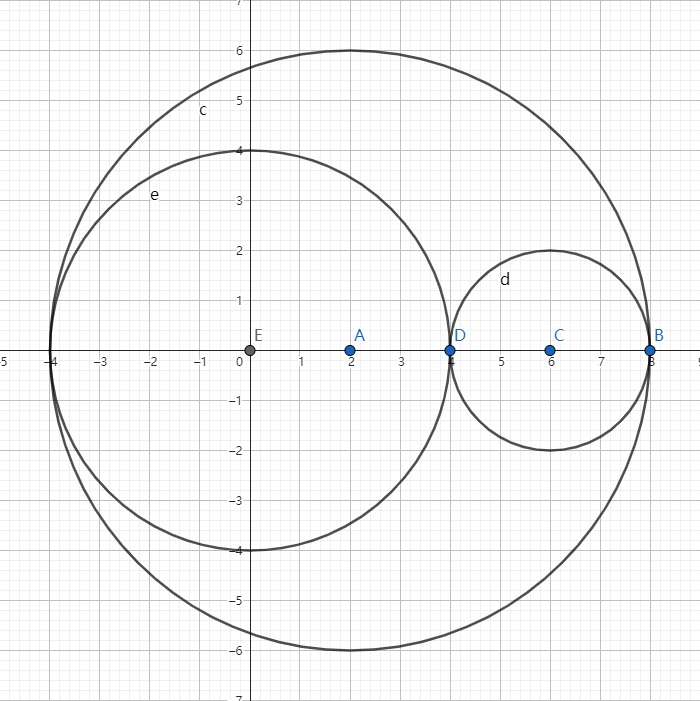
很容易想到一种情况:
此时,两个在大圆中的圆将大圆分割出了额外的一份,贡献加一。
于是我们考虑用一个 map 存储一条线段是否出现过,当两个圆左端点相同时查询是否存在另一半可以分割大圆,如果存在答案加一。
于是我们可以将所有圆按照左端点相同时右端点降序排列,左端点不同左端点降序排列的策略排序,这样可以保证每一对嵌套关系相邻,而且方便处理多层嵌套。
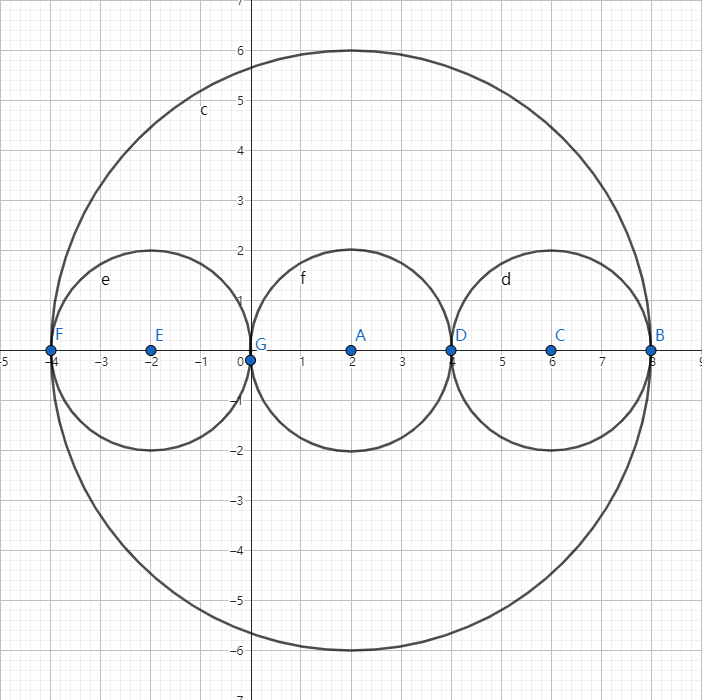
但是还有反例:
如图,此时大圆被三个圆分割,但由于我们一次只处理两个圆,无法统计这种贡献。
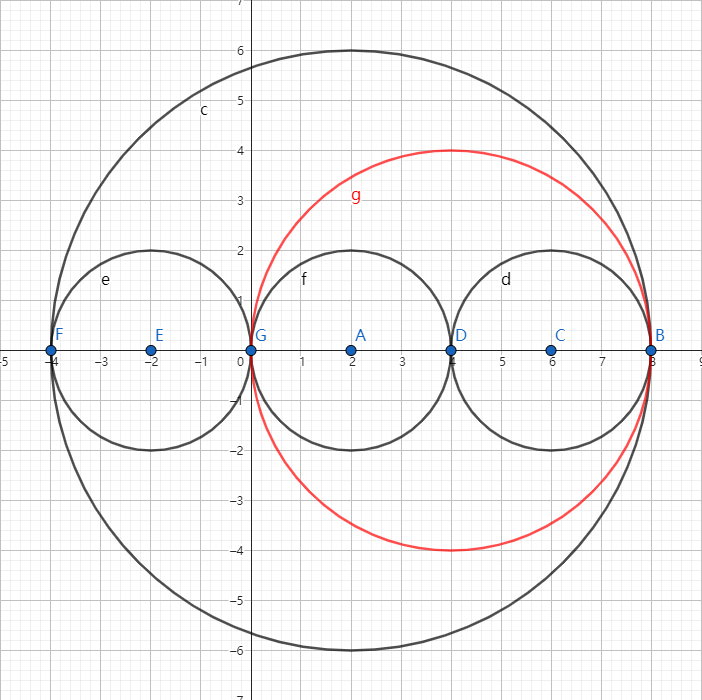
我们考虑虚构一个圆,左端点为小圆的右边界,右端点为大圆的右边界,但不计算他的初始贡献。
此时,当处理到新加入的圆以及圆 \(f\) 时,可以检索到圆 \(d\),贡献被成功计算。
如果新加入的圆无法被分割,由于不计算初始贡献,所以对答案没有影响。
因此,我们需要一个可以快速排序,支持插入的数据结构,堆可以很完美地解决。
点击查看代码
#include<bits/stdc++.h>
#define ull unsigned long long
#define ll long long
#define debug cout<<"DEBUG"<<endl;
#define pb push_back
#define pii pair<int,int>
#define vi vector<int>
#define imp map<int,int>
using namespace std;
const int N=300005;
int n;
struct node{
int l,r;
bool operator<(const node &k)const {
if(l==k.l){
return r>k.r;
}
return l>k.l;
}
}a[N];
priority_queue<node>q;
map<node,int>vis;
ll ans=1;
int main(){
freopen("circle.in","r",stdin);
freopen("circle.out","w",stdout);
cin>>n;
for(int i=1;i<=n;i++){
int x,y;
cin>>x>>y;
a[i].l=x-y;
a[i].r=x+y;
vis[(node){a[i].l,a[i].r}]=1;
q.push((node){a[i].l,a[i].r});
ans++;
}
while(q.size()>1){
node t=q.top();
q.pop();
node t2=q.top();
int l=t.l,r=t.r;
int l2=t2.l,r2=t2.r;
if(l==l2){
if(vis[(node){r,r2}]==1){
ans++;
}else{
q.push((node){r,r2});
}
}
}
cout<<ans<<endl;
return 0;
}