题:力扣
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,
返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
示例 1:
输入: nums = [1,3,5,6], target = 5
输出: 2
示例 2:
输入: nums = [1,3,5,6], target = 2
输出: 1
示例 3:
输入: nums = [1,3,5,6], target = 7
输出: 4
提示:
1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 为 无重复元素 的 升序 排列数组
-104 <= target <= 104
我的原始思路:
由于数组大小排列好了,因此小于数组0位置的数,直接插入,位置0;
大于数组最后一个数的,直接插入,插入位置nums.size();
大小在数组中间,进行二分查找,找到的话输出位置;
没有找到,比大小,夹在中间的输出i+1,即插入的位置。
class Solution {
public:
int searchInsert(std::vector<int>& nums, int target) {
int left = 0;
int right = nums.size() - 1;
int middle = (left + right) / 2;
// 大于数组
if (target < nums[left]) {
return 0;
}
//小于数组
else if (target > nums[right]) {
return right + 1;
}
//在数组之间进行二分查找
else {
while (left <= right) { // 当left==right,区间[left, right]依然有效,所以用 <=
if (nums[middle] == target) {
return middle;
}
else if (nums[middle] > target) {
right = middle - 1; // target 在左区间,所以[left, middle - 1]
}
else {
left = middle + 1; // target 在右区间,所以[middle + 1, right]
}
middle = (left + right) / 2;
}
// 未找到目标值,插入位置
for (int i = 0; i < nums.size() - 1; i++) {
if (nums[i] < target && target < nums[i + 1]) {
return i + 1;
}
}
}
return -1;
}
};
![]() 编辑
编辑
答案:
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int n = nums.size();
int left = 0;
int right = n - 1; // 定义target在左闭右闭的区间里,[left, right]
while (left <= right) { // 当left==right,区间[left, right]依然有效
int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
if (nums[middle] > target) {
right = middle - 1; // target 在左区间,所以[left, middle - 1]
} else if (nums[middle] < target) {
left = middle + 1; // target 在右区间,所以[middle + 1, right]
} else { // nums[middle] == target
return middle;
}
}
// 分别处理如下四种情况
// 目标值在数组所有元素之前 [0, -1], return left=0 or right + 1=0
// 目标值等于数组中某一个元素 return middle;二分法中返回
// 目标值插入数组中的位置 [left, right],return left or right + 1
// 目标值在数组所有元素之后的情况 [left, right], 因为是右闭区间,所以 return left or right + 1
return right + 1; //or return left
}
};- 时间复杂度:O(log n)
- 空间复杂度:O(1)
解析:
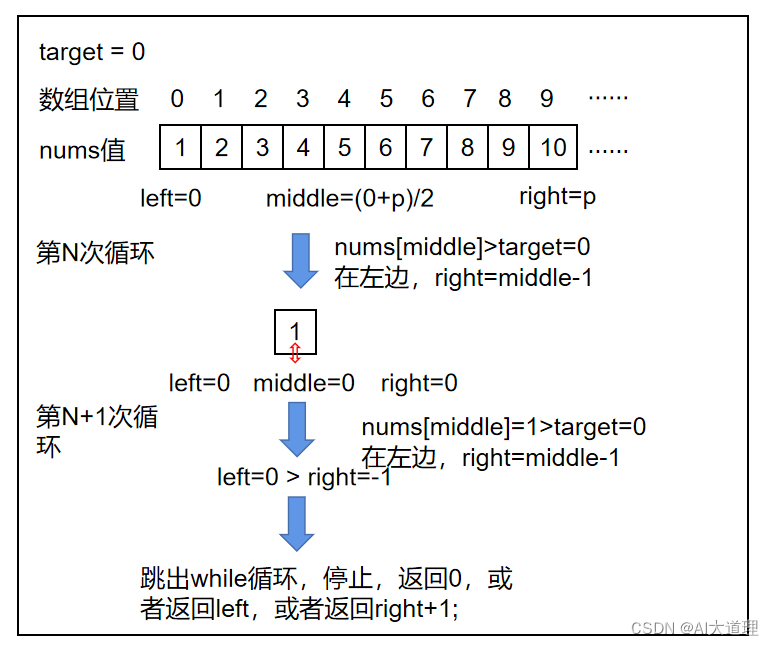
(1)目标值在数组所有元素之前,二分法会使得区间的right一直左移,直到越过了left才停止,最终变为 [0, -1],right=-1跳出循环。返回值0,可用left或者right+1代替。 (我是直接返回了0,后来发现一个巧妙的共同输出。)且left>right,left-right=1。
![]() 编辑
编辑
(2)目标值等于数组中某一个元素,在二分法中返回 middle,与外围的right+1无关。
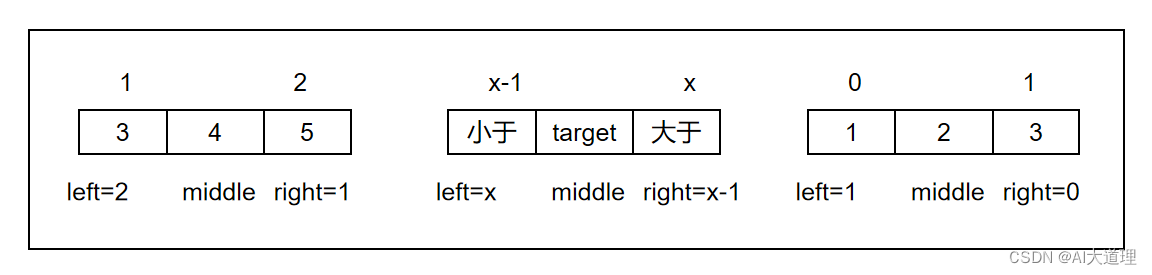
(3)目标值插入数组中的位置,target不是数组中的一个,二分法最后是[left, right],且left>right,left-right=1。返回left或者right + 1。
left等于比target大的第一个数的位置,这个位置就是要插入的位置,right等于比target小的第一个数的位置。
因为总是会归于这么一个情况,即比这个target小,再循环一次,跳到比这个target大的数。
或者比这个target大,再循环一次,跳到比这个target小的数。不管哪种情况,left=x>right=x-1。
(更本质的是因为在倒数第二次的循环中,不是在左边就是在右边,且middle不是等于left就是等于right,然后继续循环一次,导致left+1或者right-1,由于target是两个数之间的一个数,因此跳过了也还没找到target,然后就跳出了循环,得出没找到的结论。)
![]() 编辑
编辑
![]() 编辑
编辑
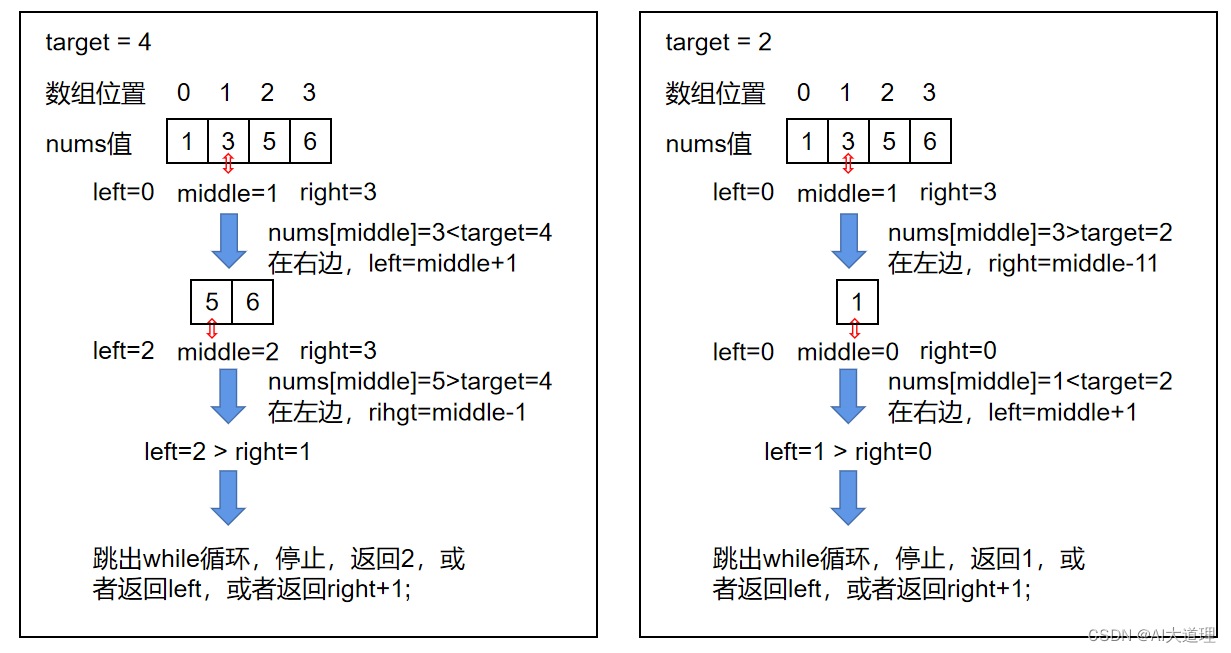
(4)目标值在数组所有元素之后的情况,[left=right+1,right]。left一直右移,直到left+1越过right,跳出循环,即left=right+1,right=numas.size()-1。插入的位置就是left或者说right+1。
总结:
四种情况,除了数组内有和target一样的值的情况返回middle,其他三种情况均可用一个left或者right+1表示。
其他解法:
非二分法,暴力解法。
时间复杂度为O(n),时间复杂度不符合题目要求。
空间复杂度:O(1)
class Solution {
public:
int searchInsert(std::vector<int>& nums, int target) {
for(int i = 0; i < nums.size();i++) {
// 大于或者等于target的num[i],那么i就是结果
if(nums[i] >= target){
return i;
}
}
return nums.size(); //target是最大的
}
};
python:
class Solution:
def searchInsert(self, nums: List[int], target: int) -> int:
left = 0
right = len(nums) - 1
middle = (left + right) // 2
while (left <= right):
if nums[middle] == target:
return middle
elif nums[middle] > target:
right = middle - 1
else:
left = middle + 1
middle = (left + right) // 2
return left