代码随想录 | Day5 | LC 349. 两个数组的交集、202. 快乐数

349. 两个数组的交集

解法1 set去重、contains比较

class Solution {
    public int[] intersection(int[] nums1, int[] nums2) {
        Set<Integer> set1 = new HashSet<>();//使用set集合的方式是通过其子类hashset
        Set<Integer> set2 = new HashSet<>();//注意给好泛型
        //-----int转set(双数组去重)-----
        for (Integer i : nums1) {
            set1.add(i);
        }
        for (Integer i : nums2) {
            set2.add(i);
        }
        //-----取出相同元素存list-----
        List<Integer> list = new ArrayList<>();
        for (Integer i : set2) {
            if (set1.contains(i)) {
                list.add(i);
            }
        }
        //-----list转int输出-----
        int[] ints = new int[list.size()];
        int j = 0;
        for (Integer i : list) {
            ints[j++] = i;
        }
        return ints;
    }
}

解法2 充分利用set特性简化代码

class Solution {
    public int[] intersection(int[] nums1, int[] nums2) {
        Set<Integer> set1 = new HashSet<>();
        Set<Integer> set2 = new HashSet<>();

        for (Integer i : nums1) {
            set1.add(i);
        }

        for (Integer i : nums2) {
            if (set1.contains(i)) {
                set2.add(i);//set集合可以去重
            }
        }

        int[] ints = new int[set2.size()];
        int j = 0;
        for (Integer i : set2) {
            ints[j++] = i;
        }
        return ints;
    }
}

解法3 利用addAll、retainAll函数取交集

class Solution {
    public int[] intersection(int[] nums1, int[] nums2) {
        Set<Integer> set1 = new HashSet<>();
        Set<Integer> set2 = new HashSet<>();//{1,2,2,1};{2,2}
        List<Integer> list =new ArrayList<>();
        for (Integer i : nums1) {
            set1.add(i);
        }
        for (Integer i : nums2) {
            set2.add(i);
        }
        list.addAll(set1);//set转List
        list.retainAll(set2);//保留指定集合中也存在的那些元素，即删除指定集合中不存在的那些元素。
        //{1,2,1}{2}
        
        int[] ints = new int[list.size()];
        int j = 0;
        for (Integer i : list) {
            ints[j++] = i;
        }
        
        return ints;
    }
}

解法4: 娱乐解法(记录自己啥也不会的狰狞)

class Solution {
    public int[] intersection(int[] nums1, int[] nums2) {
        Set<Integer> set = new HashSet<>();
        Set<Integer> set2 = new HashSet<>();
        
        for (int i = 0; i < nums1.length; i++) {
            set.add(nums1[i]);
        }//int转set,数组1去重
        for (int i = 0; i < nums2.length; i++) {
            set2.add(nums2[i]);
        }//int转set,数组2去重
        
        list.addAll(set2);//set转list(为了用contains方法)
        set2.clear();//复用set2集合,盛放交集数组
        
        List<Integer> list = new ArrayList<>();
        for (int i = 0; i < list.size(); i++) {
            if (set.contains(list.get(i))) {
                set2.add(list.get(i));//留存下两数组的交集
            }
        }
        
        //-set转int-
        int[] ints = new int[set2.size()];
        int j=0;
        for (Integer s:set2) {//foreach
            ints[j]=s;//遍历赋值
            j++;
        }
        return ints;
    }
}

此题知识点:

• for each循环
• int数组转set,，set数组转int
• HashSet去重

参考资料

​ ACM 选手图解 LeetCode 两个数组的交集 | 编程文青李狗蛋

​ 代码简洁 一种还不错的解法-小鸡炖蘑菇

202. 快乐数

class Solution {

    public int bit_calculate(int n) {//将传入的数进行按位求平方和 例如:传入19,该函数就会返回82;
        int sum = 0;
        while (n > 0) {
            int last_bit = n % 10;//取的当前数的倒数第一位
            sum += last_bit*last_bit;
            int Del_last_bit = n / 10;//删除当前数的倒数第一位
            n = Del_last_bit;//记下处理后的值继续迭代
        }
        return sum;
    }

    public boolean isHappy(int n) {
        List<Integer> list = new ArrayList<>();
        if (n == 0) {//base case
            return false;
        }
        if (n == 1) {
            return true;
        }
        while (n > 1) {//当n==1时,说明快乐数找到了
            n = bit_calculate(n);
            if(list.contains(n)) {//当计算后的结果与set集合里的元素重复了时,说明一定不是快乐数
                break;
            }
            list.add(n);
        }

        return n==1;//由于while的循环退出是二选一的条件,所以这里要判断以下,到底找到没
    }
}

Hash解法的思路:

本题的题眼其实就是明白如何定义什么时快乐数，什么不是快乐数

​ 即：快乐数，最后的迭代的平方和一定等于1（if判断）

​ 非快乐数，最后迭代的平方和一定会有之前的平方和重复（数与数组值是否重复判断，同349交集那题）

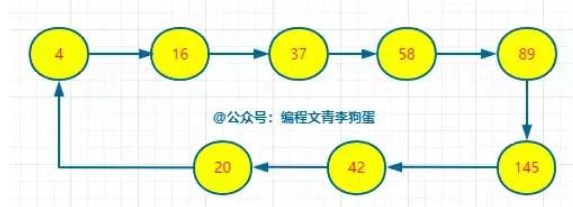
其实就是要读懂题目的无限循环”的意思

​ 什么叫循环，循环就是出现了一遍又一遍，如果循环了那肯定就不是快乐数。

​ 那这道题就可以转化成：【在“将正整数替换为它每个位置上的数字的平方和”过程中，新出现的正整 数是否曾经出现过。】

知识点

• 对一个n位数的数，进行按位的平方求和（怎么写这个函数？）
• 获得上述函数结果，再对其进行按位的求平方和（迭代？）
• （）于我而言，该题反而是进位求和的那题怎么写）

参考资料:

​ ACM 选手图解 LeetCode 快乐数编程文青李狗蛋