P5030 题解

前言

题目传送门！

更好的阅读体验？

一道没啥意思的题目，但是好像很多题解都过不了现在的数据？

思路

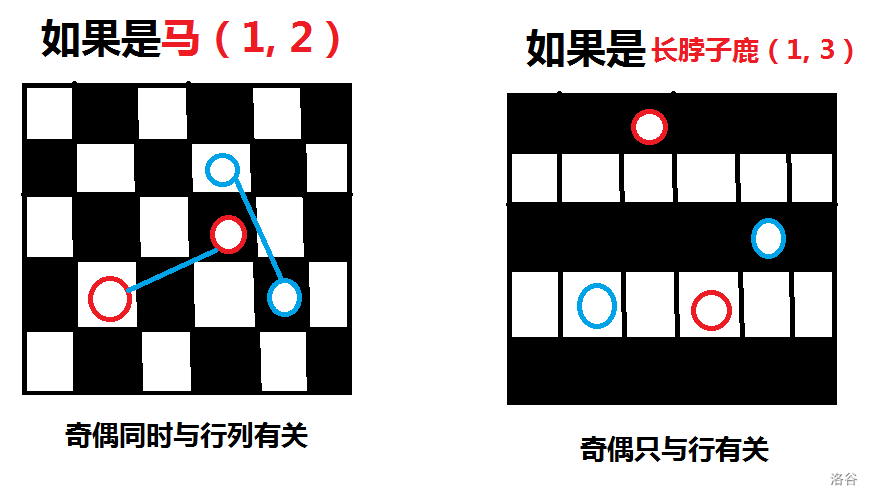
只不过是把正常题目的马（\(1, 2\)）换成了另一种东西（\(1, 3\)）。

很套路地，黑白染色，源点向黑点连边，白点向黑点连边，容量都是 \(1\)。

然后对于两个可以互相到达的点 \((x, y)\) 与 \((dx, dy)\)，如果都没有障碍，那么就连容量是 \(1\) 的边。这里的两个点应该保证颜色不同。

答案即为最大独立集。

本题一个比较不同的点在于黑白染色。正常我们都是按 \((x + y)\) 奇偶性看，而这题我们按 \(x\) 的奇偶性看。

代码

为啥很多题解都过不去？因为更新的数据里，障碍的坐标可能有相同的。

这个也很容易处理，统计时保证不重复即可。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
const int R = 205, N = 114514, inf = 0x7f7f7f7f;
struct Edge {int now, nxt, w;} e[1919810];
int head[N], _head[N], cur = 1;
void ad(int u, int v, int w)
{
    e[++cur].now = v, e[cur].nxt = head[u], e[cur].w = w;
    head[u] = cur;
}
void add(int u, int v, int w) {ad(u, v, w), ad(v, u, 0);}
int s, t;
int dis[N]; bool vis[N];
bool bfs()
{
    queue <int> q;
    memset(vis, false, sizeof vis);
    q.push(s), vis[s] = true, dis[s] = 0, _head[s] = head[s];
    while (!q.empty())
    {
        int u = q.front(); q.pop();
        for (int i = head[u]; i; i = e[i].nxt)
        {
            int v = e[i].now;
            if (vis[v] || !e[i].w) continue;
            vis[v] = true, dis[v] = dis[u] + 1, _head[v] = head[v];
            if (v == t) return true;
            q.push(v);
        }
    }
    return false;
}
int dfs(int u, int maxflow)
{
    if (u == t) return maxflow;
    int flow = 0;
    for (int i = _head[u]; i && flow < maxflow; i = e[i].nxt)
    {
        _head[u] = i;
        int v = e[i].now;
        if (dis[v] != dis[u] + 1 || !e[i].w) continue;
        int ww = dfs(v, min(maxflow - flow, e[i].w));
        if (!ww) dis[v] = -inf;
        e[i].w -= ww, e[i ^ 1].w += ww, flow += ww;
    }
    return flow;
}
int dinic()
{
    int ans = 0, flow;
    while (bfs())
        while (flow = dfs(s, inf))
            ans += flow;
    return ans;
}
int n, m, k; bool a[R][R];
int id(int x, int y) {return (x - 1) * m + y;}
const int dict[8][2] = {{1, 3}, {1, -3}, {-1, 3}, {-1, -3}, {3, 1}, {3, -1}, {-3, 1}, {-3, -1}};
int main()
{
    scanf("%d%d%d", &n, &m, &k);
    s = 0, t = n * m + 1;

    int sum = n * m;
    while (k--)
    {
        int x, y;
        scanf("%d%d", &x, &y);
        if (!a[x][y]) sum--;
        a[x][y] = true;
    }
    for (int x = 1; x <= n; x++)
        for (int y = 1; y <= m; y++)
            if (x & 1) add(s, id(x, y), 1); //按行黑白染色
            else add(id(x, y), t, 1);
    for (int x = 1; x <= n; x++)
        for (int y = 1; y <= m; y++)
            if ((x & 1) && !a[x][y])
                for (int i = 0; i < 8; i++)
                {
                    int dx = x + dict[i][0], dy = y + dict[i][1];
                    if (dx < 1 || dx > n || dy < 1 || dy > m) continue;
                    if (a[dx][dy]) continue;
                    add(id(x, y), id(dx, dy), 1); 
                }
    cout << sum - dinic(); //最大独立集
    return 0;
}

希望能帮助到大家！