Codeforces Round48 Edu题解

A - Death Note（模拟）

题意

​ 现在有一本书，每页可以写下 \(m\) 个数字，给你一个序列 \(a\) ，依次在书上誊写 \(a_i\) 个数字，请问誊写序列的第 \(i\) 个数的时候书翻了几页？

​ \(simple：m = 5, a = {3, 7, 9}\)

​ \([1, 1, 1, 2, 2],[2, 2, 2, 2, 2],[3,3,3,3,3],[3,3,3,3]\)

​ 所以写 1 的时候，没有翻页；写 2 翻两页；写 3 翻一页。

思路

​ 按照题意模拟，对页数取模。

代码

const int N = 200005;
int n, m;
ll a[N];
 
int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i ++)
        cin >> a[i];
 
    ll s = 0, last = 0;
    for(int i = 1; i <= n; i ++)
    {
        a[i] += last;
        s = a[i] % m;
        ll res = a[i] / m;
        cout << res << ' ';
        last = s;
    }
}

B - Segment Occurrences（前缀和）

题意

​ 给出一个字符串 \(s\) 和字符串 \(t\) ，询问 \(10^5\) 次 \(s\) 的区间 \([l,r]\) 内有多少个 \(t\)。

思路

​ 前缀和一下就行，我们用 \(pre_i\) 表示以 \(i\) 作为开头的长度为 \(len\_t\) 的字符串是否和 \(t\) 相等，然后再加上 \(pre_{i-1}\)。查询的时候直接O1就出来了。

代码

const int N = 200005;
string a, b;
int n, m, q;
int pre[N]; //[1, i]中作为开头的适配的子串有多少个。
 
int main()
{
    cin >> n >> m >> q;
    cin >> a >> b;
    a = '#' + a;
 
    for(int i = 1; i <= n; i ++)
    {
        auto t = a.substr(i, m);
        // cout << t << '\n';
        pre[i] = pre[i - 1];
        if(b == t)
            pre[i] ++;
        // cout << pre[i] << '\n';
    }
 
    while(q --)
    {
        int l, r;
        cin >> l >> r;
        if(r - l + 1 < m)
            cout << 0 << '\n';
        else
            cout << pre[r - m + 1] - pre[l - 1] << '\n';
    }
}   

C - Vasya And The Mushrooms（预处理 模拟）

题意

​ 给出一个 2 行 \(n\) 列的地图，地图上的每一个点都有权值。现在你在地图的左上角，要求一笔画地走完整个地图（对于地图上的每个点，只能且必须经过一遍）。当你当前已经走了 \(k\) 步时，走到 \(a_{i,j}\) 上的权值为 \(k \times a_{i,j}\) 。请问如何走能够使权值最大，输出最大的权值和。

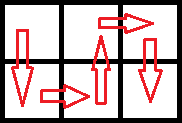
*一笔画如图所示

思路

​ 一开始一定是螺旋着走，然后在某个列开始一路走到最右端，再向上（下）走回头。这种状态一共有 \(n\) 种，但是每次计算也需要 \(O(n)\) ，我们可以发现里面嵌套的 \(O(n)\) 只是在遍历方格并加和，我们尝试是否能通过预处理信息来解决这个问题。在草稿纸上画一个地图上权值全为 1 的地图，然后手玩一下就可以发现是有规律的。这告诉我们打 CF 要敢于找规律...

​ 对于列预处理一个后缀和，然后枚举从哪一列（分奇偶讨论一下）开始向右走，算一下就可以了。下图蓝色部分是会发生变化的部分。

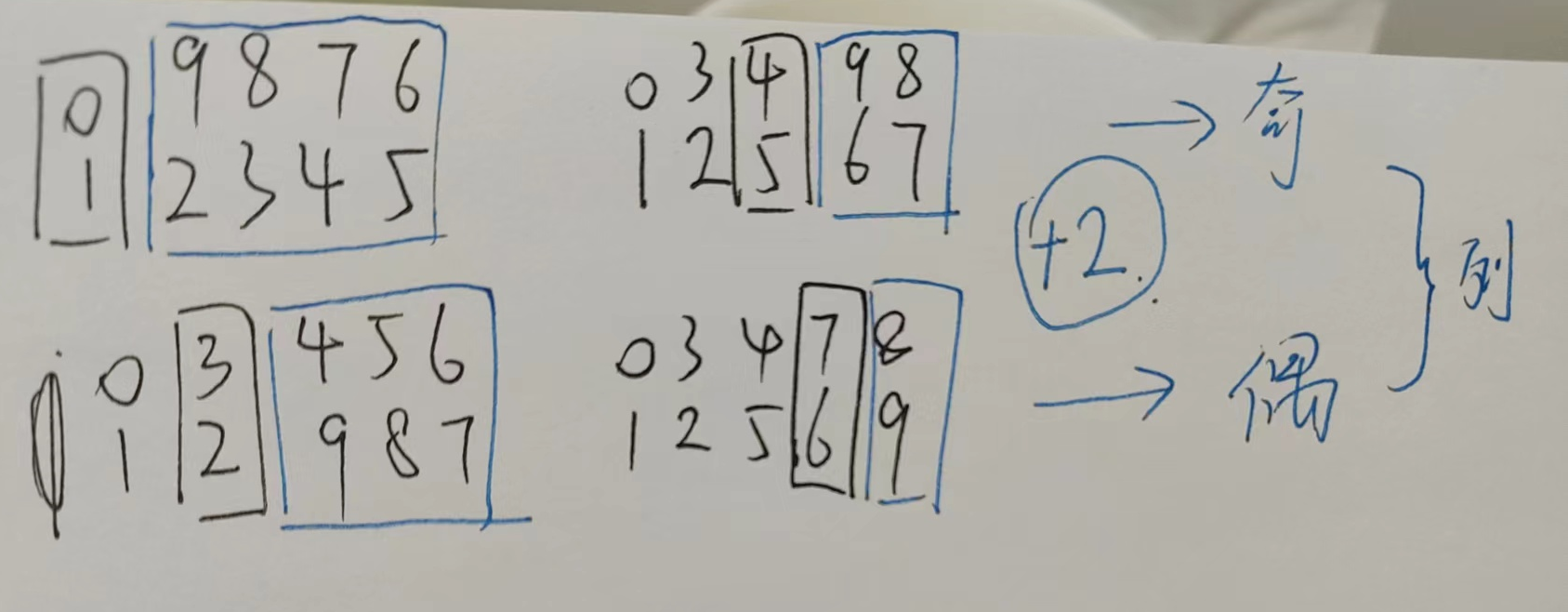
代码

​ 写的比较笨B，但是这是我觉得比较好想的写法。不要忘了第 0 列的情况，也就是从 \((1, 1)\) 就开始往右走。

const int N = 300005;
ll a[2][N];
int n;
 
int main()
{
    cin >> n;
    for(int i = 1; i <= n; i ++)
        cin >> a[0][i];
    for(int i = 1; i <= n; i ++)
        cin >> a[1][i];
 
    vector<ll> pre(n * 2 + 1, 0), last_sum1(n + 2, 0), last_sum2(n + 2, 0); //1是奇数列转折，2是偶数列转折   
    for(int i = 2; i <= 2 * n; i += 2)
    {
        int col = i / 2;
        if(col & 1)
        {
            pre[i - 1] = pre[i - 2] + (i - 2) * a[0][col];
            pre[i] = pre[i - 1] + (i - 1) * a[1][col];
        }
        else
        {
            pre[i - 1] = pre[i - 2] + (i - 2) * a[1][col];
            pre[i] = pre[i - 1] + (i - 1) * a[0][col];
        }
    }
 
    
    ll x, y;
    y = n, x = y + 1;
    for(int i = n; i >= 1; i --)
    {
        last_sum1[i] = last_sum1[i + 1] + (y * a[1][i] + x * a[0][i]);
        x ++, y --;
    }
    y = n + 2, x = n + 1;
    for(int i = n; i >= 1; i --)
    {
        last_sum2[i] = last_sum2[i + 1] + (y * a[1][i] + x * a[0][i]);
        x --, y ++;
    }
 
    vector<ll> last_sum3(n + 2, 0);
    for(int i = n; i >= 1; i --)
        last_sum3[i] = last_sum3[i + 1] + (a[0][i] + a[1][i]);
 
    ll res = 0;
    for(int i = 2, cnt = 0; i <= 2 * n; i += 2)
    {
        int col = i / 2;
        if(col & 1)
        {
            res = max(res, pre[i] + last_sum1[col + 1] + cnt * last_sum3[col + 1]);
        }
        else
        {
            res = max(res, pre[i] + last_sum2[col + 1] + cnt * last_sum3[col + 1]);
            cnt += 2;
        }
    }
    ll s = 0, cnt = 0;
    for(int i = 1; i <= n; i ++)
    {
        s += cnt * a[0][i];
        cnt ++;
    }
    for(int i = n; i >= 1; i --)
    {
        s += cnt * a[1][i];
        cnt ++;
    }
    res = max(res, s);
    cout << res << '\n';
}       

D - Vasya And The Matrix（构造，XOR）

题意

​ 请构造出一个矩阵，其各行异或和为 \(a_1,a_2...a_n\) ，其各列异或和为 \(b_1,b_2...b_m\)。若能构造出这样的矩阵，那么输出YES和矩阵；若无法构造，输出NO。

思路

​ \(n=100\) 的话，误导了我去想很多复杂的算法。其实这题只需要抓住XOR的性质就可以了。易知，我们可以这样判断是否能构造出这样的矩阵：若每一行异或和的异或和等于每一列异或和的异或和，一定存在这样的矩阵；反之一定无法构造出。

​ 又因为 0 和 \(x\) 异或是 \(x\) ，我们直接让每一行中，都由 \(0\) 和 \(a_i\) 构成；每一列中，都由 \(0\) 和 \(b_i\) 构成（除了第 \(n\) 行第 \(m\) 列的位置）。那么易得 \(a_{n,m}=a_1 \oplus ... \oplus a_{n-1} \oplus b_m\) 或者 \(a_{n,m}=b_1 \oplus ... \oplus b_{m-1} \oplus a_n\)

代码

const int N = 105;
int n, m;
int res[N][N];

int main()
{
    cin >> n >> m;
    vector<int> a(n + 1, 0), b(m + 1, 0);
    for(int i = 1; i <= n; i ++)
        cin >> a[i];
    for(int i = 1; i <= m; i ++)
        cin >> b[i];
 
    int xor_a = 0, xor_b = 0;
    for(int i = 1; i <= n; i ++)
        xor_a ^= a[i];
    for(int i = 1; i <= m; i ++)
        xor_b ^= b[i];
 
    if(xor_a != xor_b)
    {
        cout << "NO\n";
        return 0;
    }
 
    for(int i = 1; i <= n - 1; i ++)
        res[i][m] = a[i];
    for(int i = 1; i <= m - 1; i ++)
        res[n][i] = b[i];
    int ans = 0;
    for(int i = 1; i <= n - 1; i ++)
        ans ^= a[i];
    ans ^= b[m];
    res[n][m] = ans;
 
    cout << "YES\n";
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= m; j ++)
            cout << res[i][j] << " \n"[j == m];
}