因子分析的六类应用
大部分情况下，我们所认识与理解的因子分析，就是用个数较少的新变量代替原始变量，并且希望新变量能涵盖原始变量较多的信息即浓缩信息；这是因子分析最常用也是最广为人知的一种用法，但除此之外，因子分析还有几个隐藏用法。
比如还可以使用因子分析进行结构效度分析、综合竞争力分析、权重分析、共同方法偏差检验等，如下图所示：
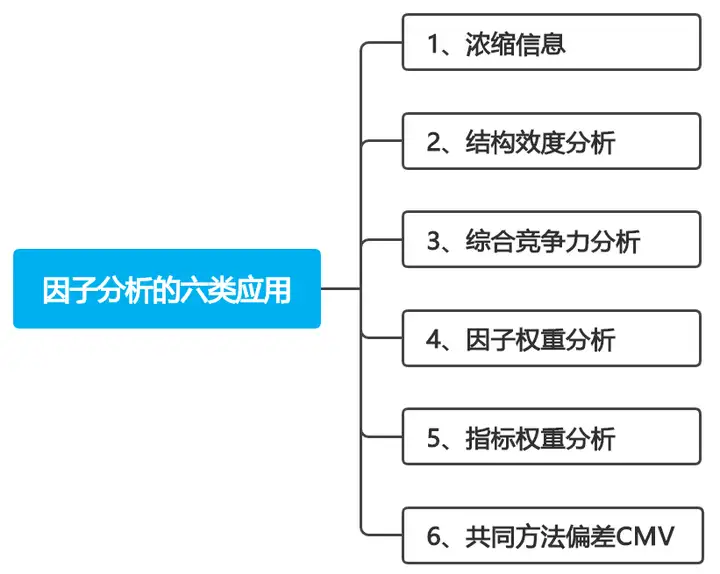
下面，将对因子分析的几类应用进行逐个说明。
（一）浓缩信息
使用因子分析进行信息的浓缩，即将分析项浓缩成几个因子，使用这几个因子能够代表所有分析项的大部分信息。
在浓缩信息时，可以根据专业知识进行因子个数的设置，若不设置，SPSSAU系统将以特征根值大于1作为判断标准设定因子个数。
例如：下面这篇论文中，使用SPSSAU对研学旅行目的地映像进行因子分析，SPSSAU操作步骤如下：
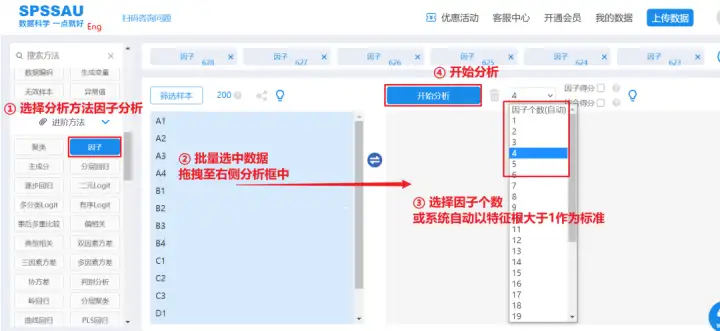
SPSSAU分析结果如下图：可以看出KMO值为0.845，大于0.6，同时巴特球形值对应p值小于0.01；意味着数据适合进行因子分析；对应项之间关系明朗，没有出现 “ 张冠李戴 ” 和 “ 纠缠不清 ” 的情况。
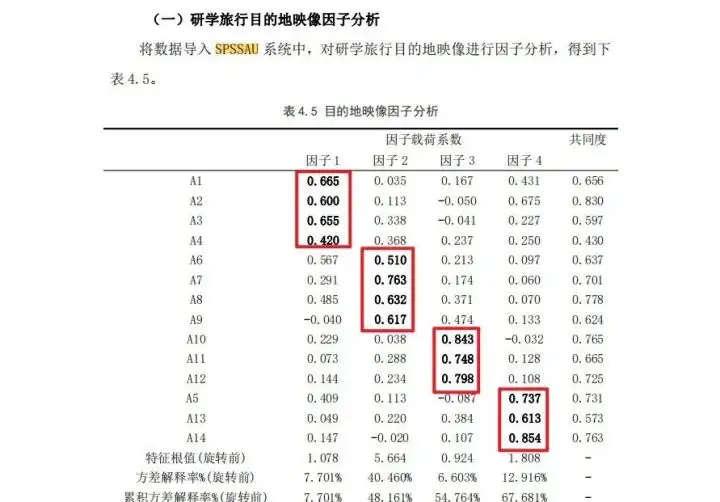
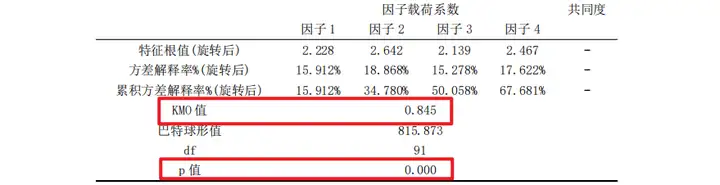
研学旅行目的地选择的影响因素研究-刘畅
可以在分析前选择 “ 保存因子得分 ” ：SPSSAU因子分析将信息浓缩成的几个因子将自动被保存下来，可在选中 “ 因子得分 ” 后在右上角 “ 我的数据 ” 中进行查看；或者可以直接使用浓缩后的因子进行后续分析，例如进行回归分析、聚类分析等使用。
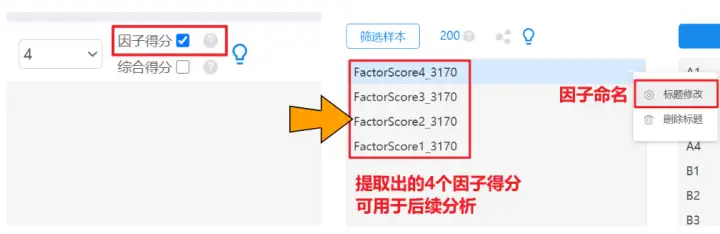
（二）结构效度分析
效度分析（结构效度）反映量表能够正确测量的特质程度，其目的在于检验测量结果准确反映变量的程度即量表题的设计合理性，检验效度最常用的方法是因子分析（探索性因子分析EFA）。
例如：在下面这篇论文中，研究者使用探索性因子分析进行问卷的结构效度研究。
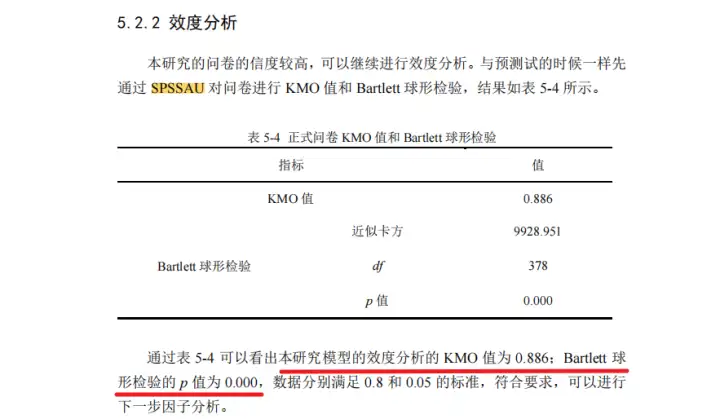
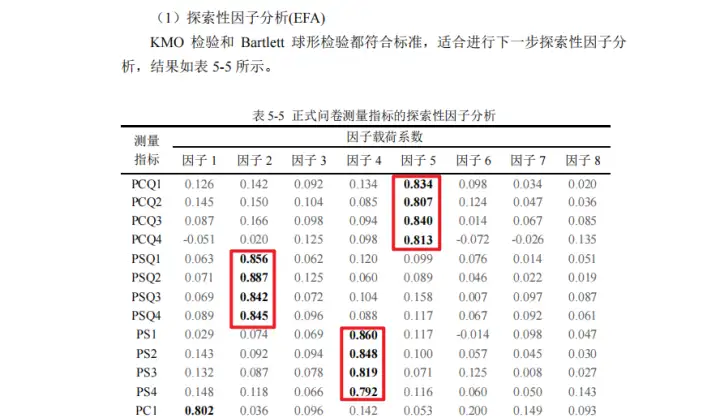
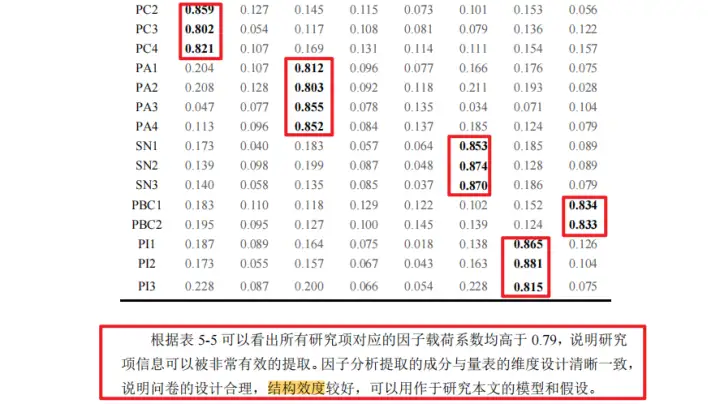
视频网站用户付费意愿影响因素研究-林岩星
在SPSSAU系统中，可以使用进阶方法【因子分析】（探索性因子分析）进行结构效度分析，也可以直接在问卷研究下的【效度分析】进行结构效度分析，二者的分析是一样的。
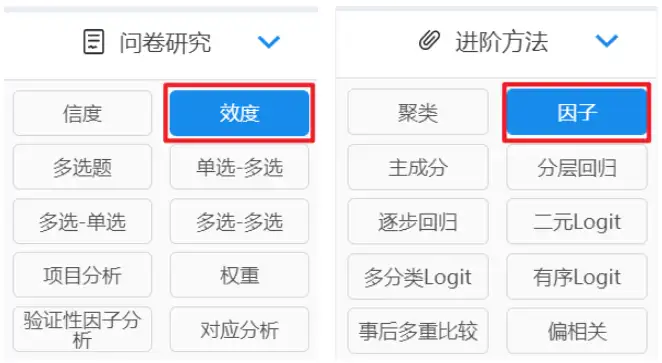
（三）综合竞争力分析
因子分析可以通过SPSSAU生成的综合得分，研究企业的综合竞争力；综合得分值越高，则综合竞争力越强。
综合竞争力研究常见于经济、管理类研究，例如研究上市公司的综合竞争力排名。
开始分析前，选中【综合得分】按钮，SPSSAU将自动生成一列综合得分；
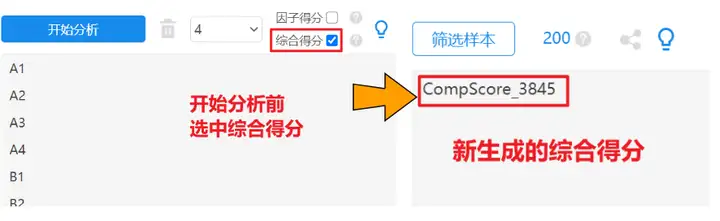
新生成的综合得分可以在右上角我的数据中进行查看，可以将数据下载至本地，然后使用EXCEL对综合得分进行排序，得到综合竞争力排名；或者直接使用SPSSAU系统生成变量功能进行排名（Rank），即可一键得到综合竞争力排名。
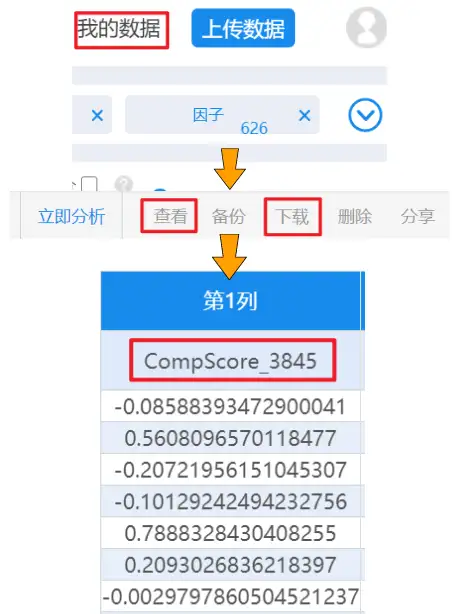
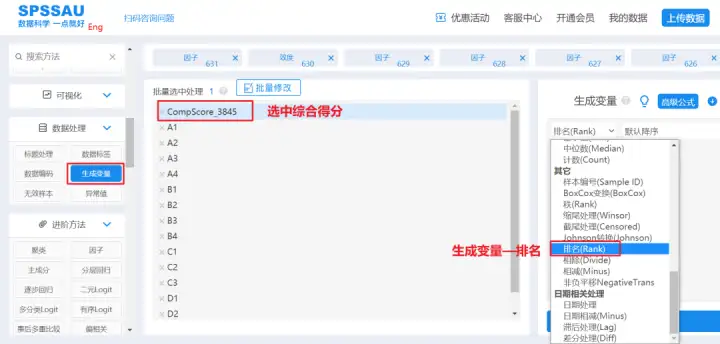
（四）因子权重分析
因子分析提取出因子后，如果想分析各个因子所占权重，可以使用旋转后方差解释率进行因子权重分析。
查看因子分析的 “ 方差解释率 ” 表格，计算因子权重只需要看两个值—各因子旋转后方差解释率和旋转后累计方差解释率。如下图：各因子旋转后方差解释率为26.400%、21.703%、19.013%、15.359%、7.087%；旋转后累计方差解释率为89.563%。
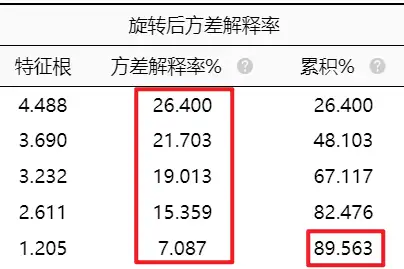
归一化（旋转后方差解释率 / 旋转后累计方差解释率），即可得到各因子权重：
因子1权重=26.400%/89.563%=0.295
因子2权重=21.703%/89.563%=0.242
......
（五）指标权重分析
各个指标的权重也可以使用SPSSAU因子分析得到。
SPSSAU系统在进行因子分析时，自动输出线性组合系数及权重计算结果，找到此表，最后一列即输出各个指标的权重值。
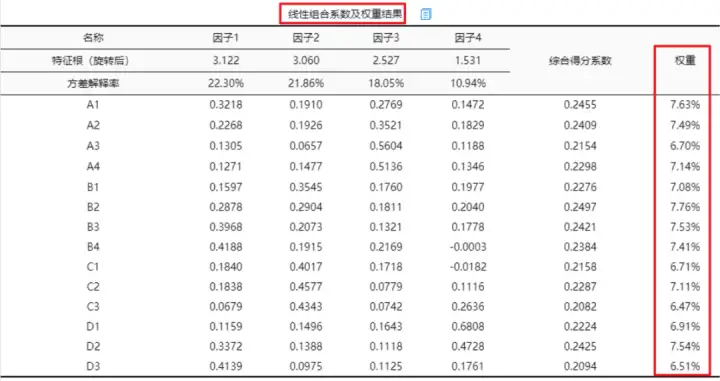
上表中，权重=归一化综合得分系数；
综合得分系数=累积（线性组合系数*方差解释率）/ 累计方差解释率
线性组合系数=载荷系数 / 对应特征根的平方根
虽然计算公式比较复杂，但SPSSAU系统一键即可直接得到计算结果。
（六）共同方法偏差CMV
共同方法偏差是由相同受访者在相同测试环境下填写问卷时，对多个变量进行测量所带来的的偏差。共同方法偏差会显著降低研究结果的可信度，甚至会影响模型检验。
共同方法偏差可以使用Harman单因子检验法；即将所有指标放在一个因子下进行因子分析，如果该因子的方差解释率低于40%（常见标准），则认为研究数据并不存在严重的共同方法偏差，反之，则认为存在共同方法偏差。
SPSSAU操作：
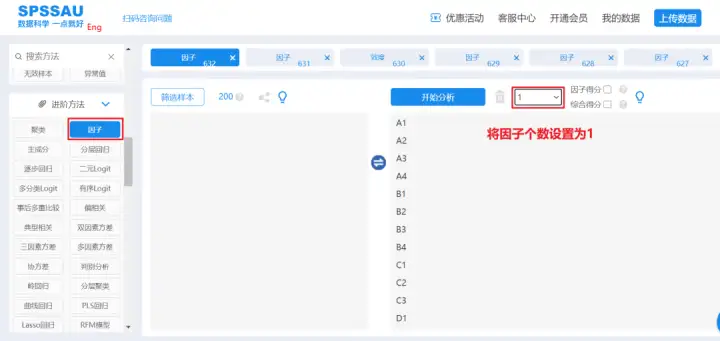
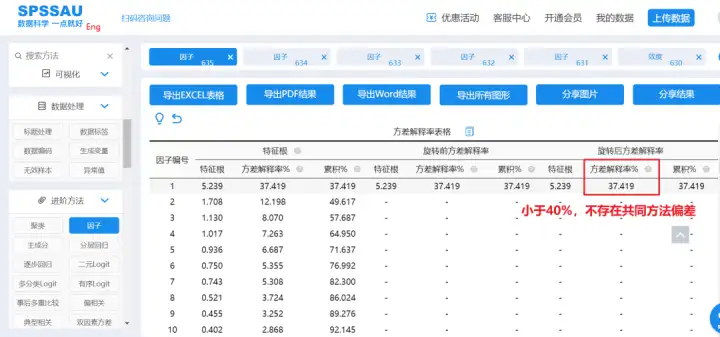
SPSSAU输出结果：
方差解释率为37.419%<40%，说明该研究数据不存在共同方法偏差。
标签：分析,因子分析,方差,因子,SPSSAU,应用,效度,六类
From： https://www.cnblogs.com/spssau/p/17012541.html