title: 最小割
tags: 算法
date: 2022-11-28 13:18:15
本文章遵守知识共享协议 CC-BY-NC-SA ,转载时须在文章的任一位置附上原文链接和作者署名(rickyxrc)。推荐在我的个人博客阅读。
简介
最小割是网络最大流算法的扩展
前置知识
- 网络最大流
讲解
首先给出定律:最小割等于最大流。
好,就这么多。现在去解题吧
顾名思义,最小割是在“割”,即将一个图分成 \(A\) 和 \(B\) 两个集合,其中 \(S\) 可以到 \(A\) 中所有点, \(B\) 中所有点可以到 \(T\) 。这个图的一个割就是指两个集合之间的流量。
这个割的性质可以解许多的题。
例题
P1345-[USACO5.4]奶牛的电信Telecowmunication
这题是一个最小割的应用,简单来说就是将一个点拆成两个,用权为1的边连接,其他正常的边用权为inf连接。
因为最大流等于最小割,所以跑一遍最大流就行了。
for(int i=1;i<=n;i++){
add(i,i+n,1); // 每个点拆成两个点
}
for(int i=1;i<=m;i++){
scanf("%d%d",&u,&v);
add(u+n,v,114514); // 点与点之间的边不能被分割,为inf
add(v+n,u,114514); // 双向跑,因为不知道哪边源点哪边汇点
}
ans = dinic(s,t); // S和T是题目中给出的两个点
P2762 太空飞行计划问题
这道题不容易想到是网络流,所以我们需要考虑转化。
考虑构建如下一个图:
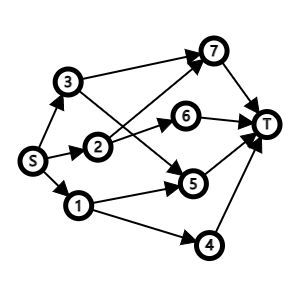
将实验编号为1~m,m+1~m+n,然后源点连接所有实验,所有实验器材连接汇点,根据实验的依赖关系来进行连边。
对于边权,源点连接实验为实验的价值,仪器连接汇点为仪器的费用。
这里可以这么想:我已经拿到了实验的所有利润,然后一次一次割掉仪器或实验来让利润更大。
实验和仪器间的关系肯定不能被割掉,所以这里的边权可以设置为inf。
所以构建完图跑一边最小割即可,核心代码如下。
for (int i = 1; i <= m; i++)
{
scanf("%d", &cost);
sum+=cost;
add(s, i, cost); // 源点连实验
val = 0;
ch=getchar();
while (true)
{
ch = getchar();
if (isdigit(ch))
val = (val * 10) + (ch - '0');
//可以替换成 val = (val<<1) + (val<<3) + (ch^48); (快速读入写法)
else if (ch == ' ')
{
add(i, m + val, inf); // 实验连仪器
val = 0;
}
else if (ch == '\r' || ch == '\n')
{
add(i, m + val, inf); // 实验连仪器
val = 0;
break;
}
}
}
for (int i = 1; i <= n; i++)
{
scanf("%d", &val);
add(m + i, t, val); // 仪器连汇点
}
P2598-[ZJOI2009]狼和羊的故事
分析题目,可以转化为将所有狼和所有羊都不连通的方案。
所以将 \(S\) 连所有羊,所有狼连 \(T\) ,这些边的容量为 \(inf\) (因为不能被割掉)。
此外,对于每个点,都要向四周连容量为 \(1\) 的边,这些才是可以被割掉的。
int calcxy(int i,int j){return i+(j-1)*m;}
scanf("%d%d",&m,&n);
s=n*m+2;t=n*m+1;
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
scanf("%d",&tp);
if(tp == 2)
add(s,calcxy(i,j),inf);
if(tp == 1)
add(calcxy(i,j),t,inf);
}
}
for(int i=1;i<m;i++)
for(int j=1;j<=n;j++)
add(calcxy(i,j),calcxy(i+1,j),1);
for(int i=1;i<=m;i++)
for(int j=1;j<n;j++)
add(calcxy(i,j),calcxy(i,j+1),1);
for(int i=2;i<=m;i++)
for(int j=1;j<=n;j++)
add(calcxy(i,j),calcxy(i-1,j),1);
for(int i=1;i<=m;i++)
for(int j=2;j<=n;j++)
add(calcxy(i,j),calcxy(i,j-1),1);
printf("%d",dinic());