这波乱搞
新年发博客?
不存在,只是开个坑
所以这篇文章干屁用
是 \(hash\), \(kmp\),\(trie\) 树,\(AC\) 自动机的学习笔记
好吧,我基本是深夜更新
话不多说,我们就进入鬼畜奇妙的字符串世界吧
1.HASH,哈希
此算法可能是最简单的了
我们就时将每个字符串看成 \(base\) 进制的数,然后比较哈希值,但是呢,我们一个个转换后相加会很容易爆炸,所以我们需要对 \(mod\) 取余
不过这个 \(mod\) 最好取孪生素数,不然就会被毒瘤出题人卡掉
下面给出代码
const ull base = 233;
const ull mod = 1e9 + 5;
inline ull hash(char s[]) {
int len = strlen(s);
ull sum = 0;
for (int i = 0; i < len; i ++)
sum = (sum * base + (ull)(s[i])) % mod;
return sum;
}
接下来我门来看看 \(P3370\)
其实是模板题
只要算出每一个字符串的哈希值,然后从小到大排序,比较即可
注意,对于孪生素数,这里的数据卡掉了\(1e9+7\)
代码如下
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define ull unsigned long long
const int N = 1e5 + 7;
const ull base = 233;
const ull mod = 1e9 + 5;
using namespace std;
ull a[N];
char s[N];
int n, ans = 1;
inline ull hash(char s[]) {
int len = strlen(s);
ull sum = 0;
for (int i = 0; i < len; i ++)
sum = (sum * base + (ull)(s[i])) % mod;
return sum;
}
inline bool cmp(int x, int y) {
return x < y;
}
int main() {
cin >>n;
for (int i = 1; i <= n; i ++) {
scanf("%s", s);
a[i] = hash(s);
}
sort(a + 1, a + 1 + n, cmp);
for (int i = 1; i < n; i ++) {
if (a[i] != a[i + 1])
ans ++;
}
cout << ans << endl;
return 0;
}
例题的话,这里先给几道,有机会再更
\(1.\) UVA10298 Power Strings
2.KMP
怎么说呢
这东西是挺好玩的
主要是给你个字符串 \(A\) 和 \(B\),叫你求 \(B\) 在 \(A\) 中出现了几次
\(In\) \(a\) \(word\),就是字符串匹配
其实 \(hash\) 也可以,\(but\) \(as\) \(we\) \(know\),会被毒瘤出题人(noip) 卡
于是就诞生了 \(kmp\) 这破烂好玩意
我们要先理解一个叫做 前缀数组 和 后缀数组 的玩意
前缀数组呢,就是一个字符串这东西,他的前缀,类似于
abcdb
前缀数组:a, ab, abc, abcd, abcdb
后缀数组就是反着来,类似于
abcdb
后缀数组:b, db, cdb, bcdb, abcdb
那么我们的 \(nxt_i\) 就是在第 \(i\) 位的时候他的 前缀和 后缀 长度
类似于
ababd
先是a这个,那么nxt[1] = 0
然后ab,那么明显的nxt[2] = 0
接着是aba,那么都有a,所以nxt[3] = 1
然后是abab,那么前后缀都有ab,所以nxt[4] = 2
然后是ababd,没有相同的前缀后缀,所以nxt[5] = 0
所以abcdb的nxt数组为
0 0 1 2 0
主要是如何求
明显暴力
要是暴力就没那么有名了
我们用 \(j\) 来表示当前到了第几位,但是 \(i\) 的话是代表现在的总长
注意这两个的区别,\(i\) 是代表当前匹配的 \(B\) 串的子串长度,\(j\) 是当前匹配的 \(B\) 串的子串的 前缀 和 后缀 到了第几位
那么操作流程
实际上我们可以完全通过 \(nxt[1]\) \(nxt[2]\) …… \(nxt[i - 1]\),来求出这个 \(nxt[i]\)
咋求呢?
我们可以自我匹配,当这个 \(b[j + 1] == b[i]\),时,说明匹配上了,我们来下一位,即 \(j++\)
那么匹配不上的话,我们就将当前的 \(j\) 给换到前面去,换到第 \(j\) 位最长 前缀 和 后缀 长度,知道能够匹配上为止,即当 \(b[j + 1] != b[i]\) 时,\(j == nxt[j]\)
当然,我们每次算完肯定要记录啊,所以在每次算完后 \(kmp[i] == j\)
然后我们贴贴代码
inline void pre() {
int j = 0;
for (int i = 2; i <= lb; i ++) {//第一位肯定是0,无需匹配
while (j && b[j + 1] != b[i])//匹配不上的时候
j = nxt[j];//就往回搜
if (b[j + 1] == b[i])
j ++;//不然往前搞
nxt[i] = j; //记录
}
}
习惯性手动操作一波
B:ababd
1.j = 0, i = 2
那么b[j + 1] != b[i] 并且 j == 0
所以nxt[i] = nxt[2] = j = 0
2.j = 0, i = 3
那么b[j + 1] == b[i] == 'a'
所以j ++
即nxt[i] = nxt[3] = j = 1
3.j = 1, i = 4
那么b[j + 1] == b[i]
所以 j ++
即nxt[i] = nxt[4] = j = 2
4.j = 2, i = 5
那么 b[j + 1] != b[i] 并且 j != 0
所以j = nxt[j] = nxt[2] = 0
那么这是b[j + 1] != b[i],但是 j == 0
所以nxt[i] = nxt[5] = j = 0
很简单易懂吧
所以我们就解决了 \(kmp\) 算法的一半了
接下来就是正式的 \(kmp\) 了(什么,现在才到kmp,滚)
\(So\),我们还是介绍下算法流程
其实这这不过是换了个东西匹配,吧 \(B\) 串和 \(B\) 串自个儿匹配,变成了 \(A\) 串罢了
所以啊,具体的操作和上面差不多
同样枚举 \(i\),但是这个 \(i\) 是 \(A\) 串子串长度,\(j\) 是当前的 \(B\) 串匹配到了第几位
如果当前这个 \(b[j + 1] == a[i]\),说明匹配上了,往下搞,就是 \(j ++\)
如果不行,就是 \(b[j + 1] != a[i]\),那匹配不上,我们和上面求 \(nxt\) 一样,退到前面,退回第 \(j\) 位最长 前缀 和 后缀 长度,就是 \(j = nxt[j]\)
那么当我们匹配完毕,就是 \(j == lb\) 时,匹配完毕,\(ans ++\)
同样,为了继续匹配,我们每次匹配完毕时,应该吧 \(j\) 调整,就是 \(j == kmp[j]\)
注意,不是 每次操作 完,是 每次匹配完毕
贴下代码
inline void kmp() {
int j = 0;
for (int i = 1; i <= la; i ++) {//这个要从第一个字母匹配
while (j && b[j + 1] != a[i])//不匹配
j = nxt[j];//往回搜
if (b[j + 1] == a[i])
j ++;//不然往前搞
if (j == lb) {//匹配完毕
ans ++;
j = nxt[j];//为下次匹配做好准备
}
}
}
样例懒得模拟了,反正这个就和求 \(nxt\) 差不多
然后推荐例题,有空更新
3.Trie树
关于踹树 \(trie\) 树
\(Trie\) 这东西还是很好学的
我还是先偷一棵 \(Trie\) 树(为什么我每次都要偷树)
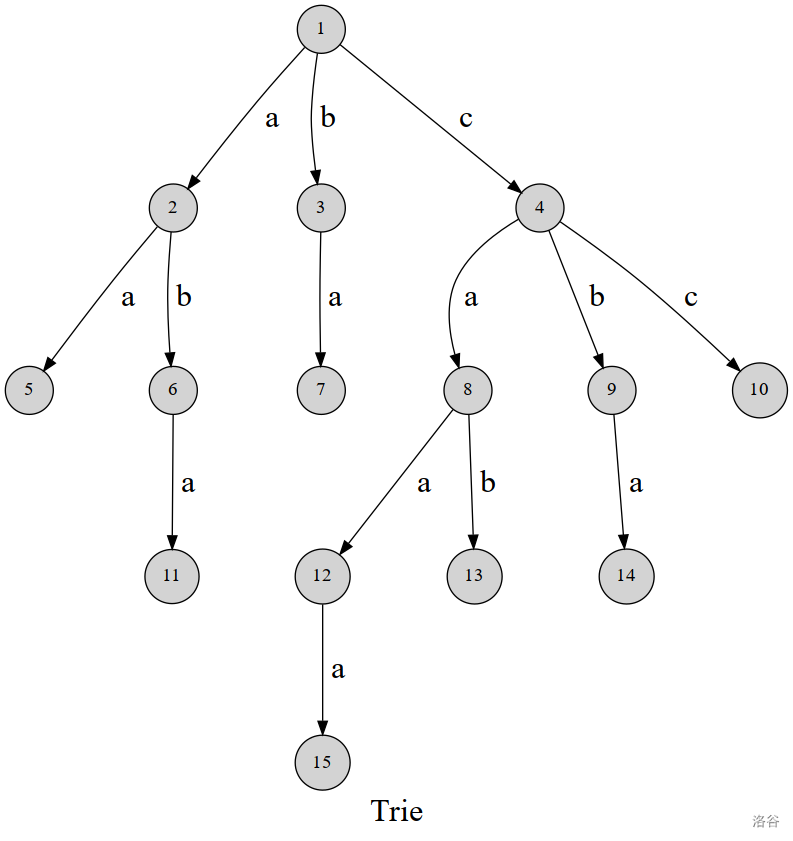
不难得知,我们这个 \(Trie\) 树,就是一个个插入节点,相同的跟着风,不同的自己创
所以,我们自己插入节点也就比较简单的啦
首先要理解几个变量
\(tot:\) 一共有几个节点,本篇代码中根节点为 \(1\)
\(pos:\) 当前遍历到哪个节点了
\(c:\) 当前这个字母的值
\(trie:\) \(trie\) 数组
\(flag:\) 在每个字符串末尾标记用,便于统计
思路很明显,就是在插入时看看当前有没有路可走,没有就自己造一个,有就跟着老路,最后将字符串末尾给标记一下,好统计
下面给出代码
inline void insert(char *ss) {
int len = strlen(ss + 1), pos = 1;
for (int i = 1; i <= len; i ++) {
int c = ss[i] - 'a'
if (! trie[pos][c])
trie[pos][c] = ++ tot;
pos = trie[pos][c];
}
flag[pos] = 1;
}
接下来是查找
这里贴的是判断是否是前缀
所以我们只需要看看当前搜索的子串中被标记的符号有几个,大于 \(1\) 个就说明是前缀,因为自己本身也有一个,所以要大于 \(1\) 个
代码如下
inline bool find(char *ss) {
int len = strlen(ss + 1), pos = 1, cnt = 0;
for (int i = 1; i <= len; i ++) {
int c = ss[i] - '0';
pos = trie[pos][c];
if (flag[pos])
cnt ++;
}
if (cnt > 1)
return 1;
return 0;
}
\(Trie\) 树相比 \(KMP\) 较为简单,所以 \(KMP\) 是讲的比较多的,\(Trie\) 树会偏少
下面是例题,本人懒得写题解了
接下来就是 \(AC\) 自动机了
剧透下,这可以说是 \(KMP + Trie\) 树
4.AC自动机
没错他不能让你直接 \(AC\) 并能让你自动 \(WA\)
好吧我们进入正题
先来一个背景:AC自动机模板(easy)
上面说了
\(AC\) 自动机是 \(KMP + Trie\) 树
所以我们还是要建一个 \(trie\) 树(根节点为 \(1\))
建树的过程不再赘述,代码如下
inline void insert(char *ss) {
int len = strlen(ss + 1), pos = 1;
for (int i = 1; i <= len; i ++) {
int c = ss[i] - 'a';
if (! trie[pos][c])
trie[pos][c] = ++ tot;
pos = trie[pos][c];
}
cnt[pos] ++;
}
现在我们要像 \(KMP\) 一样建一个 \(nxt\) 数组, 但是这次我们不叫 \(nxt\),叫 \(fail\) 了
那么这个家伙的意思就是:如果说从 \(root\) 到 \(i\) 的串我们设为 \(A\),从 \(root\) 到 \(j\) 的串我们称为 \(B\),则 \(B\) 是 \(A\) 的最长后缀
先看看我们的字典树
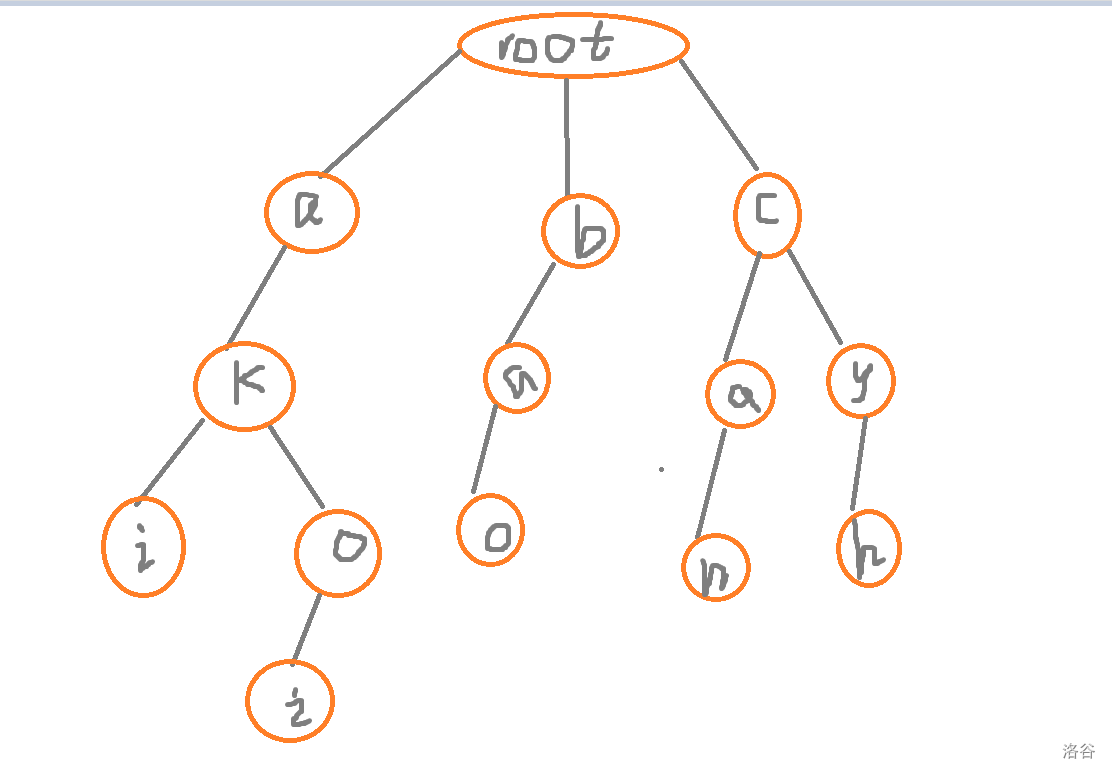
开始找 \(fail\)
很明显,由图可知,根节点所有的孩子的 \(fail\) 边所指向的点都是根节点
那么我们是不是可以这样:
把所有根节点的儿子的 \(fail\) 先预处理出来
然后接下来开始匹配
我们先遍历到这个 \(a\) 的一个儿子即 \(k\)
明显的,他没有一个是能够匹配的上的,于是他的 \(fail\) 边只能指向根节点
\(RT\)
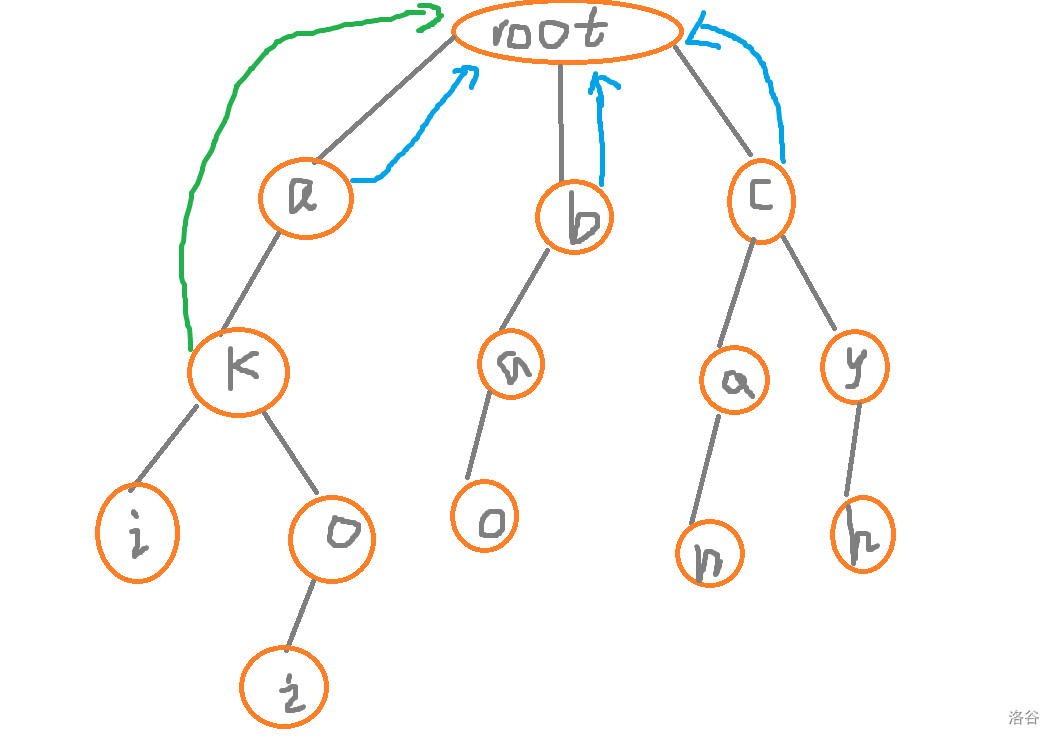
绿色的即为第三层的 \(fail\) 边,第二层的 \(fail\) 边即为蓝色的
接下来我们遍历 \(b\) 的儿子即为 \(a\)
那么明显的有一个 \(a\),所以这个 \(fail\) 边便可以连向 \(a\)
\(RT\)
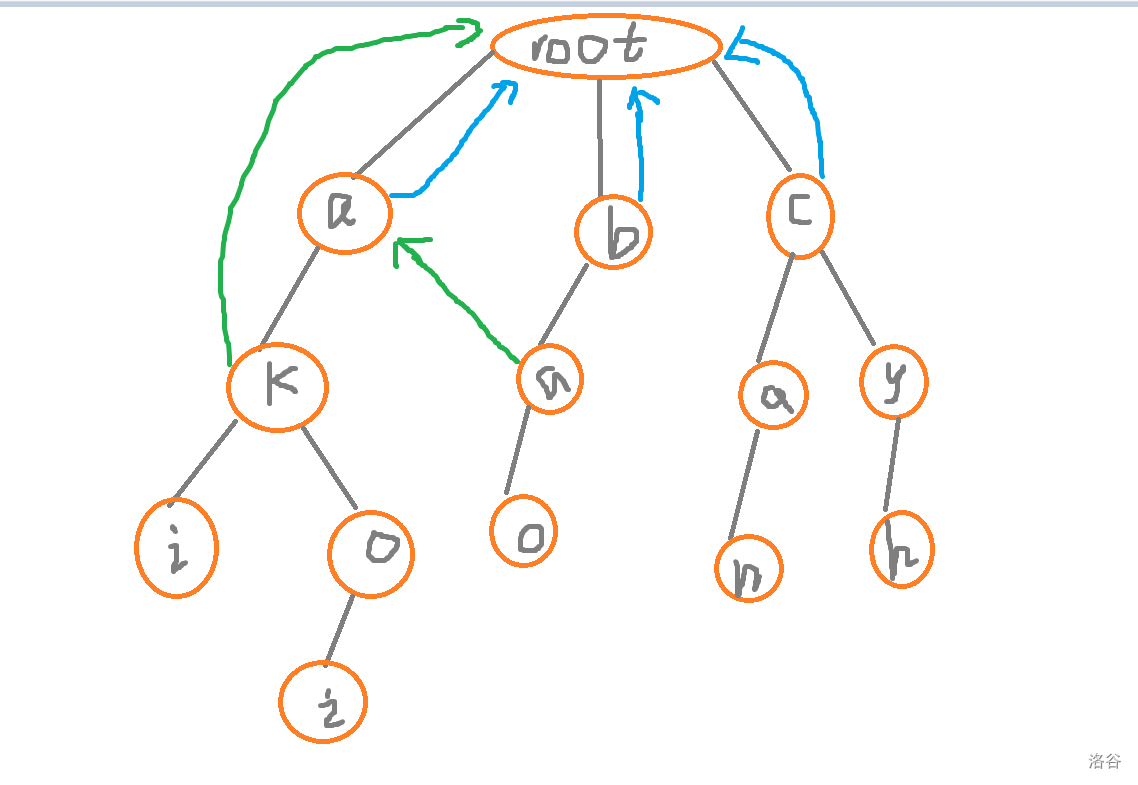
那我们再来遍历 \(c\) 的儿子,即为 \(a\)
那么我们同样的还能找到那个 \(a\)
再来看 \(y\)
没有与之匹配的 \(fail\) 边
便只能连向根节点
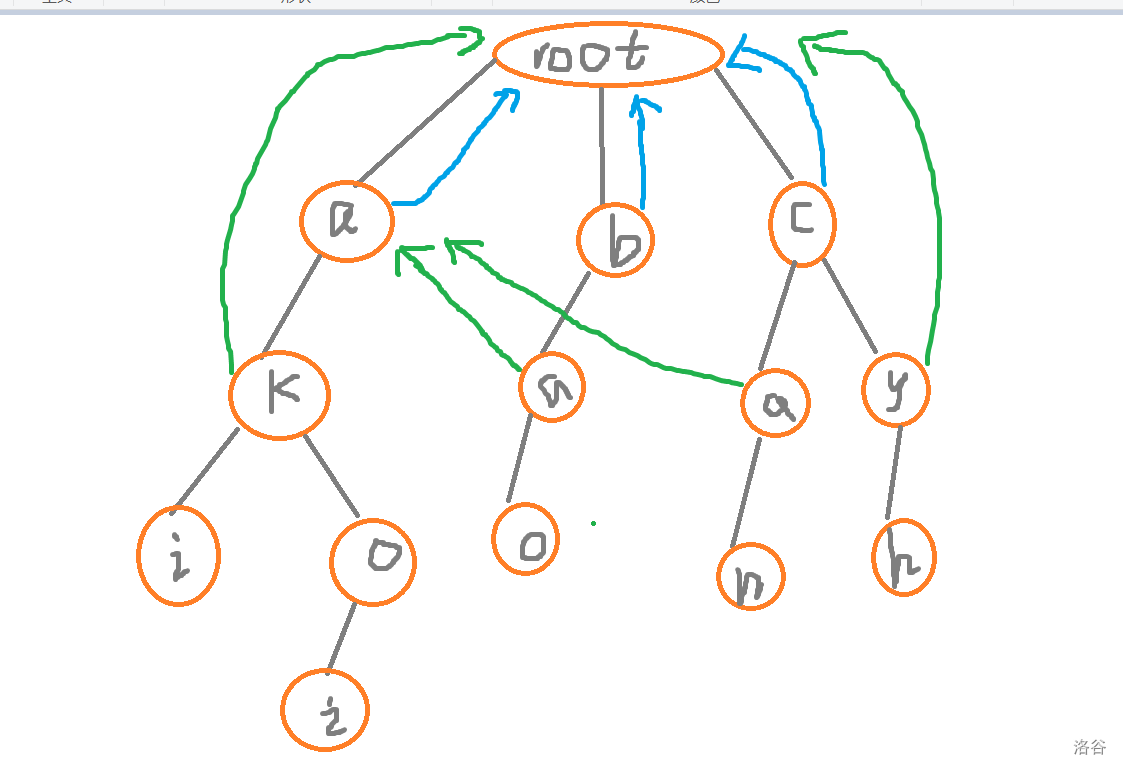
所以然后接下来便可以遍历 \(k\) 的儿子就是 \(i\)
明显,\(i\) 也没有相同的字母, \(fail\) 边还是指向根节点
再来看 \(k\) 的另一个儿子 \(o\),明显的,我们也只能指向根节点
\(RT\)
\(fail\) 边即为紫色边
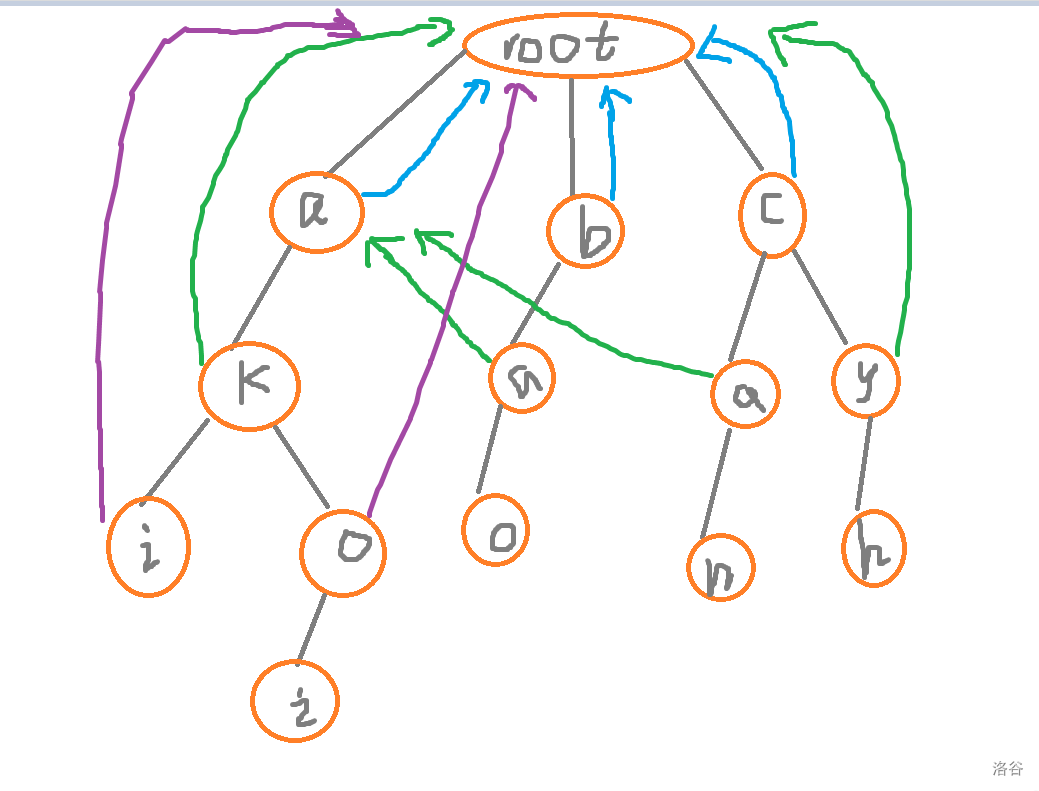
然后我们再来看这个 \(a\) 的儿子,就是 \(o\)
我们从 \(o\) 的爸爸即为 \(a\) 的 \(fail\) 看,其实可以发现是没有的
所以还是连向根节点
那么这到底是什么情况呢?
偶然?
我们看看之前所有连接的
如果我们把 \(pos\) 设为当前要求的 \(fail\) 的点,那么是不是上面所有的点的 \(fail\) 边都可以看成 \(pos\) 他爹的\(fail\) 边有无这个儿子 \(k\)
若有,\(fail\) 边连向 \(k\)
若没有,连向根节点
并且,我刚刚遍历是不是按层遍历,即为 \(bfs\)
所以我们可以用队列实现
一个个儿子遍历过去,碰到的有这个儿子(真儿子),便可查询
但是如果没有呢(假儿子)
好办,把连接假儿子的边设为他父亲这个点的 \(fail\) 边所指向的与其相同字母的儿子
代码就出来了
inline void bfs() {
queue <int> q;
for (int i = 0; i < 26; i ++) {
int pos = trie[1][i];//根节点的儿子(包括真假)
if (pos) {//真儿子
fail[pos] = 1;//fail数组指向根节点
q.push(pos);//入队
}
}//把根节点的儿子设为根节点,方便查询,并把他们入队
while (! q.empty()) {//开始匹配
int u = q.front();//取出队头
q.pop();//弹出
for (int i = 0; i < 26; i ++) {//一个个儿子遍历
int pos = trie[u][i];//u 的为i字母的儿子(包括真假)
if (pos) {//如果u的这个儿子是真儿子
fail[pos] = trie[fail[u]][i];//就把u这个点的儿子的fail边设置为u的fail边的那个同样的儿子
if (! fail[pos])
fail[pos] = 1;
q.push(pos);//入队
} else//如果是假儿子
trie[u][i] = trie[fail[u]][i];// 就把u的连接假儿子的边设为u这个点的fail边所指向的与其相同字母的儿子
}
}
}
接下来是查询
既然是查询哪些在文本中出现且相同的位置不同即可
我们在每次查询前跳到 \(fail\) 边即可
所以查询也是极其简单的
代码
inline int find(char *ss) {
int len = strlen(ss + 1), pos = 1, sum = 0;
for (int i = 1; i <= len; i ++) {
int c = ss[i] - 'a';
int u = trie[pos][c];
while (u&& cnt[u] != -1) {//有这个儿子且没被搜过
sum += cnt[u];//加上答案
cnt[u] = -1;//标记
u = fail[u]; //跳到fail边
}
pos = trie[pos][c];//向下继续搞
}
return sum;
}
完整代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
const int N = 1e6 + 7;
using namespace std;
char s[N];
int n, tot = 1;
struct AC {
int trie[N][27];
int cnt[N];
int fail[N];
inline void insert(char *ss) {
int len = strlen(ss + 1), pos = 1;
for (int i = 1; i <= len; i ++) {
int c = ss[i] - 'a';
if (! trie[pos][c])
trie[pos][c] = ++ tot;
pos = trie[pos][c];
}
cnt[pos] ++;
}//构建trie 树
inline void bfs() {
queue <int> q;
for (int i = 0; i < 26; i ++) {
int pos = trie[1][i];//根节点的儿子(包括真假)
if (pos) {//真儿子
fail[pos] = 1;//fail数组指向根节点
q.push(pos);//入队
}
}//把根节点的儿子设为根节点,方便查询,并把他们入队
while (! q.empty()) {//开始匹配
int u = q.front();//取出队头
q.pop();//弹出
for (int i = 0; i < 26; i ++) {//一个个儿子遍历
int pos = trie[u][i];//u 的为i字母的儿子(包括真假)
if (pos) {//如果u的这个儿子是真儿子
fail[pos] = trie[fail[u]][i];//就把u这个点的儿子的fail边设置为u的fail边的那个同样的儿子
if (! fail[pos])
fail[pos] = 1;
q.push(pos);//入队
} else//如果是假儿子
trie[u][i] = trie[fail[u]][i];// 就把u的连接假儿子的边设为u这个点的fail边所指向的与其相同字母的儿子
}
}
}
inline int find(char *ss) {
int len = strlen(ss + 1), pos = 1, sum = 0;
for (int i = 1; i <= len; i ++) {
int c = ss[i] - 'a';
int u = trie[pos][c];
while (u&& cnt[u] != -1) {//有这个儿子且没被搜过
sum += cnt[u];//加上答案
cnt[u] = -1;//标记
u = fail[u]; //跳到fail边
}
pos = trie[pos][c];//向下继续搞
}
return sum;
}
} ac;
int main() {
freopen(".in", "r", stdin);
freopen(".out", "w", stdout);
cin >> n;
for (int i = 1; i <= n; i ++) {
scanf("%s", s + 1);
ac.insert(s);
}
ac.bfs();
scanf("%s", s + 1);
cout << ac.find(s) << endl;
fclose(stdin);
fclose(stdout);
return 0;
}
所以
我们的 \(AC\) 自动机就结束了
浅谈字符串结束了
除夕夜开始,止于 \(2021.3.6\)
\(Where\) \(are\) \(you\) \(now\)?
\(Atlantic\).
标签:nxt,int,pos,儿子,fail,简单,字符串,节点 From: https://www.cnblogs.com/Kalium/p/17003279.html