高精度算法学习

link: https://oi-wiki.org/math/bignum/

1. 输入输出

#include <bits/stdc++.h>

using namespace std;

const int LEN = 1004;

int a[LEN], b[LEN];

void clear(int a[]) {
  for (int i = 0; i < LEN; i++) {
    a[i] = 0;
  }
}

void read(int a[]) {
  static char s[LEN + 1];
  scanf("%s", s);
  clear(a);
  int len = strlen(s);
  for (int i = 0; i < len; i++) {
    a[len - i - 1] = s[i] - '0';
  }
}

void print(int a[]) {
  int i;
  for (i = LEN; i >= 1; i--) {
    if (a[i] != 0) {
      break;
    }
  }
  for (; i >= 0; i--) {
    putchar(a[i] + '0');
  }
  putchar('\n');
}

int main() {
  read(a);
  print(a);
  return 0;
}

第27行i >= 1是为了保留0。

往函数中传数组的方法无论是func(int a[])还是func(int *a)都会修改原数组，如果想保证数组不变可以写为func(const int a[])（link）。

static此处用作 静态局部变量，其具有以下特点（link）：
• 该变量在全局数据区分配内存；
• 静态局部变量在程序执行到该对象的声明处时被首次初始化，即以后的函数调用不再进行初始化；
• 静态局部变量一般在声明处初始化，如果没有显式初始化，会被程序自动初始化为0；
• 它始终驻留在全局数据区，直到程序运行结束。但其作用域为局部作用域，当定义它的函数或语句块结束时，其作用域随之结束；

数位逆转 的目的是保证低位对齐，方便运算。

把LEN设的 大一点 可以不考虑边界问题。

2. 高精度加法

#include <bits/stdc++.h>

using namespace std;

const int LEN = 1004;

int a[LEN], b[LEN], c[LEN];

void clear(int a[]) {
  for (int i = 0; i < LEN; i++) {
    a[i] = 0;
  }
}

void read(int a[]) {
  static char s[LEN + 1];
  scanf("%s", s);
  clear(a);
  int len = strlen(s);
  for (int i = 0; i < len; i++) {
    a[len - i - 1] = s[i] - '0';
  }
}

void print(int a[]) {
  int i;
  for (i = LEN - 1; i >= 1; i--) {
    if (a[i] != 0) {
      break;
    }
  }
  for (; i >= 0; i--) {
    putchar(a[i] + '0');
  }
  putchar('\n');
}

void add(int a[], int b[], int c[]) {
  clear(c);
  for (int i = 0; i < LEN - 1; i++) {
    c[i] += a[i] + b[i];
    if (c[i] >= 10) {
      c[i + 1] += 1;
      c[i] -= 10;
    }
  }
}

int main() {
  read(a);
  read(b);
  add(a, b, c);
  print(c);
  return 0;
}

注意第40行的i < LEN - 1，因为43行涉及c[i + 1]的操作，而i的最大不能超过len - 1，若让i = len - 1会使c[i + 1]数组越界。

特别注意第41行是+=不是=，不然前面的进位都没了。

3. 高精度减法

#include <bits/stdc++.h>

using namespace std;

const int LEN = 1005;

int a[LEN], b[LEN], c[LEN];

void clear(int a[]) {
  for (int i = 0; i < LEN; i++) {
    a[i] = 0;
  }
}

void read(int a[]) {
  static char s[LEN];
  scanf("%s", s);
  int len = strlen(s);
  clear(a);
  for (int i = 0; i < len; i++) {
    a[len - i - 1] = s[i] - '0';
  }
}

void print(int a[]) {
  int i;
  for (i = LEN - 1; i >= 1; i--) {
    if (a[i] != 0) {
      break;
    }
  }
  for (; i >= 0; i--) {
    putchar(a[i] + '0');
  }
  putchar('\n');
}

void add(int a[], int b[], int c[]) {
  clear(c);
  for (int i = 0; i < LEN - 1; i++) {
    c[i] += a[i] + b[i];
    if (c[i] >= 10) {
      c[i + 1]++;
      c[i] -= 10;
    }
  }
}

void sub(int a[], int b[], int c[]) {
  clear(c);
  for (int i = 0; i < LEN - 1; i++) {
    c[i] += a[i] - b[i];
    if (c[i] < 0) {
      c[i + 1]--;
      c[i] += 10;
    }
  }
}

int main() {
  read(a);
  read(b);
  add(a, b, c);
  print(c);
  sub(a, b, c);
  print(c);
  return 0;
}

原理和注意点同加法，但是不能处理负数差，需要在a < b时把a - b转换为-(b - a)。

4. 高精度乘单精度

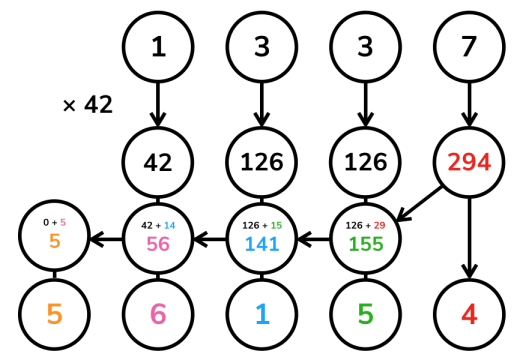
原理不是竖式！

没啥使用价值！

#include <bits/stdc++.h>

using namespace std;

const int LEN = 1005;

int a[LEN], b[LEN], c[LEN];

void clear(int a[]) {
  for (int i = 0; i < LEN; i++) {
    a[i] = 0;
  }
}

void read(int a[]) {
  clear(a);
  static char s[LEN];
  scanf("%s", s);
  int len = strlen(s);
  for (int i = 0; i < len; i++) {
    a[len - i - 1] = s[i] - '0';
  }
}

void print(int a[]) {
  int i;
  for (i = LEN - 1; i >= 1; i--) {
    if (a[i] != 0) {
      break;
    }
  }
  for (; i >= 0; i--) {
    putchar(a[i] + '0');
  }
  putchar('\n');
}

void add(int a[], int b[], int c[]) {
  clear(c);
  for (int i = 0; i < LEN - 1; i++) {
    c[i] += a[i] + b[i];
    if (c[i] >= 10) {
      c[i + 1]++;
      c[i] -= 10;
    }
  }
}

void sub(int a[], int b[], int c[]) {
  clear(c);
  for (int i = 0; i < LEN - 1; i++) {
    c[i] += a[i] - b[i];
    if (c[i] < 0) {
      c[i + 1]--;
      c[i] += 10;
    }
  }
}

void mul_short(int a[], int b, int c[]) {
  clear(c);
  for (int i = 0; i < LEN - 1; i++) {
    c[i] += a[i] * b;
    if (c[i] >= 10) {
      c[i + 1] += c[i] / 10;
      c[i] %= 10;
    }
  }
}

int main() {
  read(a);
  read(b);
  add(a, b, c);
  print(c);
  sub(a, b, c);
  print(c);
  int k;
  scanf("%d", &k);
  mul_short(a, k, c);
  print(c);
  return 0;
}

5. 高精度乘高精度

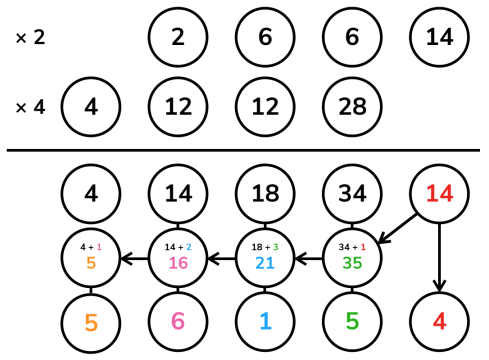
利用乘法竖式原理。

有推论\(c[i] =\sum_{j = 0}^{i}a[j] \times b[i - j]\)（link）。

#include <bits/stdc++.h>

using namespace std;

const int LEN = 1005;

int a[LEN], b[LEN], c[LEN];

void clear(int a[]) {
  for (int i = 0; i < LEN; i++) {
    a[i] = 0;
  }
}

void read(int a[]) {
  clear(a);
  static char s[LEN + 1];
  scanf("%s", s);
  int len = strlen(s);
  for (int i = 0; i < len; i++) {
    a[len - i - 1] = s[i] - '0';
  }
}

void print(int a[]) {
  int i;
  for (i = LEN - 1; i >= 1; i--) {
    if (a[i] != 0) {
      break;
    }
  }
  for (; i >= 0; i--) {
    putchar(a[i] + '0');
  }
  putchar('\n');
}

void add(int a[], int b[], int c[]) {
  clear(c);
  for (int i = 0; i < LEN - 1; i++) {
    c[i] += a[i] + b[i];
    if (c[i] >= 10) {
      c[i + 1]++;
      c[i] -= 10;
    }
  }
}

void sub(int a[], int b[], int c[]) {
  clear(c);
  for (int i = 0; i < LEN - 1; i++) {
    c[i] += a[i] - b[i];
    if (c[i] < 0) {
      c[i + 1]--;
      c[i] += 10;
    }
  }
}

void mul_short(int a[], int b, int c[]) {
  clear(c);
  for (int i = 0; i < LEN - 1; i++) {
    c[i] += a[i] * b;
    if (c[i] >= 10) {
      c[i + 1] += c[i] / 10;
      c[i] %= 10;
    }
  }
}

void mul(int a[], int b[], int c[]) {
  clear(c);
  for (int i = 0; i < LEN - 1; i++) {
    for (int j = 0; j <= i; j++) {
      c[i] += a[j] * b[i - j];
    }
    if (c[i] >= 10) {
      c[i + 1] += c[i] / 10;
      c[i] %= 10;
    }
  }
}

int main() {
  read(a);
  read(b);
  add(a, b, c);
  print(c);
  sub(a, b, c);
  print(c);
  mul(a, b, c);
  print(c);
  return 0;
}

标签：10,高精度,int,void,LEN,学习,++,clear
From： https://www.cnblogs.com/zjsqwq/p/17003137.html

高精度学习