混淆矩阵
(96条消息) 混淆矩阵(Confusion Matrix)分析_vesper305的博客-CSDN博客_confusion_matrix
Confusion Matrix
在机器学习领域,混淆矩阵(confusion matrix),又称为可能性表格或是错误矩阵。它是一种特定的矩阵用来呈现算法性能的可视化效果,通常是监督学习(非监督学习,通常用匹配矩阵:matching matrix)。其每一列代表预测值,每一行代表的是实际的类别。这个名字来源于它可以非常容易的表明多个类别是否有混淆(也就是一个class被预测成另一个class)。
Accuracy - 正确率
Accuracy = (TP + TN) / TotalNum,表示模型分类与标注一致的数量,占总样本的比例
用法:在所有指标中,正确率是最为直观的指标,且普适于多分类。在数据集平衡的场景下,是一个简单好用的指标,尤其对于多分类,是最好用的唯一指标。
缺点:
1)当数据集不平衡时,该指标不能反映模型效果。如99%的样本为负例,此时模型只需要预测所有样本均为负例,即可达到99%的正确率,但显然模型什么也没有学到。
2)作为一个总指标,也不能清晰的看出哪些类别分类不好,为什么没分好。
注意,它和后面要介绍的准确率Precision并不是一个指标,不要混淆。
Precision, Recall, F score - 准确率,召回率,F值
Precision = TP / (TP+FP),即模型认为是正例的样本中,有多少比例是真的正样本。
Recall = TP / (TP + FN),即真实的正例样本中,有多少比例被模型识别出来是正样本了。
F value = 2*Precision*Recall / (Precision+Recall)
F value:
1)目的:P,R 指标虽然较为细粒度的刻画了正例的预测情况,但还缺一个唯一指标来对比优劣。比如A策略相对于B策略,P高,R低,那么到底谁好呢?当然F值只是提供了一种计算方式,它作为唯一指标并不一定合理,要根据场景判断。
2)直观理解:只有P和R都很高时,F值才高。有任何一个指标低,则F值会靠近那个较低的指标。F可以变换为2 / ( 1/P + 1/R )。 从中可以看出,如果P很小,接近于0,则1/P很大,则R是多大已经不重要,最终会约等于P。反之亦然。而当P和R都取到最大值1时,F恰好等于1.
3)F1/F2/F0.5是什么意思:其实我们常说的F值是F1值。F值的原始公式 = (1 + beta^2)*Precision*Recall / (beta^2*Precision+Recall) ,F2即为beta为2时的场景。beta值用于调节Precision和Recall的权重。F0.5更重视precision,而F2更重视recall。详情参考:A Gentle Introduction to the Fbeta-Measure for Machine Learning - Machine Learning Mastery
用途:
1)准召是工业界和学术界最常用的指标。原因是很多情况下,我们只关心正样本而不关心负样本。比如搜索引擎中,我们只关心相关结果(正例)的准召,并不关心不相关结果(负例)的准召,因为虽然后者数量巨大,但后者并不影响用户。
2)而F值则往往使用的更加谨慎,因为我们有时候只关注其中一个指标,比如在搜索场景下,如果正例数量较多,我们只需要一个高准确的分类器即可,而召回可以低一点。虽然有一些其他好结果没有召回,但并不影响用户体验,因为一页只能展示10条结果,用户也不需要把所有的相关结果都看一遍。而在另外一些场景下,则可能需要高召回的分类器而准确率可以适当妥协,例如封禁场景。
3)但如果不使用F值,我们总归缺少一个唯一指标,那么如何对比不同模型的分辨能力呢?其实PR-curve,或Area-Under-PR-curve是一个非常好用的指标,在工业界中尤其是数据集不平衡时,非常好用。比AUC更加好用。后面会介绍。
缺点:当我们关心的是负例而不是正例时,或者不单单是正例时,PR指标会出问题。例如癌症的检测,我们既关心有癌症的病人的准确和召回,也关心没有癌症的病人(负例)被误诊的情况。比如正例明显多于负例的不平衡集合下,一个傻模型把所有来诊断的病人都诊断为癌症,Precision和Recall以及F值都是很高的。但无癌症病人的误诊率也是100%,这是无法接受的。
PR曲线概念:
PR曲线中的P代表的是precision(精准率),R代表的是recall(召回率),其代表的是精准率与召回率的关系,一般情况下,将recall设置为横坐标,precision设置为纵坐标。
AUC与ROC
AUC 是ROC曲线的面积,如下图,绿色曲线是ROC曲线,下面的浅蓝色扇形面积是AUC值。
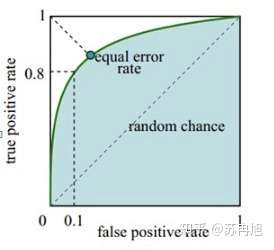
其中ROC曲线:
横轴FPR = FP / (FP+TN),表示的是 1 - 负例召回率,值越小负例召回越好。
纵轴TPR = TP / (TP+FN),表示正例的召回率,值越大正例召回越好。
怎么理解这张图呢
右上角表示,负例完全不召回的情况下正例完全召回,只要把分类阈值设的足够低,这种情况一定可以发生,因此ROC总能连接右上角;左下角则表示负例完全召回时,正例完全不召回,同样是一定可以发生;而最为重要的左上角,表示负例完全召回的情况下,正例也要完全召回,可以想象一个100%正确率的分类器是可以做到这一点的,此时ROC曲线是一个倒L型直角,积分面积覆盖整个矩形,AUC也是最大的。而非100%正确率的分类器则不可能经过左上角,而会趋向于对角线,正常的分类器曲线则与图中类似。最差的情况下,一个纯随机的分类器ROC曲线就是对角线,此时AUC是0.5。
AUC的缺点也很明显,无法应对多分类,尤其是当我们只关心正样本时(即我们只关心正例的准确和召回,并不关心负例的召回),AUC的高低和实际用户感受就不一样了。
AUPR与PR曲线
AUPR在实践中非常好用,只要你不关心负例,它可以无视任何程度数据集倾斜的影响
PR曲线中的P代表的是precision(精准率),R代表的是recall(召回率),其代表的是精准率与召回率的关系,一般情况下,将recall设置为横坐标,precision设置为纵坐标。
图我就复用上面的图了,只是此时横轴是 1-召回率,纵轴是准确率,左上角表示准确率100% 且 召回率100%。大家通过意念修改一下 :)