\(AcWing\) \(248\). 窗内的星星
一、题目描述
在一个天空中有很多星星(看作平面直角坐标系),已知每颗星星的坐标和亮度(都是整数)。
求用宽为 \(W\)、高为 \(H\) 的矩形窗口(\(W,H\) 为正整数) 能圈住的星星的亮度总和最大是多少。(矩形边界上的星星不算)
输入格式
输入包含多组测试用例。
每个用例的第一行包含 \(3\) 个整数:\(n,W,H\),表示星星的数量,矩形窗口的宽和高。
然后是 \(n\) 行,每行有 \(3\) 个整数:\(x,y,c,\) 表示每个星星的位置 \((x,y)\) 和亮度。
没有两颗星星在同一点上。
输出格式
每个测试用例输出一个亮度总和最大值。
每个结果占一行。
数据范围
\(1≤n≤10000,\\
1≤W,H≤1000000,\\
0≤x,y<2^{31}\)
输入样例:
3 5 4
1 2 3
2 3 2
6 3 1
3 5 4
1 2 3
2 3 2
5 3 1
输出样例:
5
6
二、解题思路
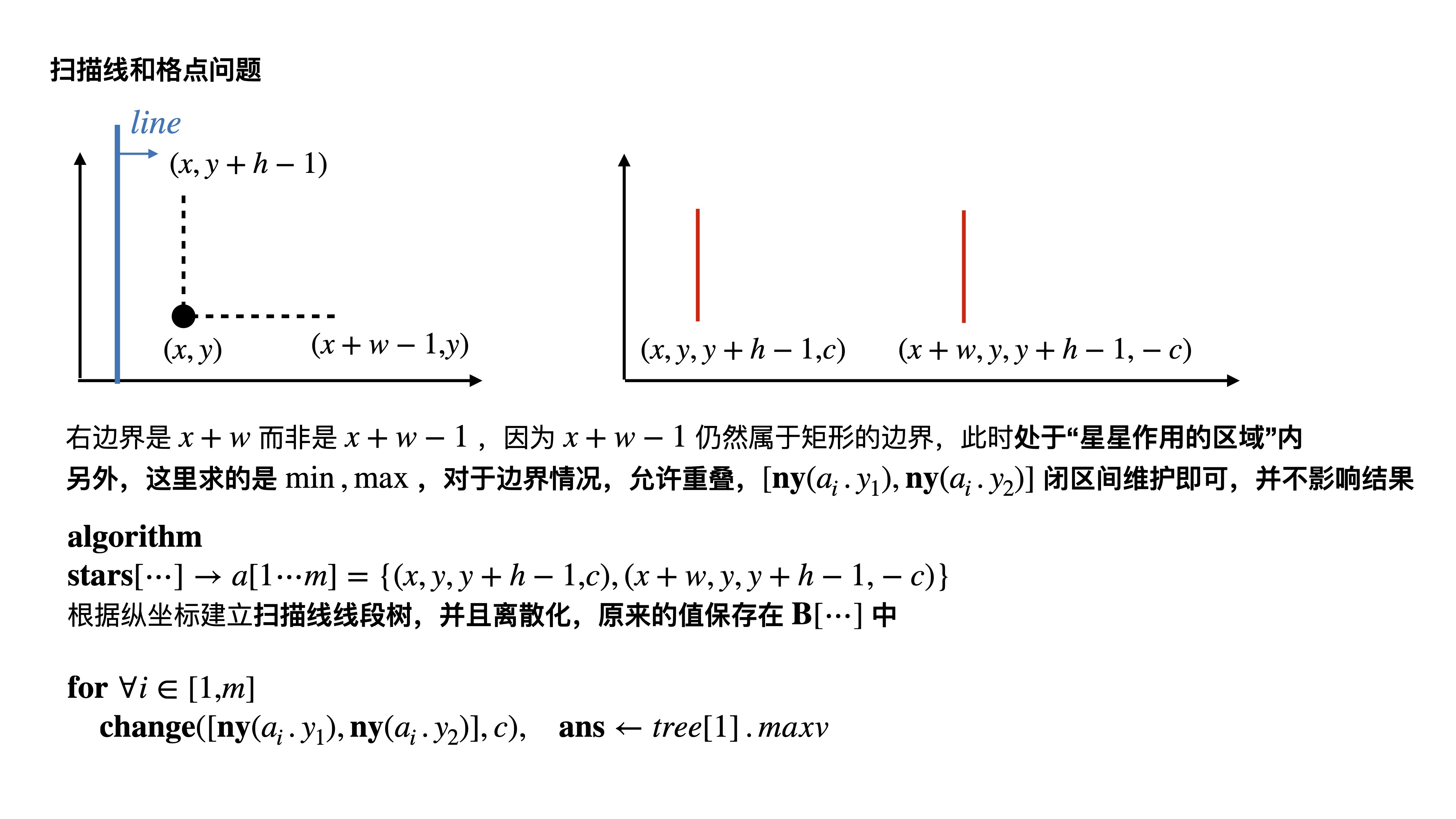
矩形只有中心在一定的范围才能括住特定的星星,假设只有两个星星,括住这两个星星的矩形范围的重叠部分,就是矩形的最佳位置,即能括住最多的亮度的星星
每个星星都有一个矩形,以星星为矩形的左下角(实际上,星星应该在矩形的中心,但坐标平移即可,不影响结果)
把每个矩形的左右两个边, 按照\(x\)升序排列,当\(x\)相同时,星星亮度小的优先
\(Q\):为什么相同\(x\)坐标的边要按照星星亮度再排序一次?
因为题目要求的不包含边界,则达到一个新\(x\)坐标时,应该 先 把负权减掉
\(c\)为星星的亮度,矩形左边赋值\(c\), 右边赋值\(-c\),枚举每个横坐标,线段树中维护着最大的亮度,即是答案
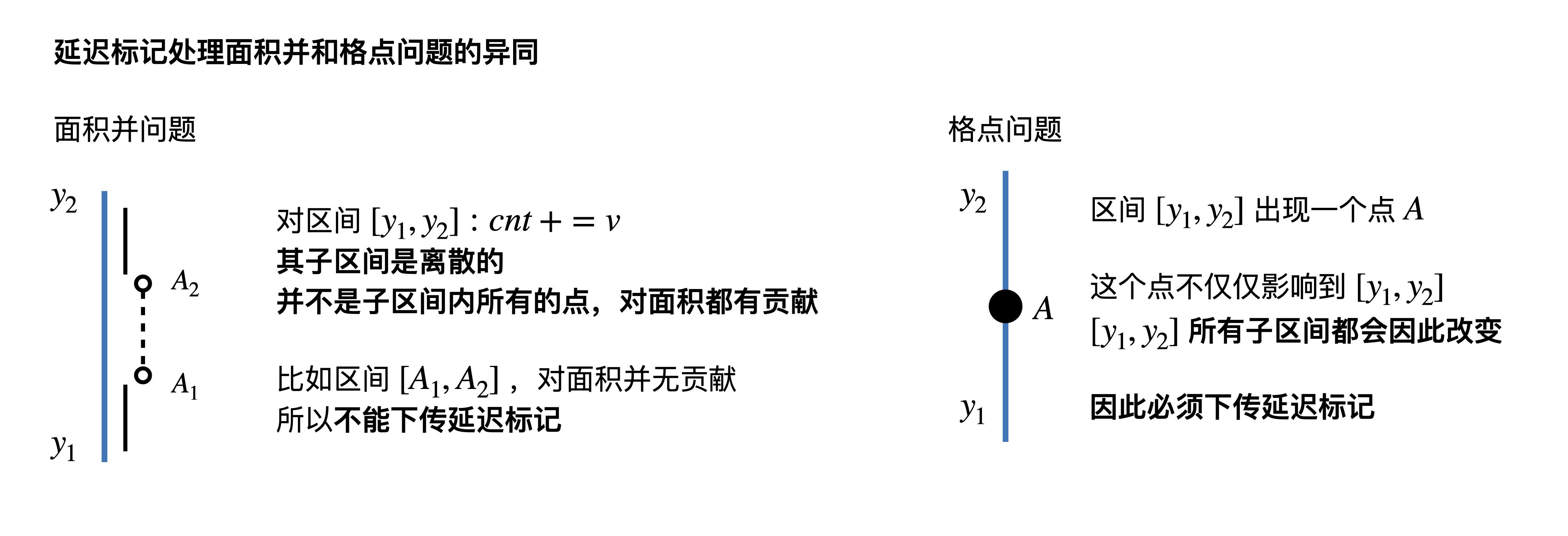
注意这题需要知道最大值的大小,所以 需要懒标记,亚特兰蒂斯那题只需要知道大于\(0\)即可,分析可得不需要懒标记
本例注意和 亚特兰蒂斯 那道题目对比
三、问题集
请问一下 样例中第二个答案是\(6\)也就是三个星星都能框进去 而数据是这样的:
3 5 4
1 2 3
2 3 2
5 3 1
最左边的点是(\(1,2\))最右边的点是(\(5,3\))
那么想要把这两个同时框进去不是需要至少宽度是\(6\)嘛也就是从\(0\)框到\(6\)
可样例中宽度是\(5\) 那么应该会有一个点卡在边界上那么不就不能算是有贡献了嘛?
\(yxc\)回复:
从\(0.5\)到\(5.5\)的框就可以啦,所以宽度是\(5\)的话可以同时包含\((1, 2)\)和\((5, 3)\)
它只是要求星星在整点上,但是我框的矩形顶点是不用在整点上的,所以我们可以平移\(0.5\)这样就能多框一段了。

四、实现代码
#include <iostream>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <vector>
using namespace std;
typedef long long LL;
const int N = 10010;
struct Seg {
LL x, y1, y2, k;
bool operator<(const Seg &l) const {
return x < l.x || x == l.x && k > l.k;
}
} seg[N << 1];
struct Node {
int l, r;
LL maxc, lazy;
} tr[N << 3];
int n, w, h;
vector<LL> ys;
void pushup(int u) {
tr[u].maxc = max(tr[u << 1].maxc, tr[u << 1 | 1].maxc);
}
void build(int u, int l, int r) {
tr[u] = {l, r};
if (l == r) return;
int mid = l + r >> 1;
build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
}
void pushdown(int u) {
if (tr[u].lazy) {
tr[u << 1].maxc += tr[u].lazy;
tr[u << 1].lazy += tr[u].lazy;
tr[u << 1 | 1].maxc += tr[u].lazy;
tr[u << 1 | 1].lazy += tr[u].lazy;
tr[u].lazy = 0;
}
}
void modify(int u, int l, int r, int k) {
if (l <= tr[u].l && tr[u].r <= r) {
tr[u].lazy += k;
tr[u].maxc += k;
return;
}
pushdown(u);
int mid = tr[u].l + tr[u].r >> 1;
if (l <= mid) modify(u << 1, l, r, k);
if (r > mid) modify(u << 1 | 1, l, r, k);
pushup(u);
}
int find(LL x) {
return lower_bound(ys.begin(), ys.end(), x) - ys.begin();
}
int main() {
//加快读入
ios::sync_with_stdio(false), cin.tie(0);
while (cin >> n >> w >> h) {
ys.clear();
for (int i = 1; i <= n; i++) {
LL x, y, c;
cin >> x >> y >> c;
seg[2 * i - 1] = {x, y, y + h - 1, c};
seg[2 * i] = {x + w - 1, y, y + h - 1, -c};
ys.push_back(y), ys.push_back(y + h - 1);
}
sort(ys.begin(), ys.end());
ys.erase(unique(ys.begin(), ys.end()), ys.end());
sort(seg + 1, seg + 1 + 2 * n);
build(1, 0, ys.size() - 1);
LL res = 0;
for (int i = 1; i <= 2 * n; i++) {
modify(1, find(seg[i].y1), find(seg[i].y2), seg[i].k);
res = max(res, tr[1].maxc);
}
printf("%d\n", res);
}
return 0;
}