题目描述
题意:平面上有红色点和蓝色点各 \(n\) 个,且这 \(2n\) 个点没有三个点共线。我们称一种红蓝点之间的配对方案合法,是指在每对点之间用线段连接后,得到的 \(n\) 条线段没有交点。求证:一定存在一种合法的配对方案。
提示:设 \(U=\{1,2,\cdots,n\}\),红色点分别为 \(p_1,p_2,\dots,p_n\),蓝色点分别为 \(q_1,q_2,\dots,q_n\)。一种配对方案是指 \(U\to U\) 的一个双射 \(f\)。一种配对方案合法当且仅当线段集合 \(\{(p_k,q_{f(k)}):k\in U\}\) 中任意两条线段均不相交。
举个例子,当 \(n=3\) 时,下图为一种合法的配对方案,
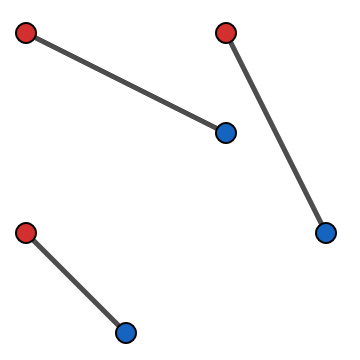
而下图为一种不合法的配对方案,
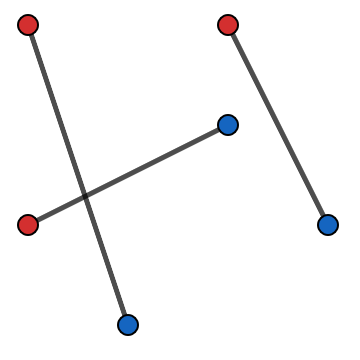
解答
\(n=1\) 的情况是平凡的,下面均假设 \(n\geq2\)。
(反证法)假设不存在一种合法的配对方案。从全部配对方案中选出连接的线段长度之和最短的一种方案,根据反证假设一定存在两条线段相交,设相交的两条线段的红色端点分别为点 \(A\) 和点 \(B\),蓝色端点分别为点 \(C\) 和点 \(D\),\(A\) 和 \(C\) 配对,\(B\) 和 \(D\) 配对,\(AC\) 和 \(BD\) 的交点为 \(E\)。
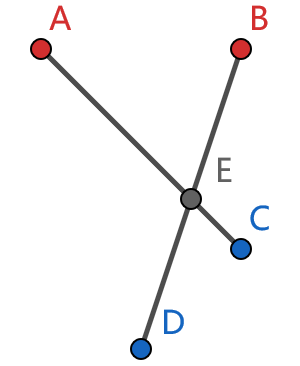
根据三角形不等式,一定有
\[\begin{aligned}|AD|&\leq|AE|+|DE|\\|BC|&\leq|BE|+|EC|\end{aligned} \]由于没有三点共线,等号一定不成立,这说明
\[|AD|+|BC|<|AC|+|BD| \]那么 \(A\) 和 \(D\)、\(B\) 和 \(C\) 配对的方案一定比这种方案线段长度之和更短,矛盾,故假设不成立。于是合法方案一定存在。
2022年12月16日 于东莞松山湖
标签:方案,组合,杂题,线段,选讲,合法,假设,一种,配对 From: https://www.cnblogs.com/szdytom/p/combinatorial-misc-5.html