Unsupervised Sentence Representation via Contrastive Learning with Mixing Negatives
论文地址:https://www.aaai.org/AAAI22Papers/AAAI-8081.ZhangY.pdf
代码地址:https://github.com/BDBC-KG-NLP/MixCSE_AAAI2022
动机:困难样本挖掘对训练过程中维持强梯度信号是至关重要的,同时,随机采样负样本对于句子表示是无效的。
为什么直接用预训练的bert得到的句向量不好?
因为各向异性。各向异性是指嵌入在向量空间中占据一个狭窄的圆锥体。各向异性就有个问题,那就是最后学到的向量都挤在一起,彼此之间计算余弦相似度都很高,并不是一个很好的表示。一个好的向量表示应该同时满足Alignment 和 uniformity,前者表示相似的向量距离应该相近,后者就表示向量在空间上应该尽量均匀,最好是各向同性的[1]。因此,才会有一系列的论文旨在解决各向异性,比如bert-flow、bert-whitening。
对比学习在句子表示中的使用?
对比学习就是我们要学习到一个映射,当句子通过这个映射之后,比如x,我们希望和x相似的正样本的之间的分数要大于和x不相似的负样本的分数,当然,这个分数我们可以自定义一个计算方式。问题是对于大量的数据而言,我们怎么去构建正样本和负样本? ConsBERT使用大量的数据增强策略,比如token shuffling和cutoff。Kim, Yoo, and Lee利用bert的隐含层表示和最后的句嵌入构建正样本对。SimCSE 使用不同的dropout mask将相同的句子传递给预训练模型两次,以构建正样本对。目前的一些模型主要关注的是在生成正样本对时使用数据增强策略,而在生成负样本对时使用随机采样策略。在计算机视觉中,困难样本对于对比学习是至关重要的,而在无监督对比学习中还没有被探索。
对比学习的基本介绍?
我们先定义一个anchor(锚,可以是任意一个句子) \(h_{i}\),定义\((h_{i}, h_{i}^{'})\)是一个正样本对,N个负样本是随机采样得到,\((h_{i},h_{j}^{'})\)表示一个负样本对,那么我们就有最小化以下的对比损失:
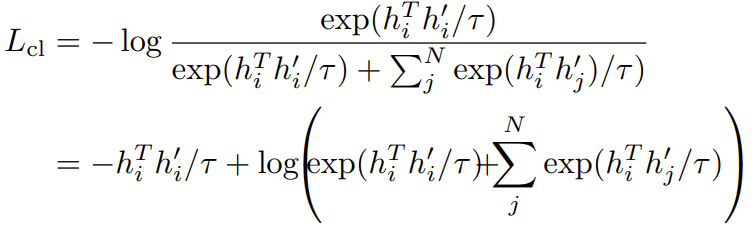
其中\(\tau\)是一个标量温度超参数。以上损失对\(h_{i}\)求偏导可以得到:
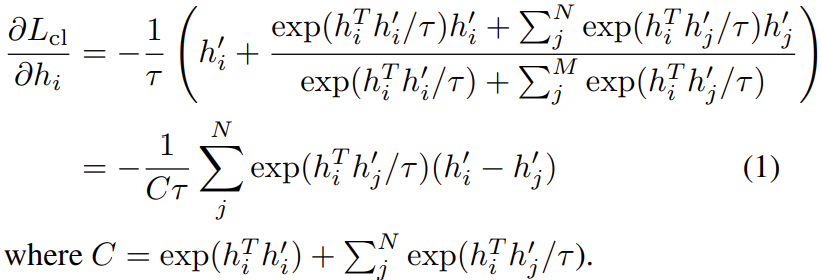
对于每一个负样本特征\(h_{j}^{'}\),\(h_{i}\)沿着\(h_{i}^{'}-h_{j}^{'}\)的方向进行更新。由于\(h_{i}^{'}-h_{j}^{'}=(h_{i}^{'}-h_{i})-(h_{j}^{'}-h_{i})\),这可以视为更新是沿着\(h_{i}^{'}-h_{i}\)的方向,而与\(h_{j}^{'}-h_{i}\)方向相反。换句话说,我们会让正样本\(h_{i}^{'}\)更接近于\(h_{i}\),而让负样本\(h_{j}^{'}\)更远离\(h_{i}\)。注意到公式(1)中第j项的梯度是依赖于\(exp(h_{i}^{T}h_{j}^{'}/\tau)\),所以它随内积\(h_{i}^{T}h_{j}^{'}\)呈指数增长。这扩大了和不同负样本\(h_{j}^{'}\)特征相关的梯度值。因此,锚点上不易分辨的负特征\(h_{j}^{'}\)(即那些内积\(h_{i}^{T}h_{j}^{'}\)较大的)接收到更大的梯度信号,从而将它们推离锚点。
另一方面,注意到\(exp(h_{i}^{T}h_{j}^{'}/\tau)\)<<\(exp(h_{i}^{T}h_{i}^{'}/\tau)\),让\(exp(h_{i}^{T}h_{j}^{'}/\tau)\)相对于\(exp(h_{i}^{T}h_{i}^{'}/\tau)\)显得更没有意义 ,特别是随着训练的进行,前者不断减小,后者不断增加直至接近\(e\)。然后公式(1)给出的梯度信号不断减小,使得训练变慢甚至停止。
在这一点上,我们看到锚附近的负特征的存在对于保持强梯度信号是至关重要的。我们将这种难以区分的负面特征称为“困难负面特征”。这项工作的关键发展是不断地在训练过程中注入人工的困难负面特征,因为原本的困难负面特征正在被推开,变得“更容易”。
MixCSE的基本介绍?
该方法在训练过程中不断地注入人工困难负特征,从而在整个训练过程中保持强梯度信号。
对于锚特征\(h_{i}\),通过混合正特征\(h_{i}^{'}\)和随机负特征\(h_{j}^{'}\)构建负特征:
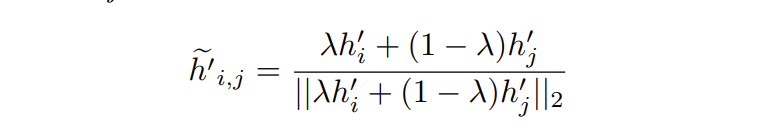
\(\lambda\)是一个超参数,用于控制混合的程度。包含这些混合负特征后,对比损失变为:
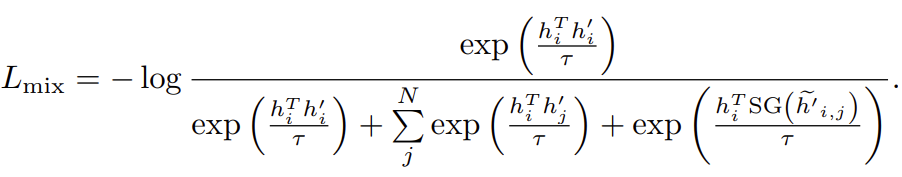
\(SG(.)\)定义为梯度停止,确保在反向传播时不会经过混合负样本。
接着,我们注意到锚和混合负样本的内积:
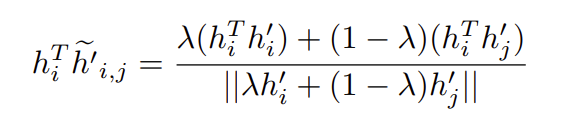
在某些阶段,\(h_{i}^{T}\widetilde{h}_{i,j}^{'}\approx0\)。另外,在实现对齐时,\(h_{i}^{T}h_{i}^{'}\approx1\)。则有:
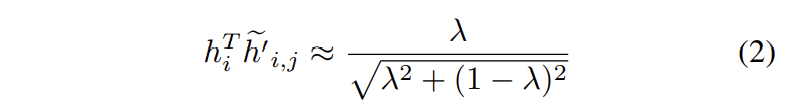
不像标准的负特征\(h_{j}^{i}\)有\(h_{i}^{T}h_{j}^{'}\approx0\)的风险。混合负特征确保内积值始终高于零。这样的负特征则有助于保持更强的梯度信号。
怎么选择\(\lambda\)?
假设有两个正样本特征\(h_{i}^{'}\)和\(h_{i}^{''}\),角度分别为\(0\)和\(\gamma\)。
锚和混合负样本间的角度计算为:
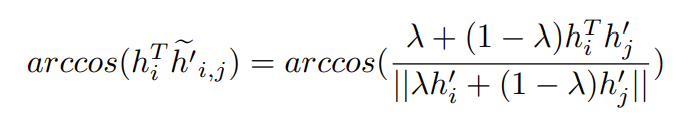
我们既要让混合负样本更接近锚,同时也要让正样本和锚之间比正样本和混合负样本之间更接近,因此\(\lambda\)有一个上界:
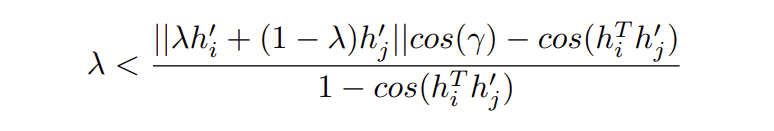
但是我们并不知道\(\gamma\)的值,因此设置较小的\(\lambda\)以避免获得错误的困难样本。
为什么不让混合负样本参与反向传播?
如果参与,计算梯度如下:

我们看到会有一项:
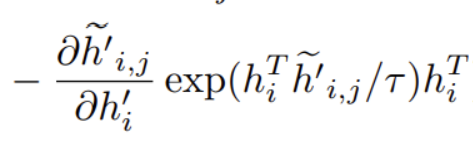
它会使得正样本\(h_{i}^{i}\)逐渐远离\(h_{i}\)。
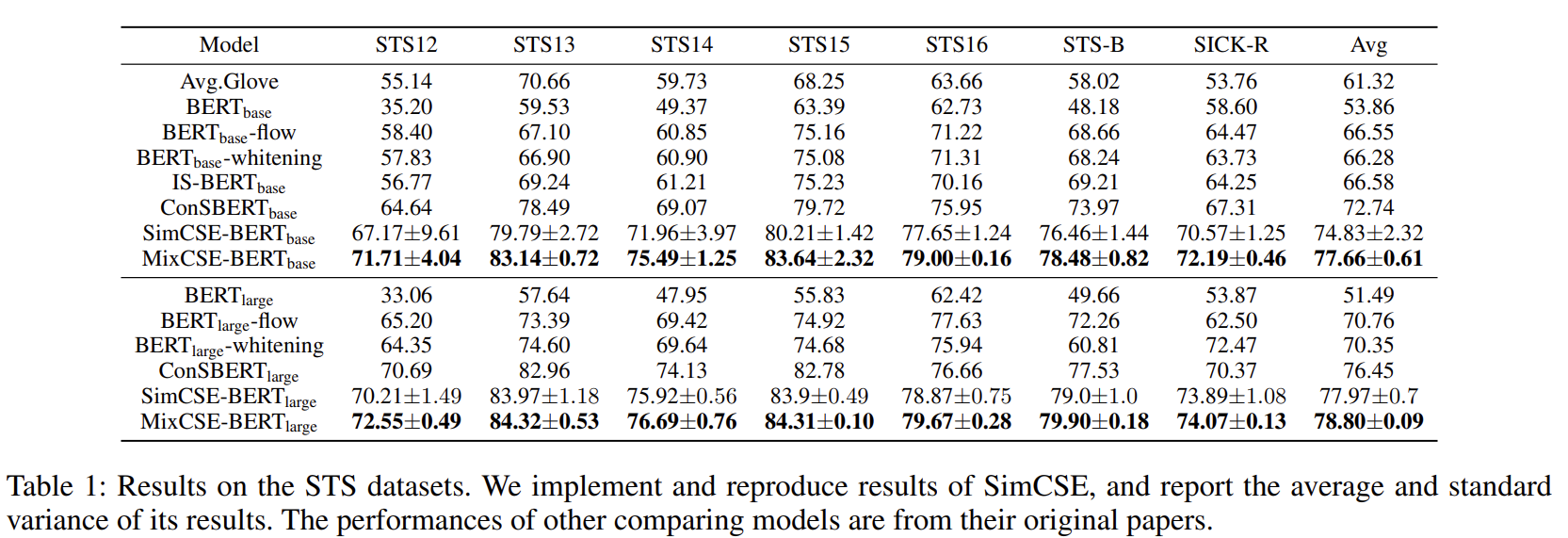
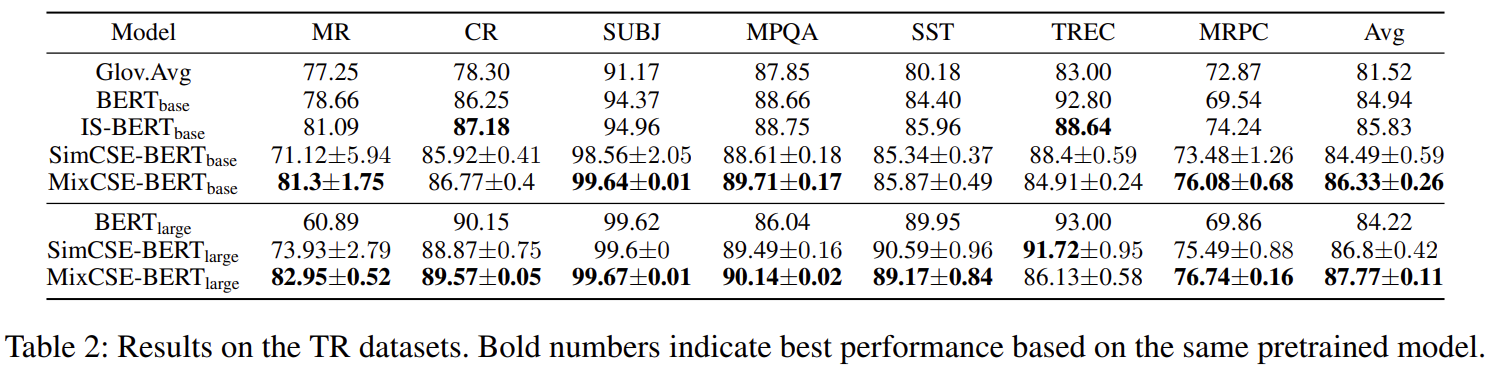
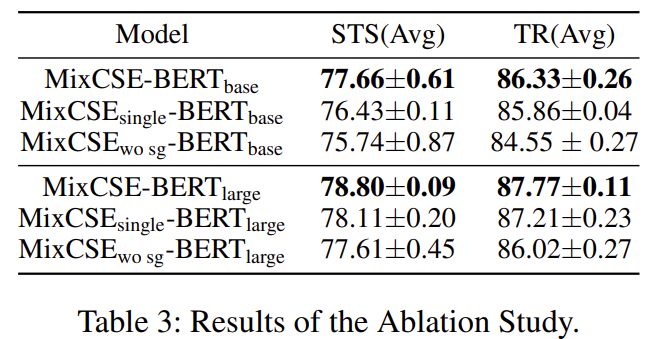
实验结果?