链接:https://www.luogu.com.cn/problem/P6096
题目描述:给定\(n\)条线路,每一条线路可以贯通若干个点,若每座一个地铁就要付\(1\)元。
求:
\(1.\)\(s\)到\(t\)最少要付多少钱。
\(2.\)\(s\)到\(t\)付最小钱的前提下,求最少要坐的站数\(-1\)。
先介绍以下我的\(55\)分做法:
看到第二个问题我们很容易想到最短路图,所以我们考虑第\(1\)问如何建图。
我们可以对每一条铁路中每一个点再多建两个新个节点,可将上面的新节点走一个方向,下面的新节点走一个方向,如下面的方式建图:
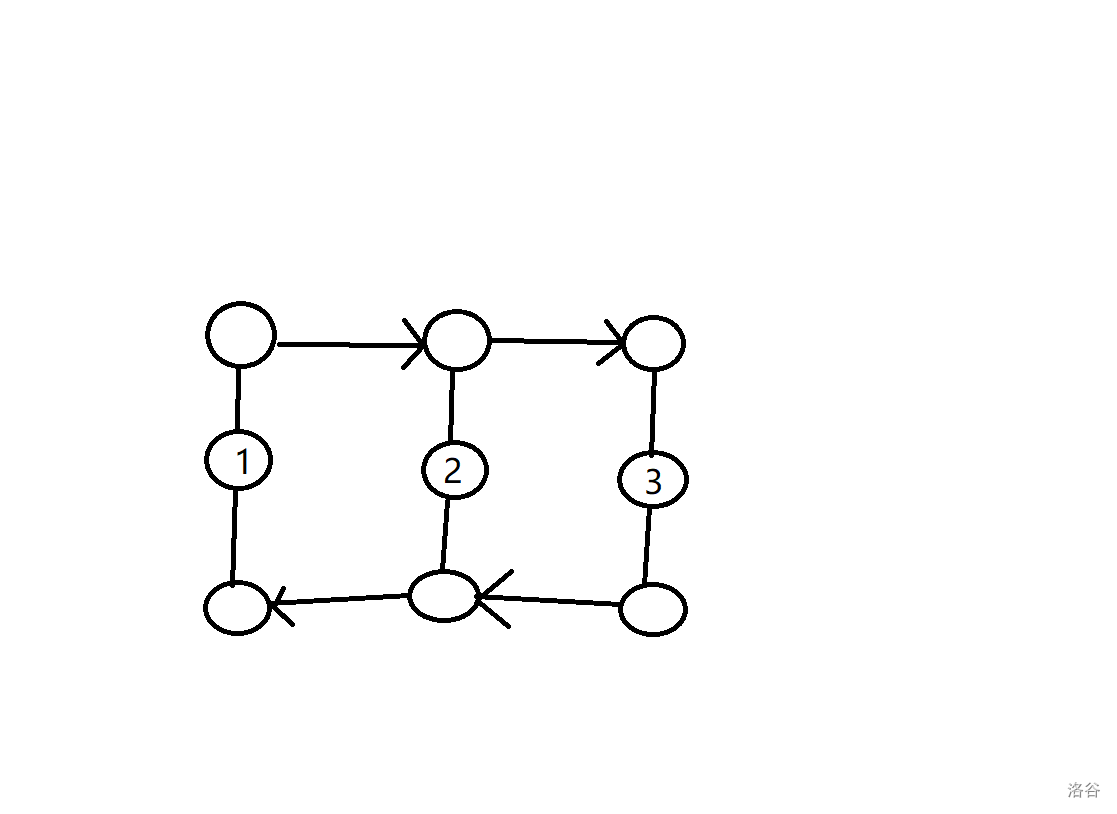
然后跑最短路就可以解决第一问了。
但第二问呢,建出最短路图后要跑最长路,我们只能用\(spfa\),然而我们发现我们建的图其实是网格图,然后\(spfa\)就愉快的被我们自己卡了,于是拿到了\(11\)分。
加上\(SLF+mlcx\)到\(55\)分。
然后这个方法就似乎无法优化下去了。
接下来讲正解:
我们跑第一问的时候对每一个铁路只建一个新的节点就可以了,这个新的节点我们跑最短路时可以可以求出到达它的最短路然后排序,这样就避免了后效性,对于每一条铁路上的点,可以\(dp\)求出满足代价的最长路,具体来说就是在最短路\(dis\)相差一的点转移,因为加入相差一,这个点一定可以走到另一个点,然后这样\(dp\)复杂度就正确了。
#include<iostream>
#include<cstdio>
#include<map>
#include<queue>
#include<vector>
#include<cmath>
#include<algorithm>
using namespace std;
struct node
{
int v,nxt,data,data2;
};
struct reads
{
int num,data;
bool operator < (const reads &a)const
{
return data>a.data;
}
};
reads tmp;
node edge[5000001];
int n,m,head[5000001],s,t,len,dis[5000001],dp[5000001],N;
map<string,int>p;
vector<int>P[5000001];
priority_queue<reads>q;
string k;
bool used[5000001];
inline reads make_reads(register int x,register int y)
{
tmp.num=x;
tmp.data=y;
return tmp;
}
inline void add(register int x,register int y,register int z)
{
edge[++len].v=y;
edge[len].data=z;
edge[len].nxt=head[x];
head[x]=len;
return;
}
inline void dijkstra()
{
register int top;
for (register int i=1;i<=N;++i)
dis[i]=1e9;
dis[s]=0;
q.push(make_reads(s,0));
while (!q.empty())
{
top=q.top().num;
q.pop();
if (used[top])
continue;
used[top]=1;
for (int i=head[top];i>0;i=edge[i].nxt)
if (dis[edge[i].v]>dis[top]+edge[i].data)
{
dis[edge[i].v]=dis[top]+edge[i].data;
q.push(make_reads(edge[i].v,dis[edge[i].v]));
}
}
return;
}
inline int read()
{
register char c=0;
register int sum=0;
while (c<'0'||c>'9')
c=getchar();
while ('0'<=c&&c<='9')
{
sum=sum*10+c-'0';
c=getchar();
}
return sum;
}
inline bool cmp(register int x,register int y)
{
return dis[x]<dis[y];
}
int A[500001];
int main()
{
register int t;
m=read();
n=read();
N=n;
for (register int i=1;i<=n;++i)
{
cin>>k;
p.insert(make_pair(k,i));
}
for (register int i=1;i<=m;++i)
{
t=read();
++N;
for (register int j=0;j<=t-1;++j)
{
cin>>k;
add(p[k],N,1);
add(N,p[k],0);
}
}
cin>>k;
s=p[k];
cin>>k;
t=p[k];
dijkstra();
for (int i=n+1;i<=N;++i)
A[i]=i;
sort(A+n+1,A+N+1,cmp);
register int maxn;
for (register int i=n+1;i<=N;++i)
{
for (register int j=head[A[i]];j>0;j=edge[j].nxt)
P[A[i]].push_back(edge[j].v);
maxn=-1e9;
for (register int j=0;j<P[A[i]].size();++j)
{
if (dis[P[A[i]][j]]==dis[A[i]]-1)
maxn=max(maxn,dp[P[A[i]][j]]-j);
if (dis[P[A[i]][j]]==dis[A[i]])
dp[P[A[i]][j]]=max(dp[P[A[i]][j]],maxn+j);
}
maxn=-1e9;
if (P[A[i]].size()>0)
for (register int j=P[A[i]].size()-1;j>=0;--j)
{
if (dis[P[A[i]][j]]==dis[A[i]]-1)
maxn=max(maxn,dp[P[A[i]][j]]+j);
if (dis[P[A[i]][j]]==dis[A[i]])
dp[P[A[i]][j]]=max(dp[P[A[i]][j]],maxn-j);
}
}
if (dis[t]!=1e9)
printf("%d\n%d\n",dis[t],dp[t]);
else
puts("-1\n0\n");
return 0;
}