J T1 乘方
- \(a=1\),答案为 \(1\)。
- \(a>1\),答案很容易就超过 \(10^9\),直接暴力计算即可。如果在做乘法时进行判断,则可以不开
long long。
J T2 解密
\[p+q=n-e\times d+2 \]\[p\times q=n \]\[p=\frac{y}{q} \]\[\frac{y}{q}+q=n-e\times d+2 \]\[q^2-(n-e\times d+2)\times q+n=0 \]这是一个一元二次方程,二分或者公式求解,两个解即为 \(p\) 和 \(q\)。
J T3 逻辑表达式
输入的字符串是中缀表达式,而「短路」通过后缀表达式能很方便地统计。
一个暴力的想法是模拟这个过程,每次找到当前区间的根结点,然后递归,时间复杂度 \(O(|s|^2)\)。
考虑优化,预处理出每个左括号对应的右括号位置,这样在寻找根结点的过程中遇到被括号包含的区间就可以直接跳过。
容易发现,对于每一种运算符,我们寻找其所有位置所花费时间的总和不会超过 \(O(|s|)\)。因为只有两种运算符,所以总时间复杂度与之相同。
J T4 上升点列
看到单调不降,考虑 DP。答案的形式显然是选择最初的一些点,添加一些点将它们连起来,剩下没用完的点添加到最前面或者最后面。
按 \(x\) 坐标为第一关键字,\(y\) 坐标为第二关键字从小到达排序。令 \(f_{i,j}\) 表示强制选第 \(i\) 个点,前 \(i\) 个点中总共选了 \(j\) 个点,至少需要额外添加的点数。转移直接枚举上一个选的点即可,时间复杂度 \(O(n^3)\)。
利用状态和值对调的套路可以做到 \(O(n^2k)\)。
S T1 假期计划
首先可以 \(O(n(n+m))\) BFS 出任意两点间的最短路。
数据范围只支持我们枚举两个点,观察到 \(A\) 和 \(D\) 的一端均是 \(1\),所以可以对每个 \(B\) 预处理出最优的 \(A\),每个 \(C\) 预处理出最优的 \(D\)。
然后枚举 \(B\) 和 \(C\) 就做完了,注意有不能重复的限制,预处理要保留可能的三个点。
S T2 策略游戏
纯粹的分析题。
先手策略显然是选择最小值最大的那一行,但我们没办法对其直接计算。
关键就在于分析后手的决策,从而得出先手的决策,这样才能够快速找到答案的位置。
- 后手所有数非负或非正,如果先手可选正负性相同的数,就选绝对值最大的,否则就选绝对值最小的。
- 后手可正可负,先手选择非负中绝对值最小的或者非正中绝对值最小的。
S T3 星战
观察到如果满足实现连续穿梭,那么必然满足实现反击,此时图为一棵基环内向树。
也就是每个点出度均为 \(1\),即所有边起点恰好构成了 \(\{1,2,\cdots,n-1,n\}\) 的可重集。
而操作是对于终点的,这意味这我们需要快速处理起点,唯一的方式是利用信息的可合并性。
给每个点随机一个权值,维护所有起点的权值和,如果当前权值和等于所有点的权值和,那么大概率就对了。
对于每个终点,预处理其所有起点的权值和,以及当前其所有不能出发的起点的权值和,这样四个操作都能 \(O(1)\) 解决。
S T4 数据传输
\(k=1\) 是树链求和,树上前缀和或者倍增或者树剖都行。
\(k=2\) 只会用到树链上的点,倍增或者树剖 DP 预处理,最后拆成若干段拼起来,注意在 LCA 处其中一侧要翻转一下。
\(k=3\) 思路一样,但可能会用到与树链相邻的点。具体地,状态有两个参数,记录从链的一端出发向另一端,最多经过几条边能遇到被选择的点。
以下三种情况值得注意
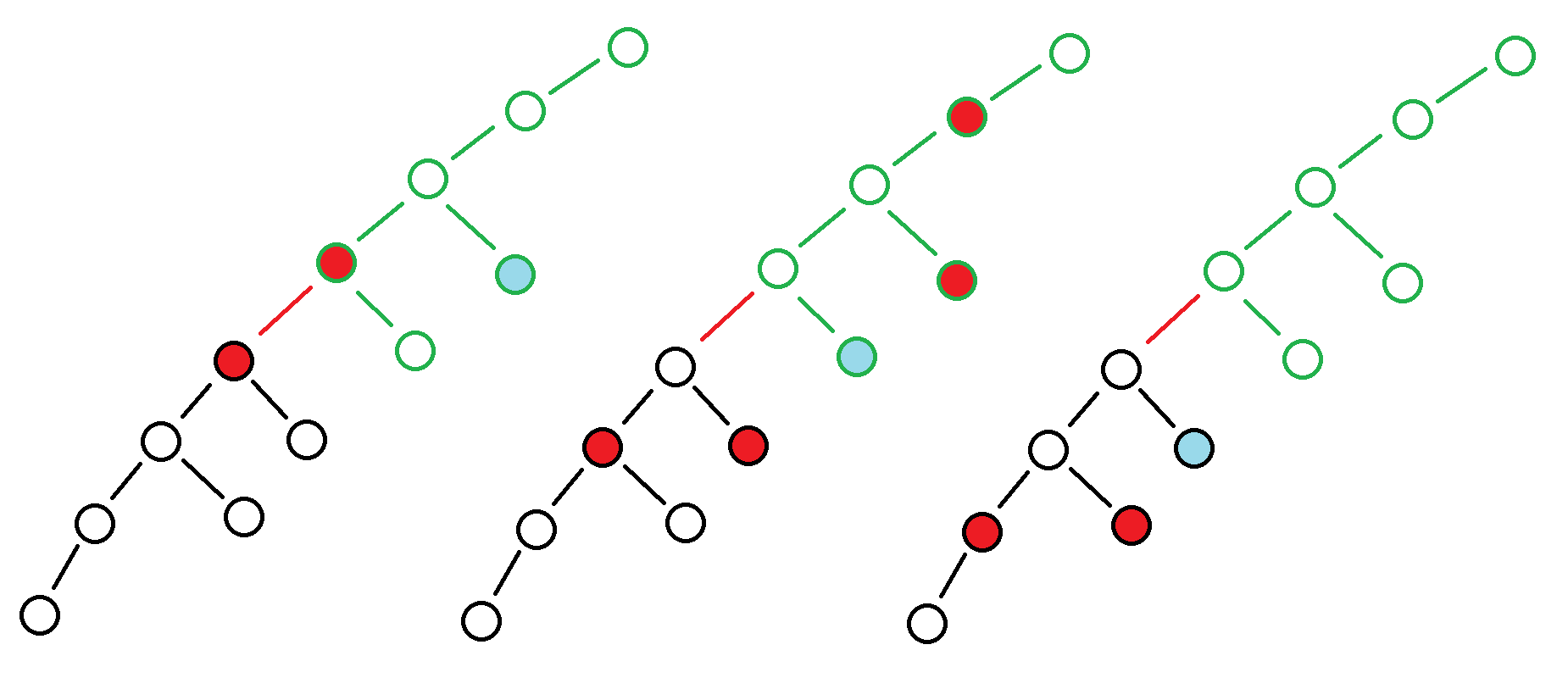
- 第一种是合并时的转移,下方红色点与上方红色点为初始选择,转移时尝试将上方红色点替换成上方蓝色点。
- 第二种也是合并时的转移,下方红色点与上方红色点为初始选择,转移时尝试添加蓝色点。
- 第三种是状态的完善,下方红色点为初始选择,尝试添加蓝色点使得端点距离从 \(2\) 减小到 \(1\)。
处理完这三种情况(其实就对应着距离端点的三种距离),剩余合并就和 \(k=2\) 基本一致了,枚举合法距离暴力转移即可。
细节比较多,但想清楚了也就那么回事,主要还是难在初始状态的处理(包括合并时一侧没有被选择的点)。
标签:报告,CSP2022,times,选择,枚举,解题,权值,添加,预处理 From: https://www.cnblogs.com/shanoamomoprprprprprprprprprprprprprprprprprprprpr/p/16978027.html