leetcode-793. 阶乘函数后 K 个零

793. 阶乘函数后 K 个零

图床：blogimg/刷题记录/leetcode/793/

刷题代码汇总：https://www.cnblogs.com/geaming/p/16428234.html

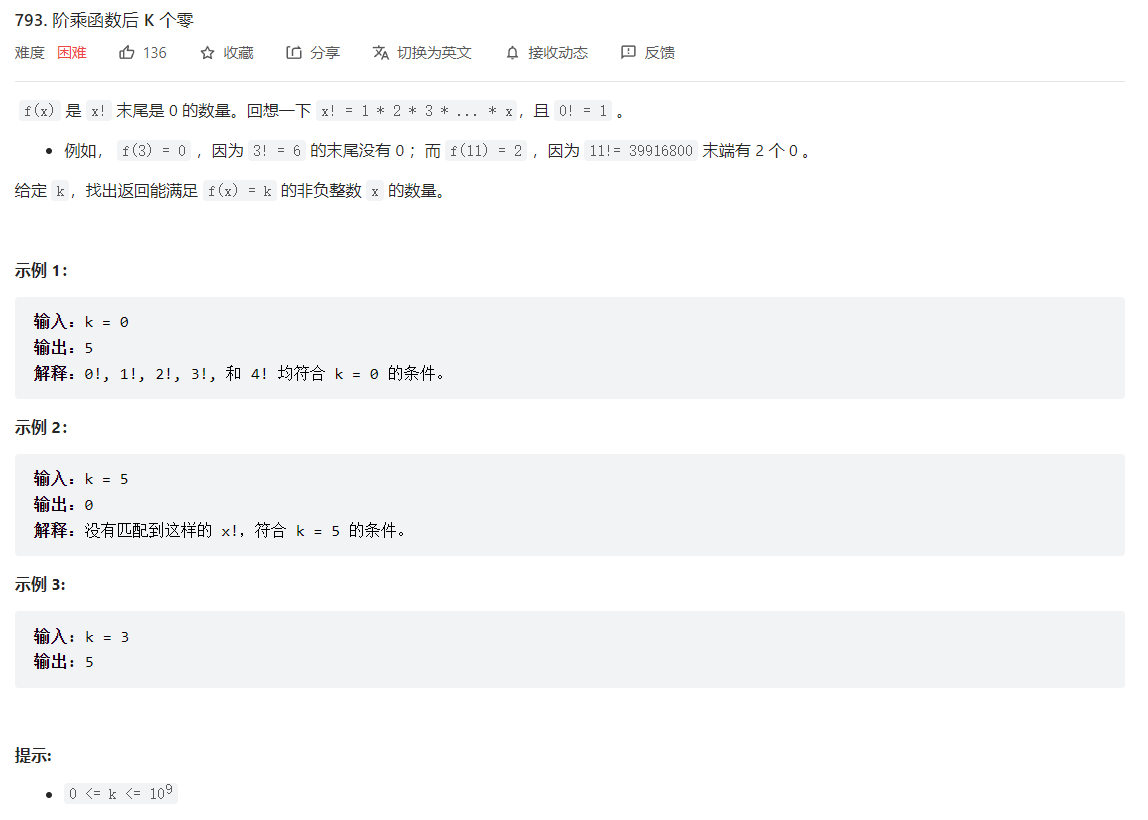
题目

思路

首先我们令\(zeta(x)\)为\(x!\)末尾零的个数。根据172.阶乘后的零有\(zeta(x)=\sum_{k=1}^\infty\left\lfloor\frac{x}{5^k}\right\rfloor\)

记\(n_x\)表示\(x!\)末尾零的个不小于x的最小数，那么题目等价于求解\(n_{k+1}-n_k\)

由于\(zeta(x)\)为单调不减函数，因此\(n_{k+1}\)和\(n_k\)可以通过二分查找来求解。

又因为\(zeta(x)=\sum_{k=1}^\infty\left\lfloor\frac{x}{5^k}\right\rfloor\geq\left\lfloor\frac{x}{5}\right\rfloor\)

得到\(zeta(5x)\geq x\)

所以当二分求解\(n_x\)时，我们可以将二分的初始右边界\(r\)设置为\(5x\)

解法

class Solution {
public:
    int zeta(long x) {
        int res = 0;
        while (x) {
            res += x / 5;
            x /= 5;
        }
        return res;
    }

    long long help(int k) {
        long long r = 5LL * k;
        long long l = 0;
        while (l <= r) {
            long long mid = (l + r) / 2;
            if (zeta(mid) < k) {
                l = mid + 1;
            } else {
                r = mid - 1;
            }
        }
        return r + 1;
    }

    int preimageSizeFZF(int k) {
        return help(k + 1) - help(k);
    }
};

• 时间复杂度：\(O(log^2k)\)，其中\(k\)为题目给定数字，二分查找\(n_{k+1}\)，\(n_k\)的时间复杂度为\(O(logk)\)，其中每一步计算\(zeta(x)\)的时间复杂度为\(O(logk)\)。
• 空间复杂度：\(O(1)\)，\(zeta(x)\)仅使用常量空间

补充