前言
三种最基本的排序方法:选择排序、冒泡排序、插入排序。这些排序并不是学习数据结构时才碰到的,早在学习C++时教材上就有介绍。现在正在学习数据结构,复习并且自己动手实现一下。
本文的代码都是基于数组实现的,以排成升序为例。
选择排序
选择排序的思想:
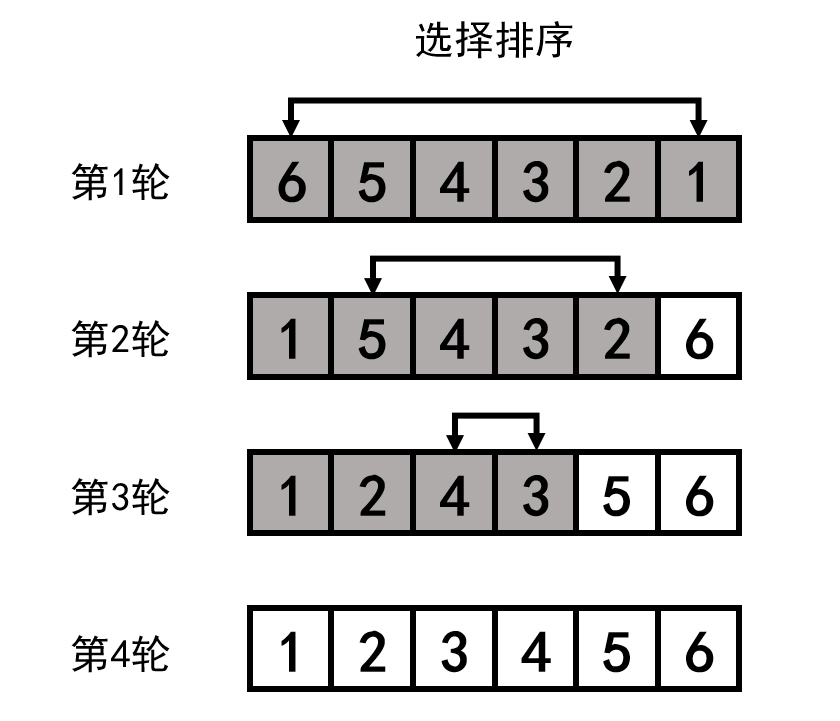
不断选择最大的数依次排到数组最右端,使得数组从右到左逐渐有序。
当然从最小开始也可,本文三种排序默认都是从最大开始。
具体步骤:
- 从头开始遍历数组,找出最大数的下标,将最大数与最右侧的数交换。
- 现在最右侧已经有序,排除最右侧有序部分,重新遍历找出第二大的数,排到右侧第二位。
- 依次类推,重复这一过程,直到数组有序。
这里有一个何时结束程序的问题。很明显,当需要遍历的部分只剩下1个时,表明已经排序完毕了。但有可能出现可以提前结束的情况,某次遍历结束后数组恰好是有序的,就能够提前结束遍历。
因此通常设定一个标志sorted,在每次遍历开始设置为true,即默认已经有序,遍历时一旦出现左>右的情况,就将sorted置为false。
如果这轮遍历没有出现左>右的情况,sorted不会被置false,此时数组已经有序,无需继续下一轮迭代。
可以结合以下示意图理解算法步骤和代码。其中白色表示有序部分,灰色表示无序部分。
完整代码如下,swap函数用于 交换两个位置的数值。
sort.h
/****************************************
* Swap two number.
****************************************/
template<typename T>
void swap(T &x, T &y)
{
T temp = x;
x = y;
y = temp;
}
/****************************************
* Selection-sort in ascending order.
@param
a[]: input array
n: size of input array
****************************************/
template<typename T>
void SelectionSort(T a[], int n)
{
bool sorted = false;
//int iterCount = 0;
for (int size = n; !sorted && size > 1; size--)
{
int indexOfMax = 0;
sorted = true; //每轮遍历前要初始化标志
//寻找最大值的下标
for (int i = 1; i < size; i++)
{
if (a[indexOfMax] < a[i])
indexOfMax = i;
else
sorted = false; //如果有左>右,说明还是无序
}
swap(a[indexOfMax], a[size - 1]); //将最大值与最右端交换
//iterCount++;
}
//std::cout << "iterCount=" << iterCount << std::endl;
}
main.cpp
#include <iostream>
#include <stdlib.h>
#include "sort.h"
template<typename T>
void PrintArray(T arr[], int size)
{
for (int i = 0; i < size; i++)
{
std::cout << arr[i] << '\t';
}
std::cout << std::endl;
}
int main()
{
const int arrSize = 6;
int a1[arrSize] = { 6, 5, 4, 3, 2, 1 }; //for selection-sort
std::cout << "selection-sort:" << std::endl;
PrintArray<int>(a1, arrSize);
SelectionSort<int>(a1, arrSize);
PrintArray<int>(a1, arrSize);
system("pause");
}
将包含iterCount的3行解除注释,分别在最外侧for循环加与不加!sorted条件时测试,会发现确实提前退出了循环。
另外注意两层for循环的边界。外层循环使得无序部分不断缩小(向左缩进),内层循环对目前仍然无序的部分进行遍历,查找最大值。
多说一句
一开始被这种写法困扰了,主要是觉得在判断为无序时给sorted进行了重复的赋值。
然而想要减少重复赋值,目前也只能想到再加一个判断sorted当前值的条件,这样做虽然少了赋值但多了比较,总的来说并没有节约很多操作。
冒泡排序
通常和冒泡排序一起出现的词是“顾名思义”。想象将数组旋转,右端向上,左端向下,冒泡排序每轮迭代让最大值“上浮”到最右端。
冒泡排序的思想:
从左侧开始比较相邻的数,如果左侧值较大,则进行交换,每轮遍历使最大值交换到最右端。
冒泡排序同样有提前结束的优化方法。每当发生相邻交换,就将sorted标志标为false,否则保持这轮循环开始时的true值。如果sorted保持true未变化过,说明本轮已经检测到数组有序。
可以结合示意图理解代码。其中白色表示有序部分,灰色表示无序部分。

完整代码如下:
/****************************************
* Bubble-sort in ascending order.
@param
a[]: input array
n: size of input array
****************************************/
template<typename T>
void BubbleSort(T a[], int n)
{
bool sorted = false;
//int iterCount = 0;
for (int size = n; !sorted && size > 1; size--)
{
sorted = true; //每轮遍历前要初始化标志
for (int i = 1; i < size; i++)
{
if (a[i - 1] > a[i])
{
swap(a[i - 1], a[i]);
sorted = false; //发生相邻交换,目前仍然无序
}
}
//iterCount++;
}
//std::cout << "iterCount=" << iterCount << std::endl;
}
主函数与选择排序类似,这里略去。
用数组{ 6, 1, 2, 5, 3, 4 }测试,可以观察到sorted标志的影响,增加sorted标志后提前退出了循环。
注意两层for循环的边界。外层循环用于缩小无序部分的边界。内层循环用于从左到右遍历比较相邻值,其边界是无序部分的边界。
插入排序
插入排序的思想:
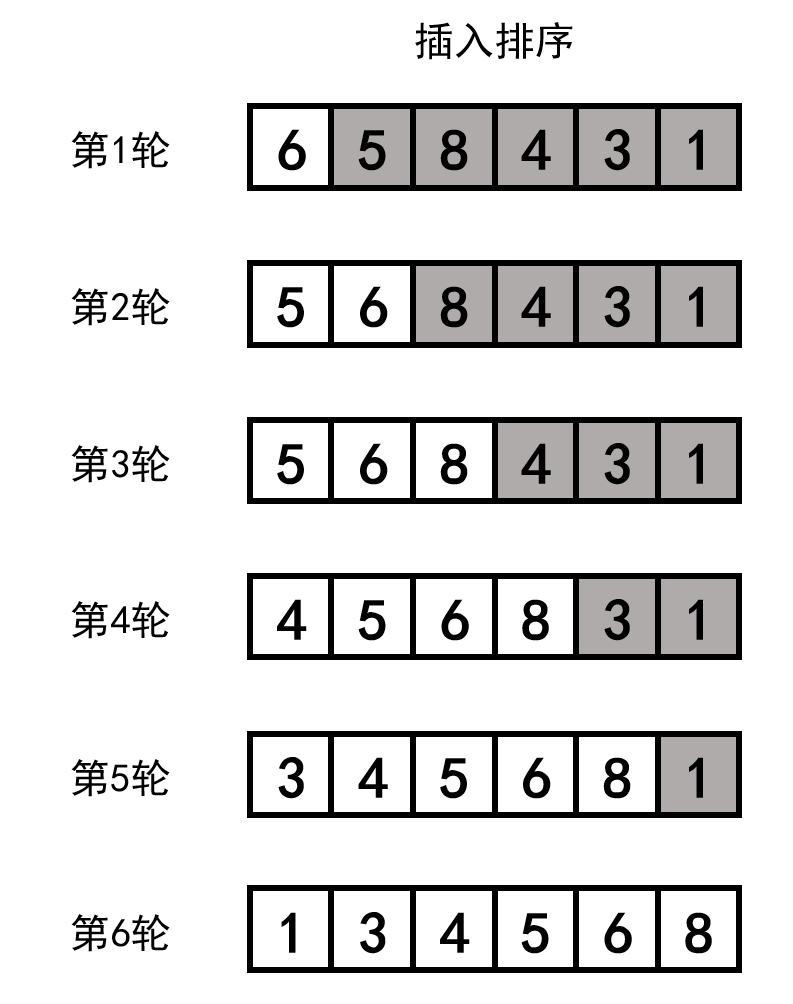
开始时将最左侧a[0]视为有序部分,从a[1]开始,依次将无序部分的数插入到有序部分相应位置。
具体步骤:
选择无序部分第一个数为当前插入数,与左侧有序部分从右向左依次比较,如果插入数较小,则将有序部分被比较的数右移;如果插入数较大,则将插入数插在被比较数的后面。
可以结合示意图理解。其中白色表示有序部分,灰色表示无序部分。
完整代码如下:
/****************************************
* Insertion-sort in ascending order.
@param
a[]: input array
n: size of input array
****************************************/
template<typename T>
void InsertionSort(T a[], int n)
{
//int iterCount = 0;
for (int i = 1; i < n; i++)
{
T numNow = a[i];
int j = i - 1;
for (; j >= 0 && a[j] > numNow; j--)
{
a[j + 1] = a[j];
}
a[j + 1] = numNow;
//iterCount++;
}
//std::cout << "iterCount=" << iterCount << std::endl;
}
主函数与选择排序类似,这里略去。
注意两层for循环的边界。外层循环用于缩小无序边界,与上面两种排序不同,插入排序的无序部分是“向右缩进”的。反过来理解为有序部分由左侧开始“扩张”或许更直观。
而内层循环从有序部分的右边开始,依次寻找插入数的正确位置。当内层循环退出时,下标j已经是比插入数小的数了,应当将后面一个数a[j+1]赋值为插入数。在此之前,更大的数已经安全地移动到了更右侧,无需担心被覆盖。
三种排序方式的比较
特征比较
冒泡排序的特征非常明显:相邻交换,大数上(右)浮。
但选择排序和插入排序的特征好像不是很明显。以前在C++课的时候我一直疑惑,难道选择排序将最大数放到最右端的操作不能理解为一种“插入”吗?只是选择排序是交换,插入排序是依次移动而已。
现在根据我的理解,关键就在于已确定的因素不一样。
选择排序是“定位找数”。每轮迭代前,需要移动的数是未知的,需要去查找。而插入的位置是确定的,即有序部分边缘再向外的一位。
插入排序则是“定数找位”。每轮迭代前,需要移动的数是确定的,即无序部分的第一个数。而插入的位置是未知的,需要依次查找比较。
稳定性比较
选择排序是非稳定排序。在将最大数交换到最右侧时,可能将“不那么小”的数交换到比较靠左的地方,从而可能使无序部分变得“更加”无序。
冒泡排序是稳定排序。总是比较相邻的数,整个数组必然是不断趋向有序的,没有跳过数进行交换,不会将更大的数交换到左侧去。
插入排序也是稳定排序。因为每次移动的数只是无序部分的第一个,之后的数完全不会被影响到。
标签:int,插入排序,无序,冒泡排序,有序,sorted,排序,size From: https://www.cnblogs.com/midoq/p/16961782.html