好题
先手玩一下 \(n=2\) (只有颜色 \(0/1\)) 的情况:

我们假设柱子 \(1\) 上有 \(s\) 个 \(1\),那就先把柱子 \(2\) 顶端的 \(s\) 个球移到 \(3\),变成这样:
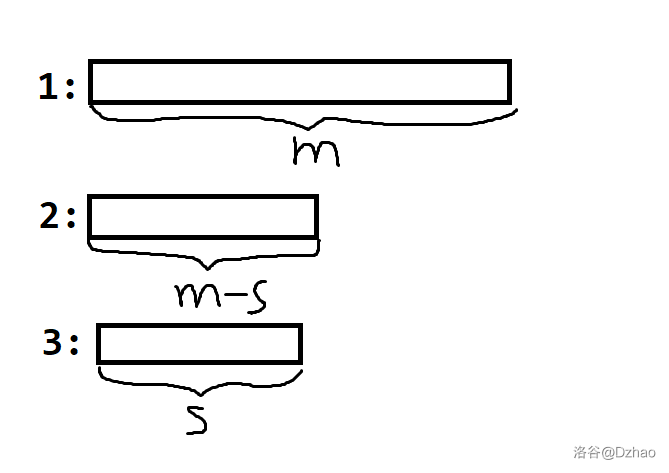
然后把柱子 \(1\) 的所有 \(1\) 移到柱子 \(2\) 上,所有 \(0\) 移到柱子 3上:
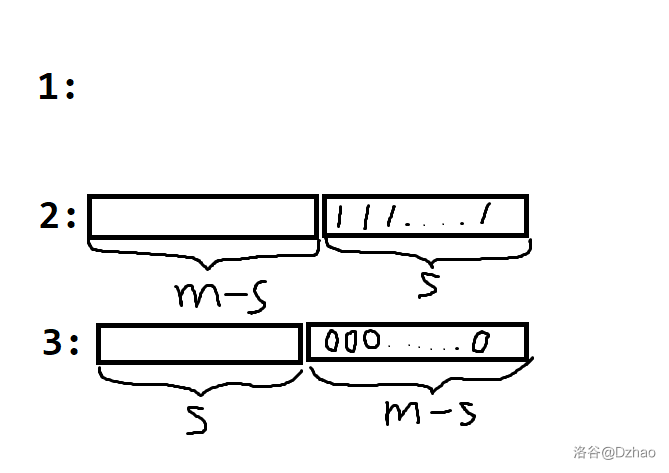
然后再把这些移走的 \(1/0\) 按顺序移回到柱子 \(1\),并把柱子 \(2\) 剩下的 \(m-s\) 个数移到柱子 \(3\) 上:
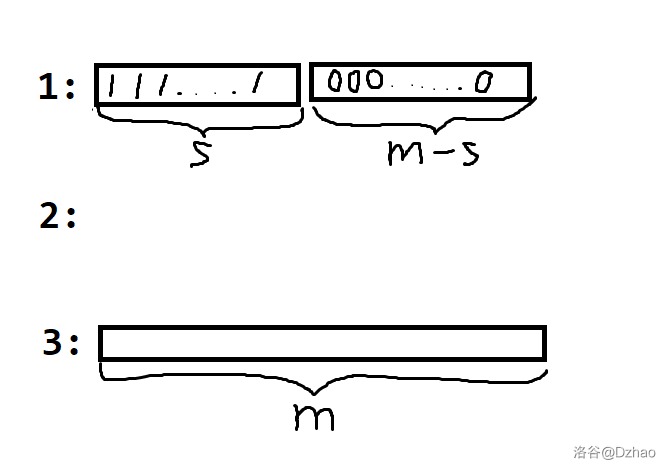
然后把柱子 \(1\) 上的 \(m-s\) 个 \(0\) 移到柱子 \(2\) 上:
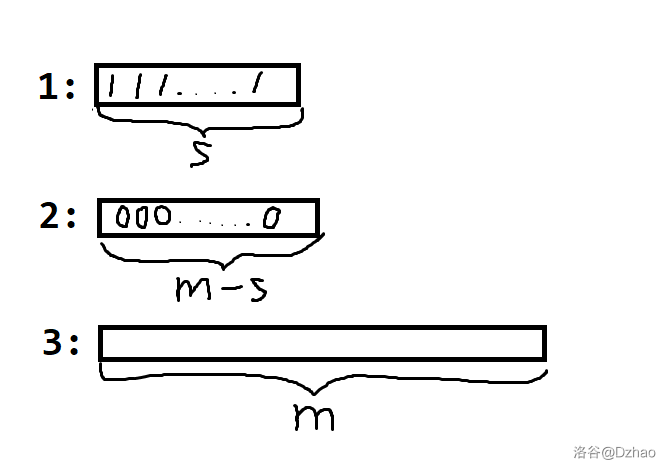
最后再将柱子 \(3\) 所有的 \(1\) 移到柱子 \(1\) 上,所有的 \(0\) 移到柱子 \(2\) 上,那么就移好了:
总操作次数为 \(5m-s\)
考虑能不能把多种颜色的情况转换成很多个两种颜色的问题
可以想到我们设一个值 \(x\) 使 \(\le x\) 的数全部变为 \(1\),\(>x\) 的数全部变为 \(0\),然后将 \([1,x]\) 和 \([x+1,n]\) 分治求解。
很显然对于每个区间 \([l,r]\) ,将 \(x\) 设为 \(\lfloor\frac{l+r}{2}\rfloor\) 时操作次数是最优的。
每次 \(solve(l,r)\) ,我们将 \([l,mid]\) 和 \([mid+1,r]\) 中没有复原的柱子两两匹配,我们令两根柱子分别为 \(i\) 和 \(j\),这样,\(i\) 和 \(j\) 中如果 \(\le mid\) 的个数大于 \(>mid\) 的个数,那么将 \(i\) 还原,否则将 \(j\) 还原,然后继续递归下去 \(solve(l,mid)\) 和 \(solve(mid+1,r)\) 就行了。
计算一下总操作次数:
\[T(n)=2\cdot T(n/2)+5\cdot n\cdot m \]那么
\[T(n)=5\cdot n\cdot m\cdot \log n \]计算一下,这是 \(ok\) 的
#include<bits/stdc++.h>
using namespace std;
const int N=55;
const int M=405;
#define tp(x) a[x][top[x]]
int n,m,tot;
int a[N][M],top[N];
int ans[820005][2];
inline void move(int x,int y){
ans[++tot][0]=x,ans[tot][1]=y;
a[y][++top[y]]=a[x][top[x]--];
}
inline void solve(int l,int r){
if(l==r) return;
int mid=l+r>>1;
bitset <N> vis;
for(int i=l;i<=mid;++i)
for(int j=mid+1;j<=r;++j){
if(vis[i]||vis[j]) continue;
int cnt=0;
for(int k=1;k<=m;++k)
cnt+=(a[i][k]<=mid)+(a[j][k]<=mid);
if(cnt>=m){
cnt=0;
for(int k=1;k<=m;++k) cnt+=(a[i][k]<=mid);
for(int k=1;k<=cnt;++k) move(j,n+1);
while(top[i]) move(i,tp(i)<=mid?j:n+1);
for(int k=1;k<=cnt;++k) move(j,i);
for(int k=1;k<=m-cnt;++k) move(n+1,i);
for(int k=1;k<=m-cnt;++k) move(j,n+1);
for(int k=1;k<=m-cnt;++k) move(i,j);
while(top[n+1]) move(n+1,(top[i]!=m&&tp(n+1)<=mid)?i:j);
vis[i]=1;
}
else{
cnt=0;
for(int k=1;k<=m;++k) cnt+=(a[j][k]>mid);
for(int k=1;k<=cnt;++k) move(i,n+1);
while(top[j]) move(j,tp(j)>mid?i:n+1);
for(int k=1;k<=cnt;++k) move(i,j);
for(int k=1;k<=m-cnt;++k) move(n+1,j);
for(int k=1;k<=m-cnt;++k) move(i,n+1);
for(int k=1;k<=m-cnt;++k) move(j,i);
while(top[n+1]) move(n+1,(top[j]!=m&&tp(n+1)>mid)?j:i);
vis[j]=1;
}
}
solve(l,mid),solve(mid+1,r);
}
signed main(){
cin>>n>>m;
for(int i=1;i<=n;++i) for(int j=1;j<=m;++j)
cin>>a[i][++top[i]];
solve(1,n);
cout<<tot<<endl;
for(int i=1;i<=tot;++i)
cout<<ans[i][0]<<" "<<ans[i][1]<<endl;
}