标签：分析 int 复杂度 算法 循环 时间 空间

时间复杂度

「时间复杂度」(Time complexity)定性描述该算法的运行时间

• 大O符号表示法(BigO))：

T(n) = O(f(n))

表示一个算法的渐进时间复杂度，f(n)表示代码次数之和，O表示正比例关系

for (int i = 1; i <= i;i++) {
    x++;
}

因为循环次数为n，时间为n单位，所以算法的「时间复杂度」可以表示为：T (n) = O(n)。

O(n²)

i总共需要n层循环，在每一次内层循环中，j 也会循环n次

for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= n; j++) {
        x++;
    }
}

O(n + n²)

上面两个算法并和：

for (int i = 1; i <= n; i++) {
    x++;
}
for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= n; j++) {
        x++;
    }
}

整个算法复杂度就变为 O(n + n²)，在n无限大的情况下，可以简化为 O(n²)。

常见的时间复杂度量级

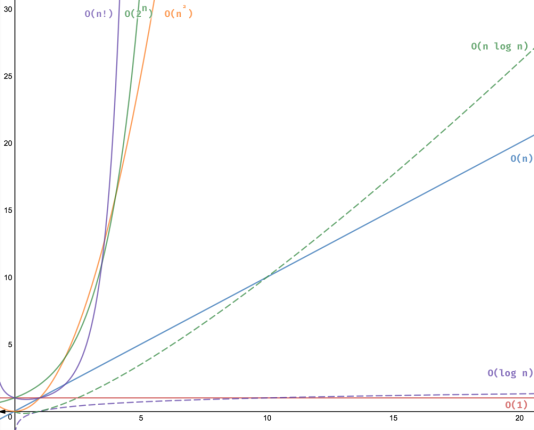
常数阶O(1)

int x = 0;
int y = 1;
int temp = x;
x = y;
y = temp;

对数阶O(logN)

int i = 1;
while(i < n) {
    i = i * 2;
}

线性阶O(n)

for (int i = 1; i <= n; i++) {
    x++;
}

对数阶O(logN)

int i = 1;
while(i < n) {
    i = i * 2;
}

线性对数阶O(nlogN)

for(int i = 0; i <= n: i++) {
    int x = 1;
    while(x < n) {
        x = x * 2;
    }
}

平方阶O(n²)

for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= n; j++) {
        x++;
    }
}

立方阶O(n³)

for(int i = 1; i <= n; i++) {
    for (int j = 1; j <= n; j++){
        for(int k = 1; k <= n; k++){
            s++;
        }
    }
}

K次方阶O(n^k)

k次方阶就相当于在有k层for循环

指数阶O(2^n)

public int aFunc(int n) {    
   if (n <= 1) {        
       return 1;
   } else {        
       return aFunc(n - 1) + aFunc(n - 2);
   }
}

阶乘O(n!)

void nFacRuntimeFunc(int n) {
  for(int i=0; i<n; i++) {
    nFacRuntimeFunc(n-1);
  }
}

其他还有「平均时间复杂度」、「均摊时间复杂度」、「最坏时间复杂度」、「最好时间复杂度]......

空间复杂度

「空间复杂度」(Computational problem)表示一个算法完全执行所需要的存储空间大小

常用的空间复杂度

O(1)空间复杂度

int x = 0;
int y = 0;
x++;
y++;

代码中的 i、j、m 所分配的空间都不随着处理数据量变化，因此它的空间复杂度 S(n) = O(1)

空间复杂度 O(n)

int[] m = new int[n]
for(i=1; i<=n; ++i)
{
   j = i;
   j++;
}

这段代码的空间复杂度主要看第一行即可，即 S(n) = O(n)

标签：分析,int,复杂度,算法,循环,时间,空间
From： https://www.cnblogs.com/wrxinyue/p/16935679.html