标签：log int 笔记二叉学习 heap 操作节点

二叉堆

在谈二叉堆之前，先来叙述一下堆的概念。

堆，听起来可能与栈的结构差不多（?），但是堆其实是一棵树。这棵树的根就是堆顶，一般堆顶就是用来维护答案的（e.g. 最大值、最小值）。

如果根节点是最大值，则称该堆为最大堆（大根堆）；如果根节点是最小值，则称该堆为最小堆（小根堆）。

堆一般用二叉树实现，称为二叉堆。

二叉堆的典型应用：堆排序与优先队列。

二叉堆的概念

二叉堆本质上是一棵完全二叉树。用数组实现的二叉堆，书中的每个节点与数组中存放的每个元素相对应。

完全二叉树指的就是这棵二叉树的每层，除了最后一层可能不是满的，其他都是满的。

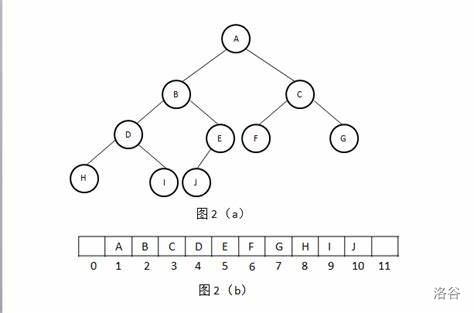
上图（图一）为用数组实现二叉堆的示意图。

二叉堆中的每个节点，都是以它为根节点的子树的最值。

用数组 \(f\) 储存这棵完全二叉树，节点数量为 \(n\)，\(f_1\) 为根节点，则有以下性质：

对于一个 \(i > 1\) 的节点，其父亲节点位于 \(i \div 2\)。
如果 \(2 \times i > n\)，那么节点 \(i\) 没有儿子；如果 \(2 \times i + 1 > n\)，那么节点 \(i\) 没有右儿子。
如果节点 \(i\) 有儿子，则它的左儿子位于 \(2 \times i\)，右儿子位于 \(2 \times i + 1\)。

堆的操作十分简单，只有进堆和出堆。

进堆：每次都把元素插进堆里，只不过要保证插入完成后该堆依旧是一棵完全二叉树，插入完成后，调整堆的形态，保持堆符合最大堆或最小堆的特点。
出堆：即删除根节点。删除根节点后调整堆的形态，保持堆符合最大堆或最小堆的特点。

二叉堆的操作

在【二叉堆的概念】提到了堆的两种操作。

其实这两种操作准确的来讲是上浮与下沉。

上浮

定义：如果这个节点的权值大于它父亲的权值，就交换，重复此过程直到不满足或者到根。

堆的进堆过程中，插入操作最简单的方式就是把元素插入到最低层的最右侧。若最底层已满，则新建一层。

上图（图二）为最大堆的上浮过程示意图。

可以证明，插入之后向上调整后，没有其他节点会不满足堆性质。

时间复杂度：\(O(\log n)\)。

下沉

定义：在该节点的儿子中，找一个最大的，与该节点交换，重复此过程直到底层。

我们不妨想象，直接删除根节点的话，就会变成两个堆，很难处理。

所以不妨考虑插入操作的逆过程，设法将根节点移到最后一个节点，然后直接删掉。
然而实际上不好做，我们通常采用的方法是，把根节点和最后一个节点直接交换。

但是在交换节点后，如果直接删除交换后的根节点的话，堆将会不满足堆性质。

可以证明，删除并向下调整后，没有其他节点不满足堆性质。

应为上文已经出示过上浮的示意图，所以这里不在展示下沉的示意图了。（下沉就是上浮的逆操作）

时间复杂度：\(O(\log n)\)

更改某个点的权值

如果是减小的话，那么直接将该节点上浮就可以了。

如果是增大的话，那么直接将该节点下沉就可以了。

时间复杂度：\(O(\log n)\)

实现

根据上文，我们知道二叉堆主要依靠的就是上浮与下沉操作。

所以我们根据完全二叉树的性质，考虑使用数组 \(h_i\) 表示该堆，即 \(h_{2i}\) 表示 \(i\) 的节点的左儿子，\(h_{2i + 1}\) 表示 \(i\) 节点的右儿子。\(1\) 是根节点。

上浮

void up(int x)
{
    while (x > 1 && h[x] > h[x / 2])
    {
        swap(h[x], h[x / 2]);
        x /= 2;
    }
}

下沉

void down(int x)
{
    while (x * 2 <= n)
    {
        t = x * 2;
        if (t + 1 <= n && h[t + 1] > h[t])
            t ++;
        if (h[t] <= h[x])
            break;
        swap(h[x], h[t]);
        x = t;
    }
}

建堆

建堆其实可以想象成 \(n\) 个节点依次插入堆。

所以就有两种操作：

一：向上调整
二：向下调整

方法一

从根开始，按照 BFS 序依次插入进堆。然后进行向上调整操作。

void BuildHeap()
{
    for (i = 1; i <= n; i ++)
        up(i);
}

总复杂度：
\(\log 1 + \log 2 + \log 3 + \cdots + \log n = O(n \log n)\)。

方法二

从叶子开始，依次进行向下调整操作。

void BuildHeap()
{
    for (i = n; i >= 1; i --)
        down(i);
}

如此做就相当于：每次合并两个已经调整好的堆（即满足堆性质的堆），这已经说明该算法的正确性。

我们可以看出这种方式的复杂度为 \(O(\log n - k)\)。另外假如题目数据较紧，我们可以想：叶子节点无需调整，所以只需要从序列约 \(\dfrac{n}{2}\) 的位置开始向下调整即可。

总复杂度：
\(n \log n - \log 1 - \log 2 - \log 3 - \cdots - \log n\) = \(O(n)\)。

具体过程见 OI Wiki。

模板题

Description

现有一个空的小根堆，并有以下三种操作：

输入 1 x，表示将 \(x\) 插入堆中。
输入 2，则输出该小根堆内的最小数。
输入 3，表示删除该小根堆内的最小数。

Input

第一行一个整数 \(n\)，表示操作个数。

接下来 \(n\) 行，每行 \(1\) 或 \(2\)，个正整数，表示进行的操作。

Output

对于每个操作 2，输出一个整数表示答案（每两个答案之间空一行）。

Limit

\(n \le 10^6\)，保证操作是三种操作之一。

Code

下面给出代码，读者可以根据上文自行理解。

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6 + 5;
int n, len;
int heap[maxn];

void up(int x)
{
    heap[++ len] = x;
    int i = len;
    while (i > 1 && heap[i] < heap[i / 2])
    {
        swap(heap[i], heap[i / 2]);
        i = i / 2;
    }
}

void down()
{
    heap[1] = heap[len --];
    int i = 1;
    while (2 * i <= len)
    {
        int son = 2 * i;
        if (son < len && heap[son + 1] < heap[son])
            son ++;
        if (heap[son] < heap[i])
        {
            swap(heap[son], heap[i]);
            i = son;
        }
        else
            break;
    }
}

int main()
{
    int n;
    scanf("%d", &n);
    while (n --)
    {
        int opt;
        scanf("%d", &opt);
        if (opt == 1)
        {
            int x;
            scanf("%d", &x);
            up(x);
        }
        else if (opt == 2)
            printf("%d\n", heap[1]);
        else
            down();
    }
}

参考文献

OI Wiki
图一 - CsdnUser 014182411
图二 - OIWiki
图三 - OIWiki
《算法竞赛（罗勇军、郭卫斌）》

标签：log,int,笔记,二叉,学习,heap,操作,节点
From： https://www.cnblogs.com/mrCrazyWolf/p/16928285.html

【学习笔记】二叉堆

二叉堆