前言
今天浅试了一下vscode的typora插件和cnblog插件,这篇文章是typora插件编写,cnblog插件发布的
Problem
题目描述
给定一颗 \(n\) 个节点的树。\(q\) 次询问,每次询问给定两个点 \(x,y\) ,保证 \(x\not=y\) ,你需要求有多少有序四元组 \((a,b,c,d)\) 满足,点 \(a,b\) 之间简单路径与 \(c,d\) 之间的简单路径的交集恰好为 \(x,y\) 之间的简单路径。
你只需要输出答案对 \(998244353\) 取模后的结果即可。
有序四元组:并没有什么特殊含义,定义任意两个四元组不同当且仅当四个元素至少一个元素不同,例如(b,a,c,d)和(a,b,c,d)为两个不同的四元组
输入格式
第一行两个数,\(n,q\)。
接下来 \(n-1\) 行,每行 \(u,v\) 代表 \(u\) 和 \(v\) 之间有一条树边。
接下来 \(q\) 行,每行输入 \(x,y\) 代表一次询问
输出格式
输出 \(q\) 行,第 \(i\) 行为第 \(i\) 次询问的答案取模 \(998244353\) 后的结果。
Solution
个人感觉这题比T1简单一点
不难想到这个题有分为两种情况讨论。下面所讲的 \(x,y\) 默认 \(y\) 的深度低于 \(x\) 的深度,以 \(1\) 为根节点的情况。
下面所说的合法的选取方案是指:以 \(u\) 为根节点的子树取任意两个来自不同儿子的子树点的方案数
Case 1
\(y\) 不为 \(x\) 的祖先。
对于这种情况比较显然,我们可以在树上dfs的过程中预处理对于以任意节点 \(u\) 作为根节点时合法的选取方案数,具体的,如下图,我们可以枚举每一个儿子节点 \(v\),然后从其他点中入选一个。
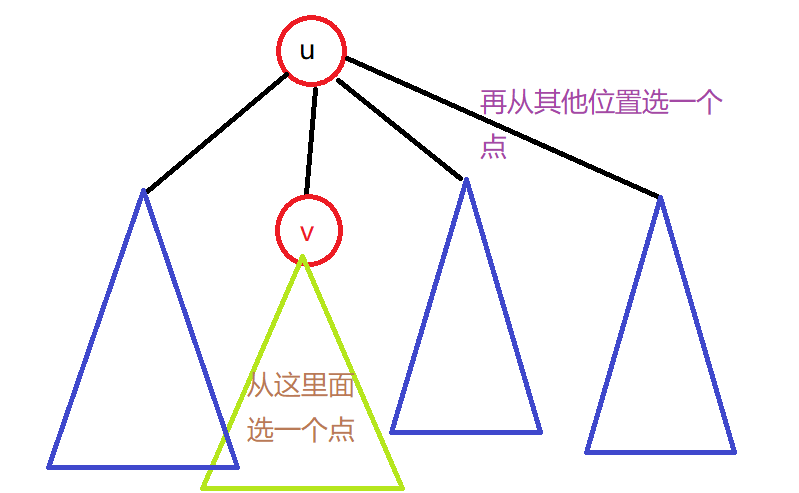
需要注意的是由于没选两个点的情况会重复,所以统计完需要除 \(2\) (这里我们需要用到 \(2\) 模 \(998244353\) 情况下的逆元),还需要特殊考虑选择 \(u\) 节点并从子树中任选一个点的情况。部分代码如下(我用的是vector存图,xun2[u]代表从 \(u\) 为根的子树中选两个合法点的方案数)
for(int i=0;i<edge[u].size();++i){//计算选2个点的情况
int v=edge[u][i];
if(v==fat) continue;
xun2[u]+=(siz[v])*(siz[u]-siz[v]-1)%mod;
xun2[u]%=mod;
}
xun2[u]=(xun2[u]*inv2%mod);//除2
xun2[u]=(xun2[u]+siz[u]-1)%mod;//选u和子树中任意点的情况
对于这种情况求方案答案代码:(比较显然,思路就不讲了,有不懂的留言)
ans=xun2[x]*xun2[y]%mod*16ll%mod;//2 2
ans=(ans+8*(xun2[y]+xun2[x])%mod)%mod;
ans=(ans+4)%mod;
Case2
\(y\) 为 \(x\) 的祖先。
显然有一种暴力做法,就是对于 \(x\) 和 \(y\) 路径上的点作为根节点然后做Case1的预处理,显然会超时。
考虑预处理对于节点 \(u\) ,删去儿子 \(v\) ,增加儿子 \(fa_u\) 后合法选取两个节点的方案数(其中 \(fa_u\) 为 \(u\) 的父节点)。
比较显然的,我们可以减去 \(v\) 的贡献 ,并加上 \(fa_u\) 的贡献,思路比较简单,详情见代码:
int onx=n-siz[u];//u为根节点子树除外的点数
for(int i=0;i<edge[u].size();++i){//预处理Case2情况,其中x_sum[u][i]为以u为根的子树删去i儿子添加fa[u]后合法选取两个点的方案数
int v=edge[u][i];
if(v==fat) continue;
x_sum[u][i]=((xun2[u]-siz[v]*(siz[u]-siz[v])%mod)%mod+mod)%mod;//减去儿子v的贡献
x_sum[u][i]=(x_sum[u][i]+onx*(siz[u]-siz[v])%mod)%mod;//加上新儿子fa[u]的贡献
}
求答案方法与Case1一样,只是多了个寻找 \(x\) 到 \(y\) 的路径中 \(y\) 的儿子节点的过程,用倍增从 \(x\) 往上条即可。
int yt=jump(x,dep[y]+1);
int idt=lower_bound(edge[y].begin(),edge[y].end(),yt)-edge[y].begin();
int xun2y=x_sum[y][idt];
ans=xun2[x]*xun2y%mod*16ll%mod;//2 2
ans=(ans+8*(xun2y+xun2[x])%mod)%mod;
ans=(ans+4)%mod;
CODE
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=3e5+7;
const int mod=998244353;
int n,q;
vector<int> edge[N];
vector<int> x_sum[N];
int fa[N][22];
int dep[N],siz[N];
int xun2[N];
int ksm(int x,int y){
int res=1,xt=x;
while(y){
if(y&1) res=(res*xt)%mod;
y>>=1;
xt=(xt*xt)%mod;
}
return res;
}
int inv2=ksm(2,mod-2)%mod;
void dfs(int u,int fat){
fa[u][0]=fat;
dep[u]=dep[fat]+1;
siz[u]=1;
for(int i=1;i<=20;++i){
fa[u][i]=fa[fa[u][i-1]][i-1];
}
for(int i=0;i<edge[u].size();++i){
int v=edge[u][i];
if(v==fat) continue;
dfs(v,u);
siz[u]+=siz[v];
}
for(int i=0;i<edge[u].size();++i){//计算选2个点的情况
int v=edge[u][i];
if(v==fat) continue;
xun2[u]+=(siz[v])*(siz[u]-siz[v]-1)%mod;
xun2[u]%=mod;
}
xun2[u]=(xun2[u]*inv2%mod);//除2
xun2[u]=(xun2[u]+siz[u]-1)%mod;//选u和子树中任意点的情况
int onx=n-siz[u];
for(int i=0;i<edge[u].size();++i){//预处理Case2情况,其中x_sum[u][i]为以u为根的子树删去i儿子添加fa[u]后合法选取两个点的方案数
int v=edge[u][i];
if(v==fat) continue;
x_sum[u][i]=((xun2[u]-siz[v]*(siz[u]-siz[v])%mod)%mod+mod)%mod;//减去儿子v的贡献
x_sum[u][i]=(x_sum[u][i]+onx*(siz[u]-siz[v])%mod)%mod;//加上新儿子fa[u]的贡献
}
// xun2[u]%=mod;
}
int LCA(int u,int v){
if(dep[u]<dep[v]) swap(u,v);
for(int i=20;i>=0;--i){
if(dep[fa[u][i]]>=dep[v]){
u=fa[u][i];
}
}
if(u==v) return u;
for(int i=20;i>=0;--i){
if(fa[u][i]!=fa[v][i]){
u=fa[u][i];v=fa[v][i];
}
}
return fa[u][0];
}
int jump(int u,int dept){
for(int i=20;i>=0;--i){
if(dep[fa[u][i]]>=dept){
u=fa[u][i];
}
}
return u;
}
// int get_xun2(int u,int son){
// int sizt=siz[1]-siz[son];
// return sizt;
// }
signed main(){
clock_t st,ed;
st=clock();
freopen("path.in","r",stdin);
freopen("path.out","w",stdout);
scanf("%lld%lld",&n,&q);
for(int i=1;i<n;++i){
int u,v;
scanf("%lld%lld",&u,&v);
edge[u].push_back(v);
edge[v].push_back(u);
x_sum[u].push_back(0);
x_sum[v].push_back(0);
}
for(int i=1;i<=n;++i){
sort(edge[i].begin(),edge[i].end());
}
dfs(1,0);
while(q--){
int x,y;
scanf("%lld%lld",&x,&y);
if(dep[x]<dep[y]) swap(x,y);
int lcat=LCA(x,y);
int ans=0;
if(lcat==y){
int yt=jump(x,dep[y]+1);
int idt=lower_bound(edge[y].begin(),edge[y].end(),yt)-edge[y].begin();
int xun2y=x_sum[y][idt];
ans=xun2[x]*xun2y%mod*16ll%mod;//2 2
ans=(ans+8*(xun2y+xun2[x])%mod)%mod;
ans=(ans+4)%mod;
}else{
ans=xun2[x]*xun2[y]%mod*16ll%mod;//2 2
ans=(ans+8*(xun2[y]+xun2[x])%mod)%mod;
ans=(ans+4)%mod;
}
printf("%lld\n",ans);
}
ed=clock();
// cout<<"run:"<<ed-st<<"ms"<<endl;
return 0;
}