费用流

标签：费用 int cap vis ans dis

title: 费用流
tags: 算法

本文章遵守知识共享协议 CC-BY-NC-SA ，转载时需要署名，推荐在我的个人博客阅读。

简介

费用流是网络流的拓展，一般用于求解一些多次取点的问题。

前置知识

• 网络流
• 最短路

讲解

定义

在网络流中，在花费费用最小时的最大流。

如果有冲突，则优先满足最大流。

实现

大体逻辑和网络流区别不大，只是将算法中的 bfs 改为spfa或其他最短路算法，以费用为边权搜索最短路。

费用流算法可以基于 EK 和 Dinic 改来，下面这一版是基于 Dinic 更改而来的。

bool spfa(int s, int t) {
  memset(dis, 0x3f, sizeof(dis)); // 初始化距离数组
  memcpy(cur, lnk, sizeof(lnk)); // 复制数组状态
  queue<int> q;  // 正常的spfa
  q.push(s), dis[s] = 0, vis[s] = 1;
  while (!q.empty()) {
    int u = q.front();
    q.pop(), vis[u] = 0;
    for (int i = lnk[u]; i; i = nxt[i]) {
      int v = ter[i];
      if (cap[i] && dis[v] > dis[u] + cost[i]) {
        dis[v] = dis[u] + cost[i];
        if (!vis[v]) q.push(v), vis[v] = 1;
      }
    }
  }
  return dis[t] != INF; // 代表是否可以到达汇点
}

int dfs(int u, int t, int flow) {
  if (u == t) return flow;
  vis[u] = 1;
  int ans = 0;
  for (int &i = cur[u]; i && ans < flow; i = nxt[i]) {
    int v = ter[i];
    if (!vis[v] && cap[i] && dis[v] == dis[u] + cost[i]) {
      int x = dfs(v, t, min(cap[i], flow - ans));
      if (x)
        ret += x * cost[i], 
        cap[i] -= x,
        cap[i ^ 1] += x, ans += x;
    }
  }
  vis[u] = 0;
  return ans;
}

int solve(int s, int t) {
  int ans = 0;
  while (spfa(s, t)) {
    int x;
    while ((x = dfs(s, t, INF))) ans += x;
  }
  return ans;
}

例题

P1004-[NOIP2000-提高组]-方格取数

这道题的难点在于构建费用流网络，首先分析题目性质：

• 一个格子只能取一次数字
• 可以走多次

根据这些可以构建出第一个图：

在每个点的连接处连流量为 $2$ ，费用为 $-val_i$ 的边，然后跑最大流。

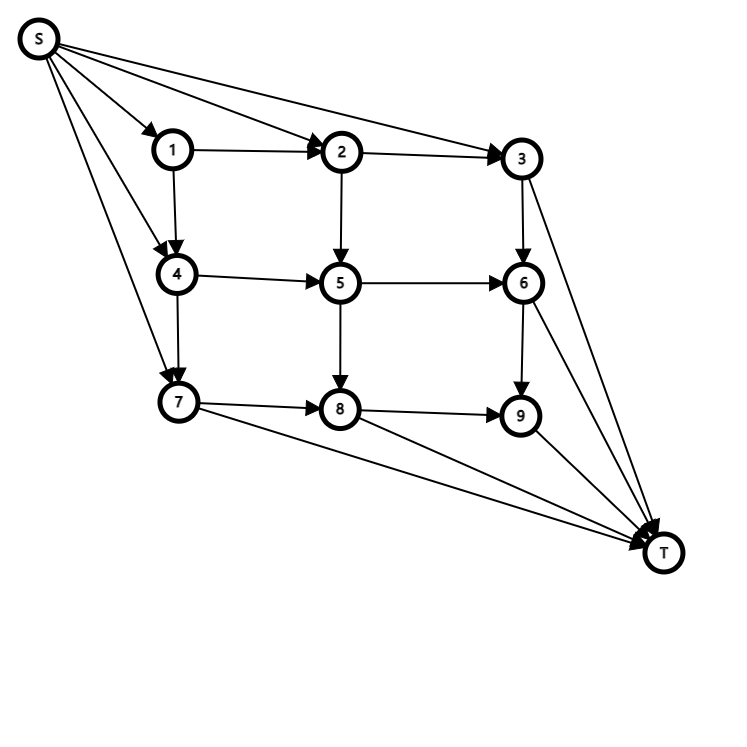
先别急着翻到下面去，这个构建方法显然是错误的，因为没有考虑到走的次数，并且一个点可能被统计多次。

所以便有了下面这种方法。

我们使用拆点的方法，将一个点拆成两个，点中间连接流量为 $2$，费用为 $-val_i$ 的边，然后跑最大流。

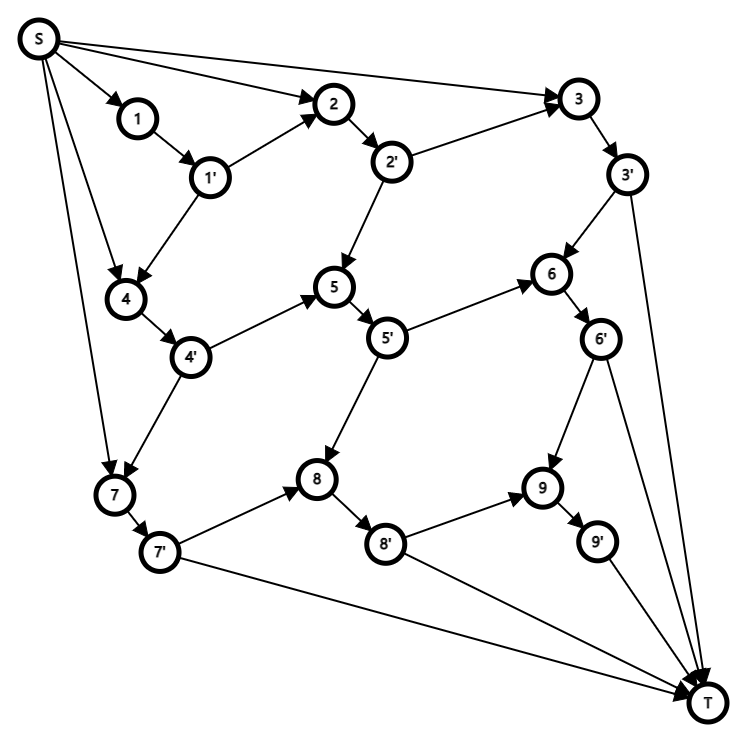
当然，它还是错的。

继续想更正思路，我们需要再次拆S,T点并添加限流才能确保没问题。

还有一点就是像 1->1' 这里要连两条边，第一条容量 $1$ 费用 $0$ 确保联通，第二条容量 $1$ 费用 $-val_i$ 才是实际能取到的价值

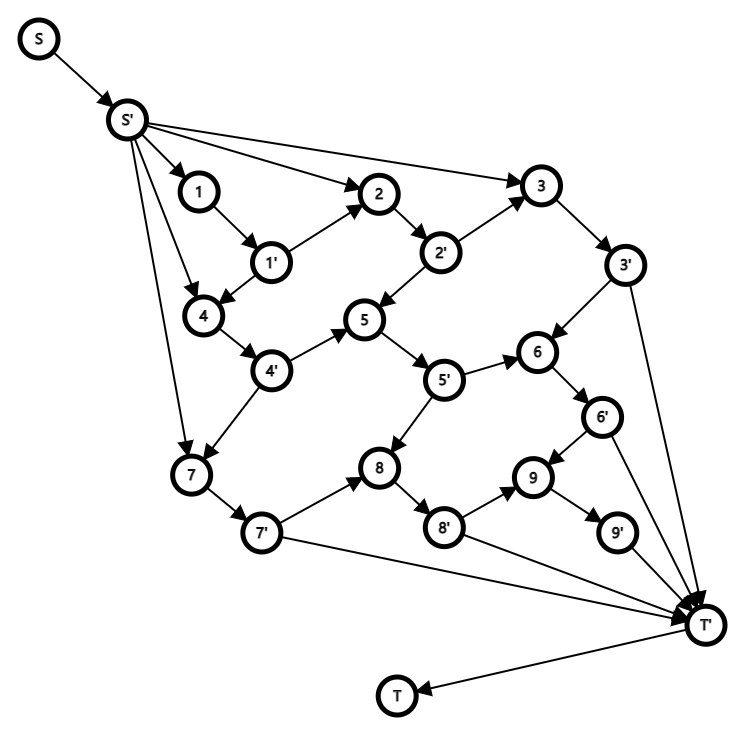
最后的图就是这样。

其实不管是网络流，还是费用流，最难的部分都是构建图，需要多理解为什么这么构建才能。

P1000-A+B-Problem

同样简单的讲解一下。

标签：费用,int,cap,vis,ans,dis
From： https://www.cnblogs.com/rickyxrc/p/16921522.html