目录
linux基础命令
ls--查看当前目录下所有文件
cd--切换目录
cp--复制文件
mv--移动文件
touch--建立新文件
rm--删除文件
-- -r:递归删除,主要用于删除目录,可删除指定目录及包含的所有内容,包括所有的子目录和文件
进制转换
各种转换间的运算QAQ--知乎(图片及参考源于此处)
进制转换--百度百科
- 十进制: 都是以0-9这九个数字组成,不能以0开头。
- 二进制: 由0和1两个数字组成。
- 八进制: 由0-7数字组成,为了区分与其他进制的数字区别,开头都是以0开始。
- 十六进制:由0-9和A-F组成。为了区分于其他数字的区别,开头都是以0x开始。
Method
十转x进制:
-
将需要转换的数(a)除以x,取余--a % x,余数为所求进制数,从下往上取
-
所的整数部分保留,重复步骤1,直到商为0
例如:9(十进制)→1001(二进制)
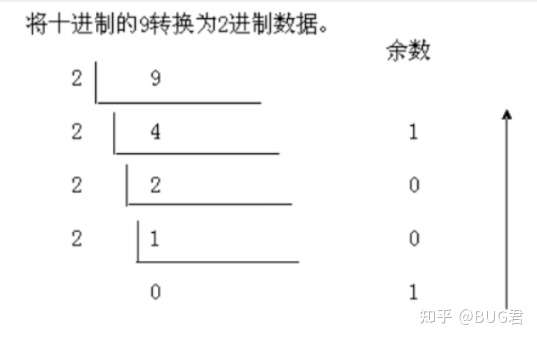
小数部分转化
十转二:
原理:十进制小数转换成二进制小数采用 “乘2取整,顺序输出” 法。
例题: 0.68D = ______ B(精确到小数点后5位)
如下所示,0.68乘以2,取整,然后再将小数乘以2,取整,直到达到题目要求精度。得到结果:0.10101B.
例如:十进制小数0.68转换为二进制数
具体步骤:
0.68* 2=1.36 -->1
0.36* 2=0.72 -->0
0.72* 2=1.44 -->1
0.44* 2=0.88–>0
0.88* 2=1.76 -->1
已经达到了题目要求的精度,最后将取出的整数部分顺序输出即可
则为:0.68D–>0.10101B
其他进制思路一样,小数与整数结合的,两种方法直接一起套用
二进制、八进制、十六进制转换为十进制

小数部分:小数部分从小数点后一位指数-1为开始算起,以后依次为-2、-3……
排序算法
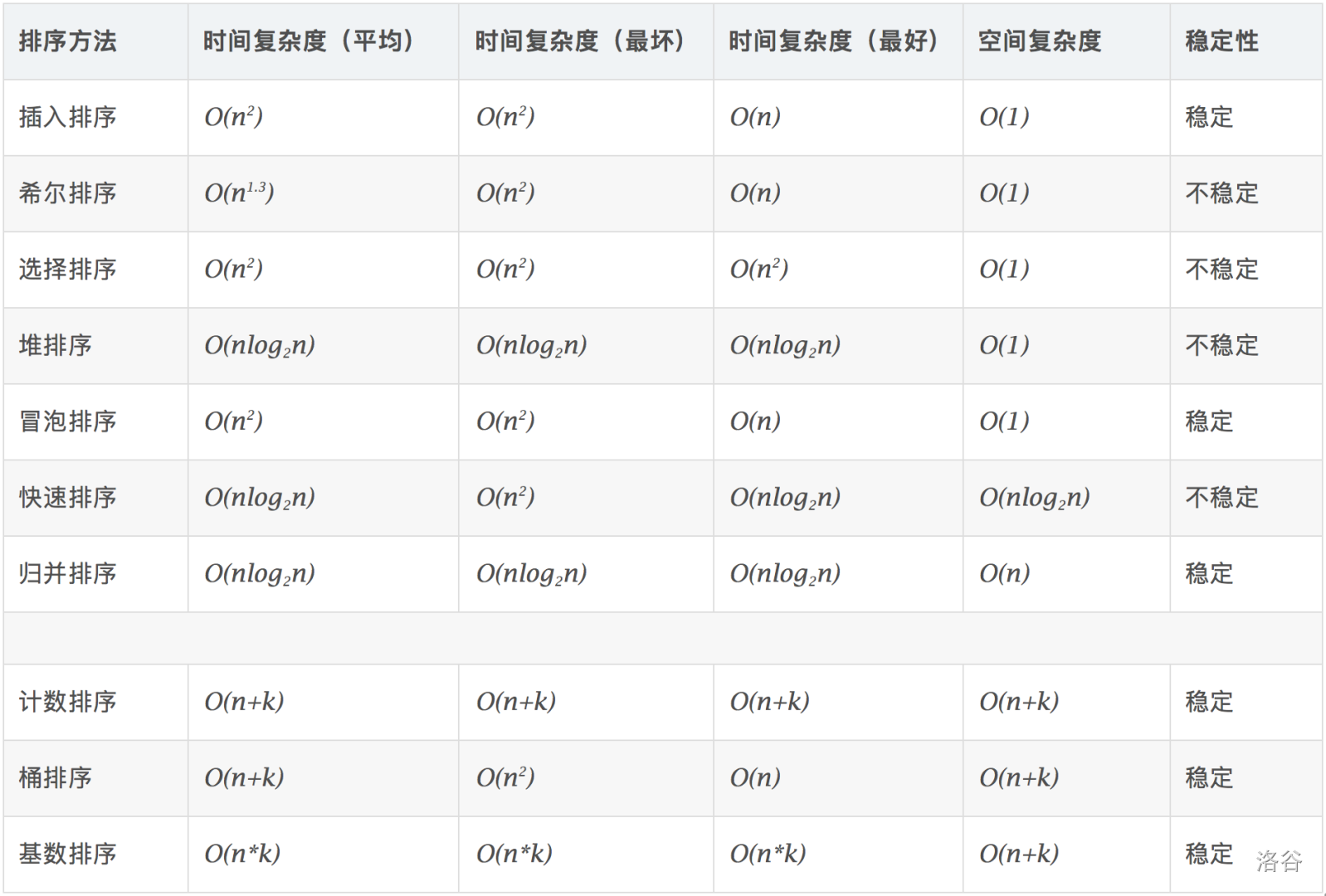
原码、补码、反码、计算
个人感觉,这篇文章讲的十分清楚了-----https://www.cnblogs.com/zhangziqiu/archive/2011/03/30/ComputerCode.html#!comments
计算
正数与正数:计算直接各位对应相加,二进制满二进一,
负数与正数 or 负数与负数:都转换为补码,符号位不变,直接相加,再转换回原码即可(原码的补码后再补码等于其本身)
注:原码和补码范围为[ -127, 127 ],而补码为[ -128, 127 ],因为原码与补码中,对0有两种表示,即正负0,而补码中正负0均表示为 0000 0000 ,补码中 1000 0000,表示-128
1、[+0]原码=0000 0000, [-0]原码=1000 0000
2、[+0]反码=0000 0000, [-0]反码=1111 1111
3、[+0]补码=0000 0000, [-0]补码=0000 0000
正数三码和一
为什么要有反码? 为了解决原码做减法的问题
为什么要有补码? 为了解决正负0同一个编码的问题
有了补码,反码还有作用吗?
可能真的没什么作用了,只是作为原码到补码的过度状态 ?可以简单地理解为原码到补码是一个层层递进的关系,也是一个在错误中逐步发展的过程。也就是说利用原码运算减法时出现的错误,为了解决出现了反码运算,但是反码运算时又出现了让人不满意的地方,于是为了更好的追求出现了补码。作者:chenhong_f1e2
链接:https://www.jianshu.com/p/75a490598270
来源:简书
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
运算符
按位与(&)
参加运算的两个数,换算为二进制(0、1)后,进行与运算。只有当相应位上的数都是1时,该位才取1,否则该位为0。
按位或(|)
参加运算的两个数,换算为二进制(0、1)后,进行或运算。只要相应位上存在1,那么该位就取1,均不为1,即为0。
按位异或(^)
参加运算的两个数,换算为二进制(0、1)后,进行异或运算。只有当相应位上的数字不相同时,该为才取1,若相同,即为0。
任何数与0异或,结果都是其本身。
异或还可以交换两个数
a = a ^ b;
b = b ^ a;
a = a ^ b;
取反(~)
参加运算的两个数,换算为二进制(0、1)后,进行取反运算。每个位上都取相反值,1变成0,0变成1。
左移(<<)
x<<n = x*2^n
右移(>>)
x>>n = x/2^n
[csp2019初赛解析]原文链接:https://blog.csdn.net/Skyn_xwm/article/details/102637500
标签:0000,运算,--,汇总,补码,基础知识,二进制,CSP,原码 From: https://www.cnblogs.com/HLlll-blog/p/16624423.html