线段树是个好东西,首先要知道这些点:
1.线段树适用于任何区间修改和区间查询的操作,复杂度只有 O(logn) 贼快
2.线段树没有树状数组好写呢,其实也不难
3.线段树每一个点是管理一个区间!!
4.线段树不是所有节点都代表原数组的一个值,他可能会代表一个区间段中你想要的值
基础理论
首先上一个图

简单了解一下线段树
发现每一个节点的管理区间就是左右子所管理的区间相加
再看下一张图

将节点按照层序遍历编好号,发现:
一个节点的左孩子是它的编号的两倍,它的右孩子的编号是它的两倍加一
叶子节点管理的区间就只有它自己
深入学习
开始考虑修改
如果你使用前缀和去完成线段树的题目线段树模板1的话,你会发现:我c,还有修改!还特么是区间修改
然后你会愉快地 TLE 然后放弃并失去信心
下面就需要线段树了
线段树进行单点修改时,其他子树上的节点根本就不用动!改它干嘛!
例如,你要改原数组中的第6个↓

那么你只用去改变节点 18、12、6、3、1 的区间和的值不就完了!什么4、5、10、11,一点关系都没有!
区间更改也能解决,不过需要一些其他的东西。
实现
首先看一看如何建树!
本文只介绍静态建点、递归建树!
先定义一个结构体:
struct st
{
int s;
int l,r;
int lazy;
};
这个结构体就是一个节点!
l 和 r 分别代表这个节点管理的区间的左端点与右端点
s 是指它这个节点所管理的区间的和是多少
建树部分:
void buildtree(int i,int left,int right)
{
t[i].l=left;
t[i].r=right;
if(left==right)
{
t[i].s=a[left];
return ;
}
int mid=(left+right)/2;
buildtree(lson,left,mid);
buildtree(rson,mid+1,right);
t[i].s=t[lson].s+t[rson].s;
}
首先:
参数left和right代表即将建树的部分
i代表你已经到的节点编号
接下来就可以快乐的把节点 i 的 l 和 r 赋值为 left 和 right了
如果i为叶子结点,也就是left==right时,直接把它的区间和赋值为a[left]
为什么是a[left]呢?
因为到了叶子结点,他所管理的就是他自己
算了,还是来张图吧:
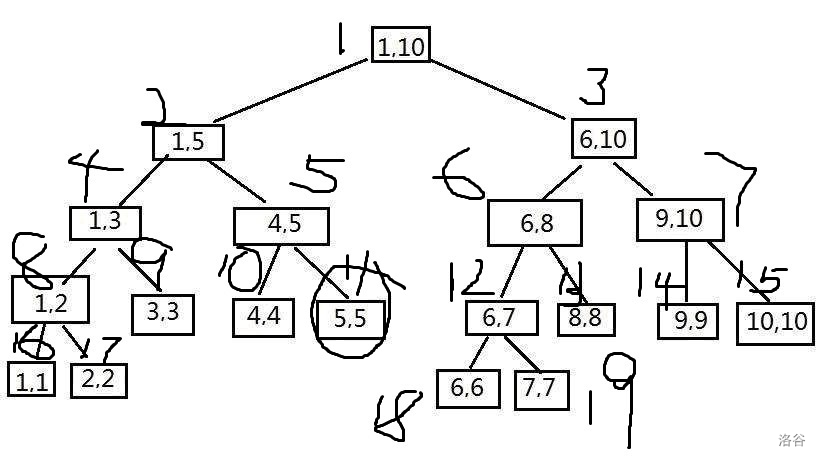
比如说你要建第11个节点
看他的 l 和 r
发现都为5
所以直接赋值吧!毕竟它就是管理数组中下标为5的数
然后继续往下建树
根据上面的那张图可以发现:
他的左儿子管理的区间是 l 到 (l + r) / 2 ,右儿子是 (l+r)/2+1 到 r
所以向下建树吧
最后一步将左儿子的区间和加上右儿子的区间和就好了!
单点修改
在这里只阐述原理,不放出代码
先找到一个数
比如说第5个数:
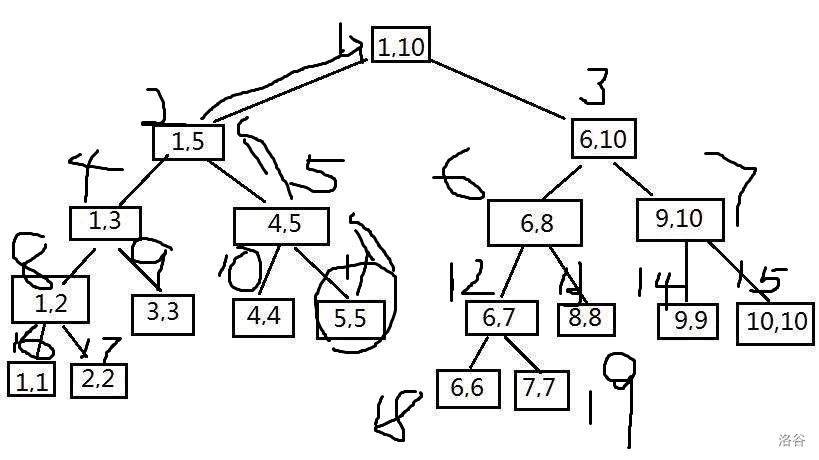
更改以后也会更改的点有:5 2 1
所以只用把这些节点更改就完了
找到这个节点,再往根节点上去,将路途中的所有节点pushup一遍就完了
区间修改!!重中之重
讲区间修改之前,先简单讲讲懒惰标记
懒惰标记
懒惰标记是一个很好的东西,它好就好在可以降低区间修改的复杂度
具体是怎么用,是什么,接着看:
比如说我要修改区间26(居然一直在用一个图,我真勤奋~)
我都懒得上图了,直接翻翻上面的
我们会发现第9,5,18个节点会被覆盖
再看一眼结构体:
struct st
{
int s;
int left;
int right;
int lazy;
}t[maxn*4];
有没有好奇那个lazy是干什么用的
那个lazy就是懒惰标记
当你发现当前节点所管理的区间已被需要修改的区间覆盖
立即停止,将懒惰标记加上你所需要增加的值,再把这个节点所管理的区间和更新一下,然后回溯
代码:
void pushdown(int i)
{
if(t[i].lazy==0) return; 不需要更新
if(t[i].left==t[i].right)
{
t[i].lazy=0; 已经到了叶子节点,结束。因为已经改过了,下面也没有左儿子或右儿子了
return ;
}
t[lson].s+=(t[lson].right-t[lson].left+1)*t[i].lazy;将左子更改
t[lson].lazy+=t[i].lazy;懒惰标记继承给左子,为了以后将左子的左子和右子pushdown更新
t[rson].s+=(t[rson].right-t[rson].left+1)*t[i].lazy;同理
t[rson].lazy+=t[i].lazy;
t[i].lazy=0;
}
void change(int i,int left,int right,int d) d为需要加上的数值
{
pushdown(i);
if(t[i].left==left && t[i].right==right)
{
t[i].lazy=d;
t[i].s+=(right-left+1)*d;所需要加上的和为:数量*需要加上的数值
return ;
}
t[i].s+=(right-left+1)*d;
if(t[lson].right>=right) change(lson,left,right,d);判断左子或右子是否有一部分被需要更改的区间覆盖
else if(t[rson].left<=left) change(rson,left,right,d);
else change(lson,left,t[lson].right,d),change(rson,t[rson].left,right,d);
}
如果你要用到i这个节点,你需要先pushdown一下,因为它的左儿子和右儿子都没有更新,所以需要先pushdown更新一下
区间更改 完结撒花★,°:.☆( ̄▽ ̄)/$:.°★ 。
单点查询
与单点更改差不多,自己想一想吧(懒得写了 比较简单)
区间查询
最后一个重点
还是看以前的图吧 ε=ε=ε=┏(゜ロ゜;)┛
接下来查询区间2~6
还是上一张图吧:

需要查询节点17,9,5,18的值
然后向上传递和
代码:
int query(int i,int l,int r)
{
pushdown(i);
if(t[i].left>=l&&t[i].right<=r)
return t[i].s;
int e=0;
if(t[lson].right>=left)判断左子是否有覆盖部分
e+=quert(lson,l,r);有就加上
if(t[rson].left<=right)判断右子是否有覆盖部分
e+=query(rson,l,r);有就加上
return e;上传
}
题目:
全部完结撒瓜!!
题目解析我会再写一篇blog
标签:lazy,right,入门,int,线段,区间,节点,left From: https://www.cnblogs.com/Y2y7m/p/16909475.html