简单说就是xgboost用二阶导数取代了GBDT中的步长,所以迭代的更精确
from:https://zhuanlan.zhihu.com/p/50176849
GBDT和XGBoost两个模型后者在Kaggle中使用的相当频繁。
其实这两者在算法中有着异曲同工之妙。
首先要从泰勒公式讲起:
泰勒公式本身的作用是用来近似的计算函数的值的,那么我们可以使用一阶泰勒展开式和二阶泰勒展开式分别进行推导
泰勒公式的基本形式是
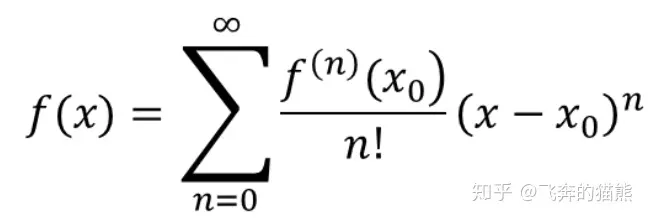
那么一阶的泰勒展开式为:
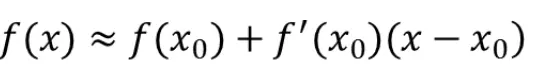
二阶的泰勒展开式为:
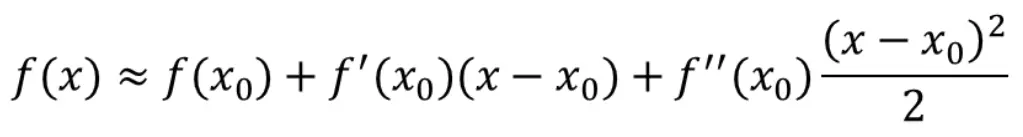
式子本身是使用 x0 代表已知的点去估计 x
迭代形式:
设 xt=xt−1+Δx
那么 f(xt)=f(xt−1+Δx),也就是说在上述的一阶泰勒展开式中 x0=xt−1 和 x=xt
那么式子本身的意义是使用 xt−1 代表已知的点去估计 xt
这时候的二阶展开式为
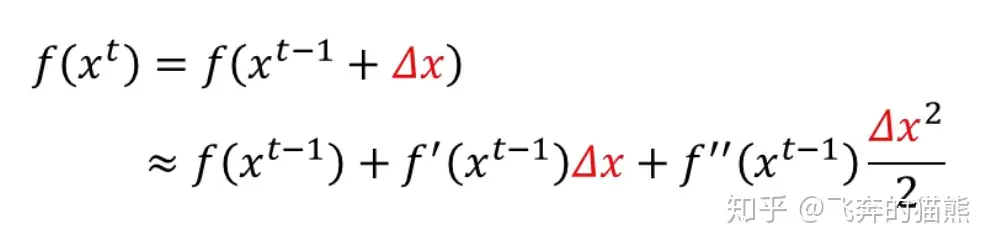
一阶同理
好了泰勒展开式的讲到这里,之后我们要讲从泰勒展开式延伸开的梯度下降法和牛顿法
总的来说梯度下降法和牛顿法分别使用了一阶泰勒展开式和二阶泰勒展开式产生了迭代公式。
1.梯度下降法
定义:梯度下降法(英语:Gradient descent)是一个一阶最优化算法,通常也称为最速下降法。 要使用梯度下降法找到一个函数的局部极小值,必须向函数上当前点对应梯度(或者是近似梯度)的反方向的规定步长距离点进行迭代搜索。
定义的WIKI中文链接:
https://zh.wikipedia.org/wiki/%E6%A2%AF%E5%BA%A6%E4%B8%8B%E9%99%8D%E6%B3%95zh.wikipedia.org/wiki/%E6%A2%AF%E5%BA%A6%E4%B8%8B%E9%99%8D%E6%B3%95也就是说梯度下降法是用来最小化损失函数的 L(θ) ,其中的 θ 是模型参数,求无约束最优化问题,即在给与了初始值后,不断进行迭代。
当我们给与了初始值 θ0 后,
可以得 θt=θt−1+Δθ
代入一阶泰勒展开式,并把函数改成损失函数
L(θt)≈L(θt−1)+L′(θt−1)Δθ
然后是时候开始真正的技术啦
为了使每次迭代的损失函数不断变小,我们使用了一个绝妙的替代:
使用 Δθ=−αL′(θt−1)
这也就产生了
L(θt)≈L(θt−1)−α(L′(θt−1))2
那么这就保证了我们每次迭代都是使损失函数减少的,也就是梯度下降法啦
其中 α 是步长,通过line search决定(也就是暴力搜索 - -!),但是一般都给一个比较小的数。
2. 牛顿法
牛顿法是对泰勒公式的二阶展开搞事情
我们先来看泰勒公式的二阶展开
L(θt)≈L(θt−1)+L′(θt−1)Δθ+L″(θt−1)(Δθ)2/2
仔细看公式还是有点麻烦的,我们先把他简化一下,拿几个字母代替一阶(g)和二阶(h)的结果
L(θt)≈L(θt−1)+gΔθ+h(Δθ)2/2
之后我们需要得到迭代的损失函数比上一次小,换个思路想想,实际上就是求多余部分的极小值,也就是 gΔθ+h(Δθ)2/2 部分,那么针对这部分我们对这部分求差值Δθ导数,
得 Δθ=−g/h
这也就是说 θt=θt−1+Δθ=θt−1−g/h
这就直接出来啦, 迭代公式居然直接反向放到第一步就直接出来啦,朋友们
我们再使用向量的形式进行书写
θt=θt−1−gH−1
其中 H−1 是海森矩阵的逆
OK,我们啰啰嗦嗦讲完了三块:1. 泰勒展开式 2.梯度下降法 3.牛顿法
接下来开始叙述GBDT和XGBoost:
本质上GBDT使用了梯度下降法,XGBoost使用了牛顿法分别进行优化
Tips:广义上GBDT泛指所有梯度提升树算法,包括了XGBoost。狭义上我们把GBDT定义为Gradient Boosting Decision Tree。
之后GBDT可以在参数空间和函数空间分别进行转化从梯度下降变成boosting
在参数空间中
θt=θt−1+Δθt
θt=θt−1−αtgt
其中 Δθt=−αtgt
给定初值值后,我们得
θ=∑t=0TΔθt
在函数空间中也是同理
F(x)=∑t=0Tft(x)
在XGBoost中,
唯一不同的是 Δθ=−gtHt−1
其中Boosting本身是一种加法模型
F(x)=∑t=0Tft(x)
那么我们讨论完了迭代的方法之后,我们开始讨论这两个模型的基本分类器——CART
也就是Friedman大神所创的分类和决策树,墙裂推荐他的The Elements of Statistical Learning.
那么树模型本身具有蛮多优点的:
- 可解释性强
- 可处理混合类型的特征
- 不用归一化处理
- 由特征组合的作用
- 可自然的处理缺失值
- 对异常点鲁棒性较强
- 有特征选择的作用
- 可扩展性强,容易并行
缺点是:
缺乏平滑性
不适合处理高维度稀疏的数据
接下来我们再详细的讲GBDT
本质上来说GBDT是多个CART模型的加总,给与一个适当的权重,那么我们可以设定:
F(x;w)=∑t=0Tαtht(x;wt)
其中 α 是权重,t表示每棵树的权重,w为CART的参数,h则表示CART。
之后我们把因变量放入,使用梯度下降法最小化损失函数,也就是最小化下列模型:
F∗=argminF∑i=0NL(yi,F(xi;w))
NP难问题使用贪心算法可以迭代得局部最优解
关于NP难问题之后会单开一篇进行总结
针对GBDT,我们给出了一个算法

针对这个算法,我们开始一步步进行解释:
首先我们要输入我们的自变量和应变量,基础的CART模型,和损失函数
之后给定初始化的值,开始迭代步骤
1.响应:利用损失函数的负梯度在当前模型的值,作为回归问题中提升树算法的残差的近似值
2. 学习第t棵数:估计CART拟合残差
3.线性搜索找步长:使用线性搜索使损失函数最小,类似剪枝
4.更新模型
在GBDT中,我们使用了Boosting模型,也就是加法模型,在树模型不断的叠加中,我们实际上是拟合的残差。比如第一棵CART树,之后,第二棵拟合是第一棵树和真实的应变量的差值,以此类推。
GBDT的推荐深度为6
标签:泰勒,函数,迭代,区别,梯度,XGBoost,展开式,GBDT From: https://www.cnblogs.com/Arborday/p/16908113.html