written on 2022-08-23
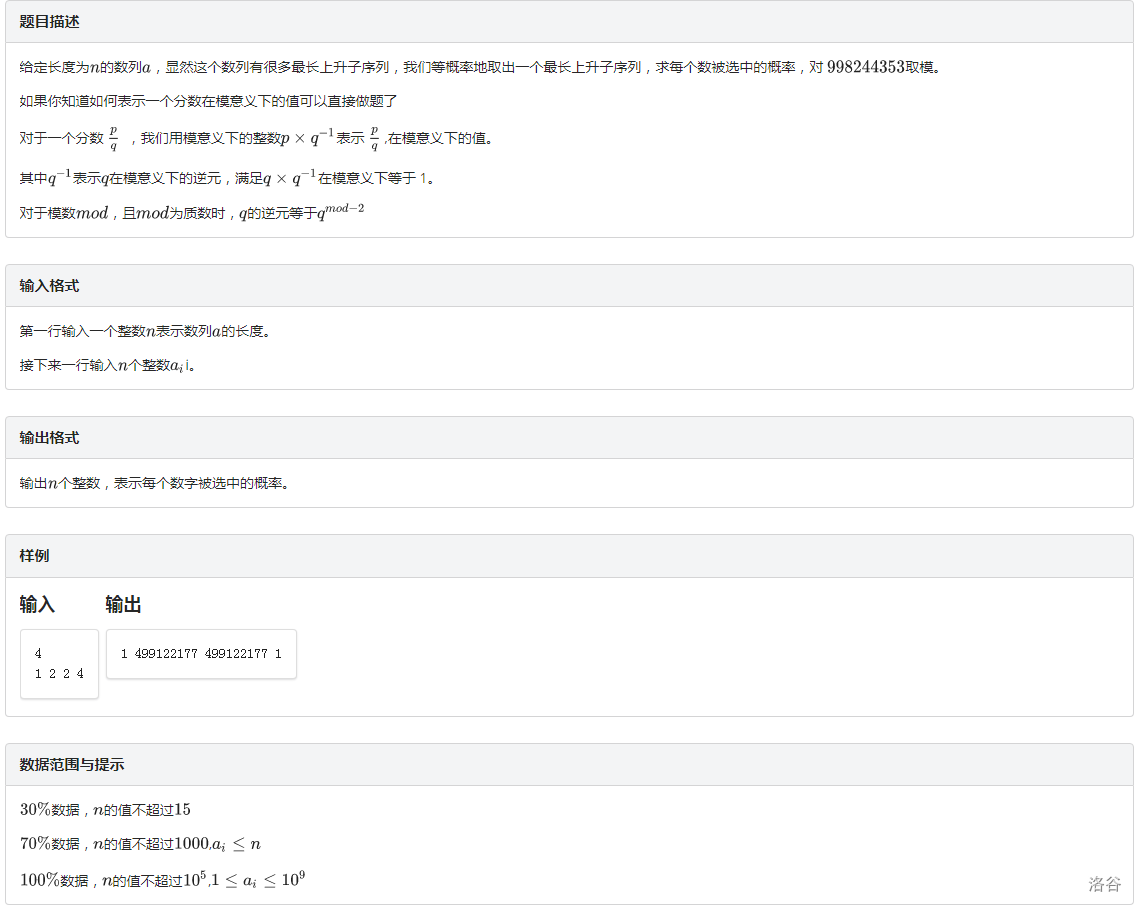
题目不是很难,考场思路偏了,很遗憾。
首先要求每个数字被选中的概率,那么根据该概率的定义我们不妨计算出总方案数以及该数出现在 LIS 中的方案数。由于数据范围较大,显然需要用树状数组或是线段树优化求解过程。(我用了线段树)
为了方便以及代码的美观性,这里最优的方式是开一个结构体重载运算符,将线段树的信息用结构体来表示,这样的话各种运算更新都和模板别无二致,代码美观调试方便。
离散化后开权值线段树,我们就能够求出 LIS 的总方案数了,那么如何计算每个数字被选中的概率呢?
考虑对于一个数字,如果他在某一个 LIS 中,那么他的左部和右部最长长度之和显然要等于 LIS 的长度。那么同理,方案数也就是左部和右部的最长长度下方案数的乘积了。为此我们从左向右做一遍最长上升子序列,从右向左做一遍最长下降子序列,即可得出答案。
具体可参考我的代码
思路很清晰,这题的启示是:判断一个数是否出现在 LIS 中,以及方案数的求法,可以用结构体封装重载运算符+线段树优化 LIS 的方法。
标签:方案,概率,线段,运算符,73,ZLOJ,LIS,最长 From: https://www.cnblogs.com/Freshair-qprt/p/16623453.html