标签：数据结构 idx int le include 节点 op

2. 数据结构（I）

2.1 链表

2.1.1 单链表

模板：AcWing 826. 单链表

题目：

实现一个单链表，实现以下 \(3\) 种操作：

H x 向链表头插入一个数 \(x\)；
D x 删除第 \(x\) 个插入的数（若 \(x=0\)，表示删除头结点）；
I k x 在第 \(k\) 个插入的数后插入一个数 \(x\)（保证 \(k>0\)）。

给你 \(m\) 次操作，输出最终链表。\(1\le m\le 10^5\)。

思路：

我们定义，\(\texttt{head}\) 指向头结点，数组 \(e\) 存储每个点的值，数组 \(ne\) 存储每个点的后继，\(idx\) 表示当前节点编号。初始时，\(\texttt{head}=-1,idx=0\)。

图2-1

如图 \(\texttt{2-1}\) 展示了一个链表。其中，\(\texttt{head}\) 指针指向头结点。然后我们来思考如何实现 \(3\) 种操作。

图2-2

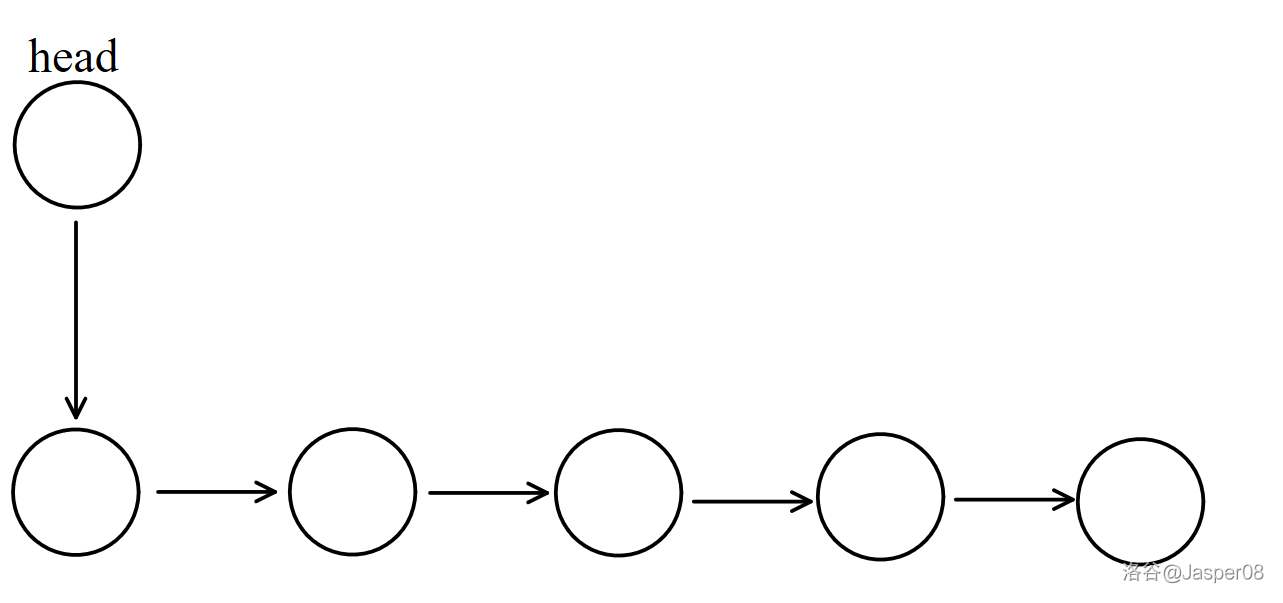
如图 \(\texttt{2-2}\) 展示了操作 H x 的方式。将 \(e_{idx}\) 设为 \(x\)，\(ne_{idx}\) 设为 \(\texttt{head}\)，然后让 \(\texttt{head}\) 指向 \(idx\)，最后 \(idx:=idx+1\)。

图2-3

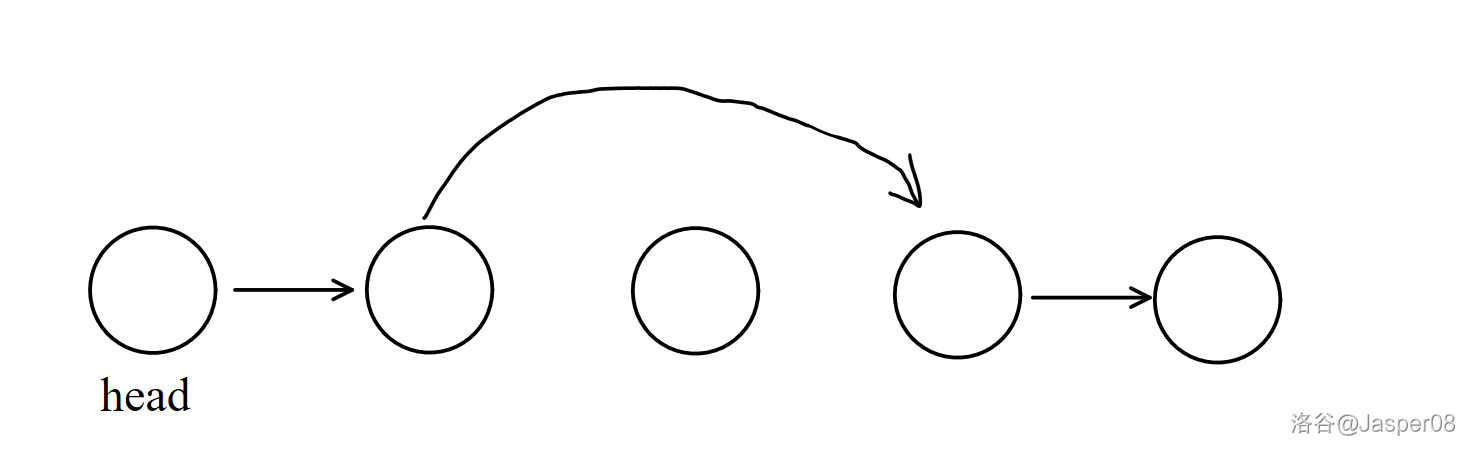
如图 \(\texttt{2-3}\) 展示了删除在 \(x\ne 0\) 时的删除操作 D x 的方式，即将 \(ne_{x-1}:=ne_{ne_{x-1}}\) 即可。

删除头结点也可以用类似的方法。

图2-4

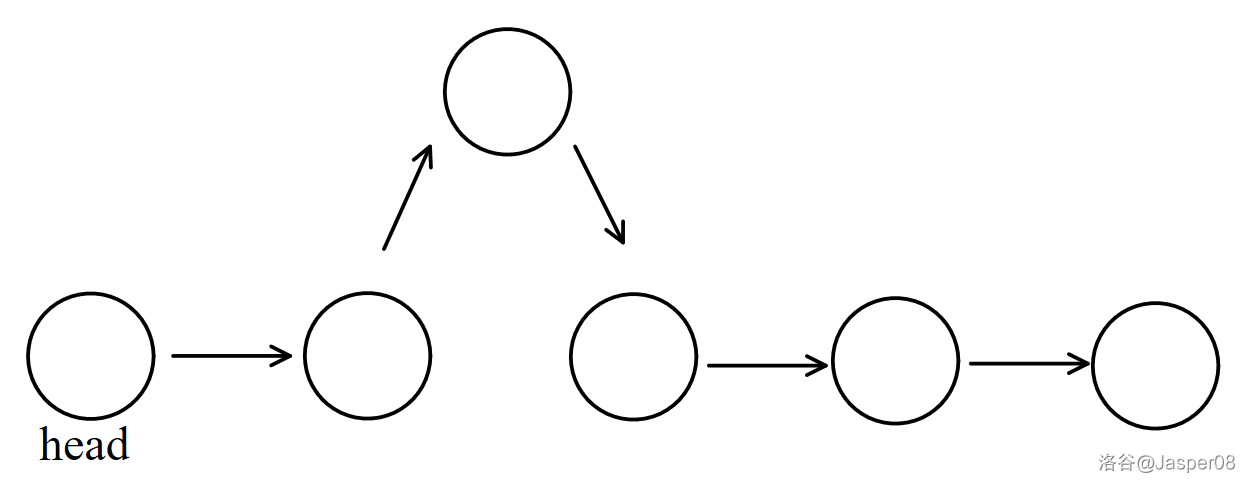
如图 \(\texttt{2-4}\) 展示了操作 I k x 的方式。即先将 \(e_{idx}\) 设为 \(x\)，\(ne_{idx}=ne_k\)，\(ne_k=idx\)，最后 \(idx:=idx+1\)。

最后输出时，从头结点开始遍历，直到 \(ne_i=-1\) 标志着链表结束。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

const int N = 1e5+10;

int m;
int e[N], ne[N], head, idx;

void add_head(int x) { //头插入(图2.2)
    e[idx] = x, ne[idx] = head, head = idx, idx ++;
}

void add(int k, int x) { //中间插入(图2.4)
    e[idx] = x, ne[idx] = ne[k], ne[k] = idx, idx ++;
}

void del_head() { //删除头结点
    head = ne[head];
}

void del(int k) { //删除中间节点(图2.3)
    ne[k] = ne[ne[k]];
}

int main() {
    scanf("%d", &m);
    
    head = -1, idx = 0; //初始化
    while (m -- ) {
        char op;
        cin >> op;
        if (op == 'H') { //头插入
            int x;
            scanf("%d", &x);
            add_head(x);
        } else if (op == 'D') { //删除节点
            int x;
            scanf("%d", &x);
            if (x == 0) del_head();
            else del(x-1); //注意删掉的是x-1而非x
        } else { //中间插入
            int k, x;
            scanf("%d%d", &k, &x);
            add(k-1, x);
        }
    }
    
    for (int i = head; i != -1; i = ne[i]) printf("%d ", e[i]);
    return 0;
}

2.1.2 双链表

模板：AcWing 827. 双链表

题目：

实现一个双链表，实现以下 \(5\) 种操作：

L x 向链表头插入一个数 \(x\)；
R x 向链表尾插入一个数 \(x\)；
D x 删除第 \(x\) 个插入的数；
IL k x 在第 \(k\) 个插入的数左侧插入一个数 \(x\)；
IR k x 在第 \(k\) 个插入的数右侧插入一个数 \(x\)。

给你 \(m\) 次操作，输出最终链表。\(1\le m\le 10^5\)。

思路：

我们定义，\(e\) 数组存储每个节点的值，\(l\) 数组存储每个节点的左侧节点，\(r\) 数组存储每个节点的右侧节点，\(idx\) 表示已使用的节点的编号。方便起见，不妨设 \(0\) 号节点为链表的头结点，\(1\) 号节点为链表的尾结点。那么显然有 \(r_0=1,l_1=0\)，初始时 \(idx=2\)。

仿照单链表，考虑插入操作 IR k x：

首先将第 \(idx\) 个节点赋值为 \(x\)。然后更新 \(idx\) 的左右节点，即 \(l_{idx}=k,r_{idx}=r_{l_{idx}}\)。再更新 \(r_{idx}\) 的左侧节点为 \(idx\)，\(l_{idx}\) 的右侧节点为 \(idx\)。

插入操作 IL k x 也可以视作在 \(l_k\) 右侧插入节点，即 IR l[k] x. L x 可以视作在 \(0\) 号节点右侧插入节点，即 IR 0 x；同理 R x 可视作在 \(1\) 号节点左侧插入节点，即 IR l[1] x.

最后考虑删除操作 D x. 显然 \(l_{r_x}:=l_x,r_{l_x}:=r_x\)。

最后从 \(r_0\) 节点开始遍历所有节点，直到遍历到 \(1\) 号节点标志着链表结束。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

const int N = 1e5+10;

int m;
int e[N], l[N], r[N], idx; 
//e数组存储每个节点的值,l数组存储每个节点左侧节点的编号,r节点存储每个节点右侧节点的编号

void add(int k, int x) {
    e[idx] = x; //将idx号点的值设为x
    l[idx] = k, r[idx] = r[k]; //更新idx的左右节点
    l[r[k]] = idx, r[k] = idx; //更新idx的左节点的右节点和右节点的左节点
    idx ++; 
}

void del(int k) {
    l[r[k]] = l[k];
    r[l[k]] = r[k];
}

int main() {
    scanf("%d", &m);
    
    r[0] = 1, l[1] = 0, idx = 2; //0表示头结点,1表示尾结点
    
    while (m -- ) {
        string op;
        cin >> op;
        if (op == "L") {
            int x;
            scanf("%d", &x);
            add(0, x); //在头节点插入
        } else if (op == "R") {
            int x;
            scanf("%d", &x);
            add(l[1], x); //在尾结点插入
        } else if (op == "D") {
            int x;
            scanf("%d", &x);
            del(x+1); //删除第x个插入的数
        } else if (op == "IR") {
            int k, x;
            scanf("%d%d", &k, &x);
            add(k+1, x); //在第k个插入的数右侧插入x
        } else {
            int k, x;
            scanf("%d%d", &k, &x);
            add(l[k+1], x); //在第k个插入的数左侧插入x,相当于在l[k]右侧插入x
        }
    }
    
    for (int i = r[0]; i != 1; i = r[i]) printf("%d ", e[i]);
    return 0;
}

2.2 栈

2.2.1 模拟栈

模板：AcWing 828. 模拟栈

题目：

实现一个栈，支持以下 \(4\) 种操作：

push x 向栈顶插入一个数 \(x\)；
pop 从栈顶弹出一个元素；
empty 判断栈是否为空；
query 查询栈顶元素。

给你 \(m\) 次操作。对于每次 empty 或 query 操作，输出对应结果。\(1\le m\le 10^5\)。

思路：

栈是一种先进后出的数据结构。

我们可以维护一个头指针 \(tt\)，指向栈顶的下一个位置（初始时 \(tt=1\)）；同时维护 \(q\) 数组表示栈。

对于每次 push 操作，将 \(x\) 的值赋给 \(q_{tt}\) 即可，然后 \(tt:=tt+1\)。

对于每次 pop 操作，将 \(tt\) 减少 \(1\) 即可。

对于每次 empty 操作，若 \(tt=1\) 说明栈空，否则栈不空。

对于每次 query 操作，输出 \(q_{tt-1}\) 即可。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

const int N = 100010;

int m;
int tt = 1; //尾指针
int q[N]; //栈

int main() {
    scanf("%d", &m);
    while (m -- ) {
        string op;
        cin >> op;
        if (op == "push") {
            int x;
            scanf("%d", &x);
            q[tt ++] = x; //向栈顶插入元素
        } 
        else if (op == "pop") tt --; //弹出栈顶元素
        else if (op == "empty") { //判断栈是否为空
            if (tt == 1) puts("YES");
            else puts("NO");
        } 
        else printf("%d\n", q[tt-1]); //输出栈顶元素
    }
    
    return 0;
}

例题：AcWing 3302. 表达式求值

题目：给你一个表达式，其中的符号只包含 +，-，*，/ 和左右括号，计算它的值。表达式的长度不超过 \(10^5\)。

思路：

开两个栈，分别存储运算数和运算符。然后扫描整个表达式：

若当前字符为数字，则提取出整个数，加入运算数栈中。
若当前字符为 (，直接加入运算符栈中。
若当前字符为 )，计算括号内表达式的值，将其结果加入运算数栈中。
若当前字符为四则运算符，将运算符栈顶的运算符与当前字符比较，若当前字符的优先级较高，则直接加入运算符栈中；否则计算之前表达式的值，再将当前字符入栈。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <stack>
#include <unordered_map>

using namespace std;

stack<int> nums;
stack<char> op;

void eval() { //计算中缀表达式的值
    int b = nums.top(); nums.pop();
    char oper = op.top(); op.pop();
    int a = nums.top(); nums.pop();
    
    int c;
    if (oper == '+') c = a + b;
    else if (oper == '-') c = a - b;
    else if (oper == '*') c = a * b;
    else c = a / b;
    
    nums.push(c);
}

int main() {
    string s;
    cin >> s;
    
    unordered_map<char, int> pr{{'+', 1}, {'-', 1}, {'*', 2}, {'/', 2}}; //每个符号的运算优先级
    for (int i = 0; i < s.size(); ++i) {
        char c = s[i];
        if (isdigit(c)) {
            int x = 0; //提取出操作数x
            while (isdigit(s[i]) && i < s.size()) {
                x = x * 10 + s[i] - '0';
                i ++;
            }
            i --;
            nums.push(x);
        }
        else if (c == '(') op.push(c);
        else if (c == ')') { //如果是右括号,从右向左计算出整个括号的值
            while (op.top() != '(' && op.size()) eval();
            op.pop();
        }
        else { //如果是运算符,那么按运算顺序计算
            while (op.size() && op.top() != '(' && pr[op.top()] >= pr[c]) eval();
            op.push(c);
        }
    }
    
    while (op.size()) eval(); //求出最终表达式的值
    cout << nums.top() << endl;
    return 0;
}

2.2.2 单调栈

例题：AcWing 830. 单调栈

题目：给你一个包含 \(n\) 个元素的数组 \(a\)，输出每个数左边比它小的第一个数，如果没有则输出 \(-1\)。 \(1\le n\le 10^5\)。

思路：

首先，我们知道一个结论：若 \(a_i>a_j\) 且 \(i<j\)，那么 \(a_i\) 对 \(a_j\) 以后的答案没有影响。证明：对于 \(a_k\;(k>j)\)，若 \(a_i<a_k\)，则 \(a_j\) 必定比 \(a_i\) 更优；若 \(a_i\ge a_k\) 则 \(a_i\) 不可能为答案。

结合上述结论，我们可以维护一个单调栈 \(\texttt{nums}\)。对于每个元素 \(a_i\)，若 \(\texttt{nums}\) 则输出 \(-1\)。否则从栈顶开始遍历每个元素，若栈顶元素大于 \(a_i\) 则将其弹出，直到栈顶元素小于 \(a_i\) （输出此时的栈顶元素）或栈为空（输出 \(-1\)）。最后将 \(a_i\) 压入栈即可。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <stack>

using namespace std;

int n;
stack<int> nums; //单调栈

int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; ++i) {
        int x;
        scanf("%d", &x);
        if (!nums.size()) printf("-1 "); //栈为空
        else {
            while (nums.size() && nums.top() >= x) nums.pop(); //找到第一个<x的元素
            if (!nums.size()) printf("-1 ");
            else printf("%d ", nums.top());
        }
        nums.push(x); //将x加入栈
    }
    return 0;
}

2.3 队列

2.3.1 模拟队列

模板：AcWing 829. 模拟队列

题目：

实现一个队列，支持以下 \(4\) 种操作：

push x 向队尾插入一个数 \(x\)；
pop 从队头弹出一个元素；
empty 判断队列是否为空；
query 查询队头元素。

给你 \(m\) 次操作。对于每次 empty 或 query 操作，输出对应结果。\(1\le m\le 10^5\)。

思路：

维护一个数组 \(q\) 和两个指针 \(hh\) 和 \(tt\)，分别指向队头和队尾。初始时 \(hh=tt=0\)。

对于 push x 操作，令 \(q_{tt}=x,tt:=tt+1\) 即可；对于 pop 操作，\(hh:=hh+1\)即可；对于 empty 操作，若 \(hh=tt\) 说明队列为空，否则说明队列不空；对于 query 操作，输出 \(q_{hh}\) 即可。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

const int N = 1e5+10;

int m;
int hh, tt; //hh指向队头,tt指向队尾
int q[N]; //模拟队列

int main() {
    scanf("%d", &m);
    while (m -- ) {
        string op;
        cin >> op;
        if (op == "push") {
            int x;
            scanf("%d", &x);
            q[tt ++] = x; //队尾插入
        } 
        else if (op == "pop") hh ++; //弹出队头
        else if (op == "empty") { //判断是否为空
            if (hh == tt) puts("YES");
            else puts("NO");
        }
        else printf("%d\n", q[hh]); //询问队头
    }
    
    return 0;
}

2.3.2 单调队列

例题：AcWing 154. 滑动窗口

题目：给定一个长度为 \(n\) 的数组和一个长度为 \(k\) 的滑动窗口。滑动窗口从数组的最左侧移动到最右侧，你需要求出每次滑动窗口内的最小值和最大值。\(1\le k\le n\le 10^6\)。

思路：

维护一个单调队列 \(q\)（其中存储的是原数组的下标），初始时，\(hh=0,tt=-1\)。这里以最小值为例，遍历整个数组，对于 \(a_i\)，若：

若队头 \(q_{hh}\le i-k\)，说明此时队头已超出窗口范围，弹出队头；
弹出队尾，直到 \(a_i>a_{q_{tt}}\)；
将 \(i\) 加入队列；
输出队头，即滑动窗口内的最小值。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

const int N = 1e6+10;

int n, k, hh, tt;
int a[N], q[N]; //q存储的是原数组下标

int main() {
    scanf("%d%d", &n, &k);
    for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
    
    hh = 0, tt = -1; //初始化队头队尾
    for (int i = 1; i <= n; ++i) {
        if (hh <= tt && q[hh] <= i-k) hh ++; //如果队头超出了滑动窗口的范围则将其弹出
        while (hh <= tt && a[q[tt]] >= a[i]) tt --; //弹出队尾直到ai能够加入队列
        q[++ tt] = i; //将t加入队列
        
        if (i >= k) printf("%d ", a[q[hh]]); //输出队头(最小值)
    }
    
    puts("");
    
    hh = 0, tt = -1; //与求最小值基本一致
    for (int i = 1; i <= n; ++i) {
        if (hh <= tt && q[hh] <= i-k) hh ++;
        while (hh <= tt && a[q[tt]] <= a[i]) tt --;
        q[++ tt] = i;
        
        if (i >= k) printf("%d ", a[q[hh]]);
    }
    
    return 0;
}`

2.4 KMP 字符串算法

模板：AcWing 831. KMP字符串

题目：给定一个长度为 \(m\) 的匹配串 \(S\) 和一个长度为 \(n\) 的模式串 \(P\)，求出 \(P\) 在 \(S\) 中所有出现位置的起始下标。\(1\le n\le 10^5,1\le m\le 10^6\)。

思路：

约定：本题中字符串的下标均从 \(1\) 开始。

首先定义 \(ne\) 数组：\(ne_{i}\) 表示 \(P[1\cdots i]\) 的最长公共前后缀的长度，且 \(ne_i<i\)。特别地，\(ne_1=0\)。

然后我们来思考如何求出 \(ne_i\)。

图2-5

如图 \(\texttt{2-5}\) 展示了 \(ne\) 数组的计算方式。设 \(ne_{i-1}=j\)，若 \(P_{j+1}=P_i\)，根据 \(ne\) 数组的定义，有 \(P[1\cdots j]=P[i-j\cdots i-1]\)，那么 \(ne_{i}=j+1\)；否则再尝试将 \(ne_j\) 与 \(i\) 进行匹配，直到无法匹配为止。

得到 \(ne\) 数组后，就可以进行 \(\texttt{KMP}\) 字符串匹配。

图2-6

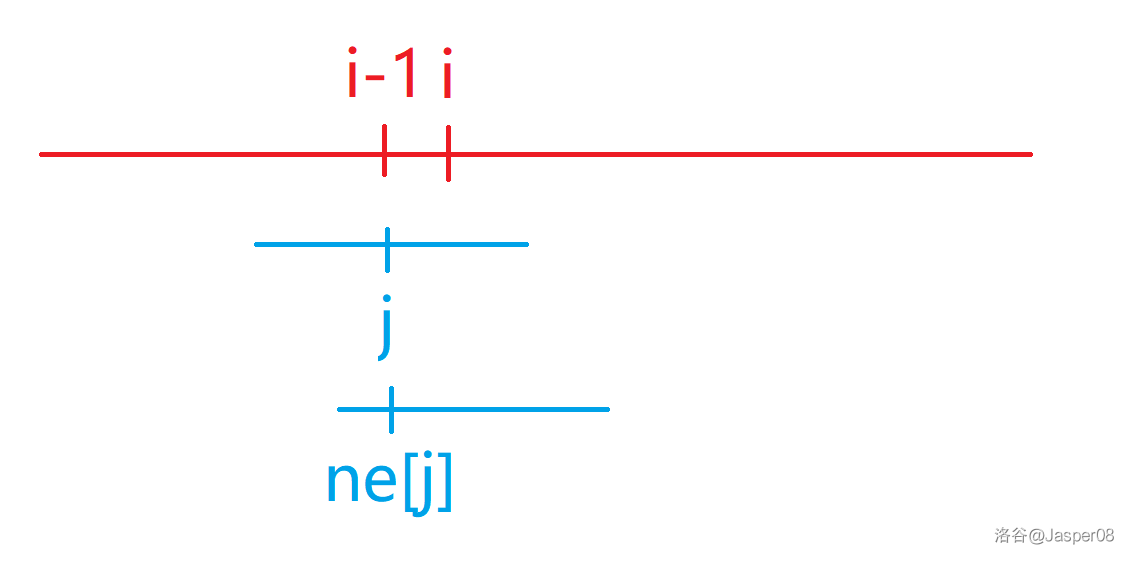
如图 \(\texttt{2.6}\) 展示了 \(\texttt{KMP}\) 字符串匹配的方式。假设 \(S[i-j\cdots i-1]\) 和 \(P[1\cdots j]\) 已经匹配，若 \(S_i=P_{j+1}\) 则继续匹配；否则 \(j=ne_j\)，继续尝试匹配。若全部匹配成功，输出 \(i-n\) 即可。

时间复杂度 \(O(n+m)\)。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

const int N = 1e5+10, M = 1e6+10;

int n, m;
char p[N], s[M]; //模式串和匹配串
int ne[N]; //ne[i]存储p中第i个字符的最长公共前后缀长度

int main() {
    cin >> n >> p+1 >> m >> s+1;
    
    ne[1] = 0;
    for (int i = 2, j = 0; i <= n; ++i) { //求出ne数组
        while (j && p[i] != p[j+1]) j = ne[j];
        if (p[i] == p[j+1]) j ++;
        ne[i] = j;
    }
    
    for (int i = 1, j = 0; i <= m; ++i) { //kmp 字符串匹配
        while (j && s[i] != p[j+1]) j = ne[j];
        if (s[i] == p[j+1]) j ++;
        if (j == n) {
            printf("%d ", i-n);
            j = ne[j];
        }
    }
    
    return 0;
}

2.5 Trie 树

2.5.1 字典 Trie

模板：AcWing 835. Trie字符串统计

题目：

维护一个字符串集合，支持两种操作：

I s 插入一个字符串 \(s\)；
Q s 询问字符串 \(s\) 出现的次数。

给你 \(n\) 次操作。\(1\le n\le 2\times 10^4,1\le \text{len}(s)\le 10^5\) 且 \(s\) 中只包含小写字母（\(\text{len}(s)\) 表示 \(s\) 的长度）。

思路：

维护一棵 \(\texttt{Trie}\) 树（字典树）。

如果现在有 \(8\) 个字符串：\(\texttt{abcd,aacd,aabc,aabc,acd,bb,bbc,cdab}\)，那么它们所构成的 \(\texttt{Trie}\) 树如图 \(\texttt{2.7}\)：

图2-7

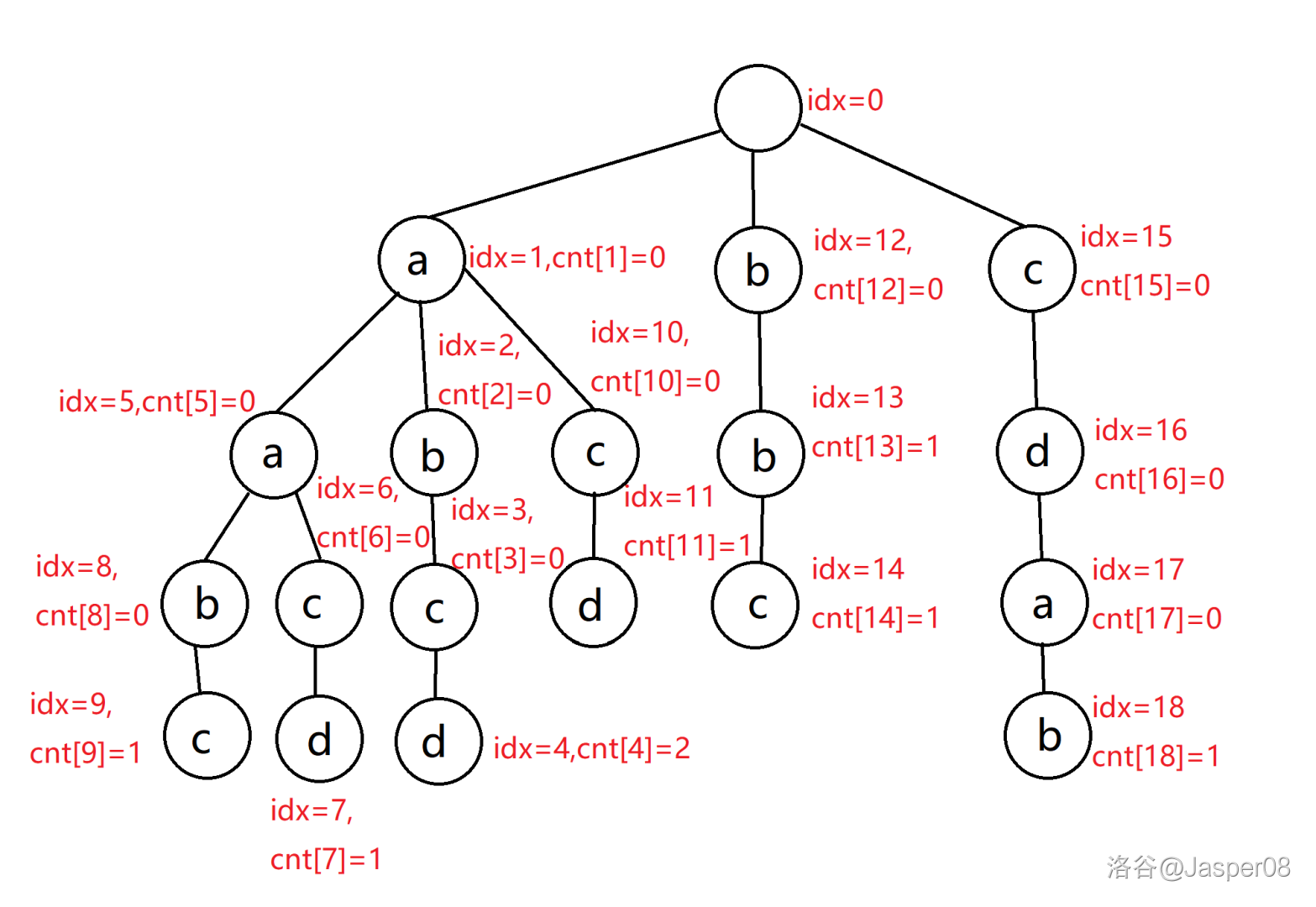
其中，\(idx\) 表示每个节点的编号，\(cnt_i\) 表示以第 \(i\) 个节点为结尾的字符串的数量。另外我们还需要维护一个数组 \(son\)，\(son_{i,j}\) 存储 \(i\) 号节点的第 \(j\) 个儿子的编号。

对于每次插入操作，从根节点开始遍历，若某个节点不存在则将其加入 \(\texttt{Trie}\) 树。对于每次查找操作，从根节点开始遍历，若某个节点不存在则直接返回 \(0\)。

时间复杂度 \(O(n\log n)\)。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

const int N = 1e5+10;

int n;
int son[N][26], cnt[N], idx; //son存储节点编号,cnt存储每个节点的数量
//0号节点既是根节点,也是空节点

void insert(string s) { //插入一个字符串s
    int p = 0; //从根节点开始遍历
    for (int i = 0; i < s.size(); ++i) {
        int u = s[i] - 'a';
        if (!son[p][u]) son[p][u] = ++ idx; //如果该节点不存在,则插入新节点
        p = son[p][u];
    }
    cnt[p] ++;
}

int query(string s) { //查询s出现的次数
    int p = 0;
    for (int i = 0; i < s.size(); ++i) {
        int u = s[i] - 'a';
        if (!son[p][u]) return 0; //如果该节点不存在,直接返回0
        p = son[p][u];
    }
    return cnt[p]; 
}

int main() {
    scanf("%d", &n);
    while (n -- ) {
        char op; string s;
        cin >> op >> s;
        if (op == 'I') insert(s);
        else cout << query(s) << endl;
    }
    return 0;
}

2.5.2 01 Trie

例题：AcWing 143. 最大异或对

题目：给你 \(n\) 个整数 \(a_1,a_2,a_3,\cdots,a_n\)，找出一个数对 \((i,j)\)，使得 \(a_i\oplus a_j\) 最大。\(1\le n\le 10^5,0\le a_i\le 2^{31}\)。

思路;

异或运算 \(\oplus\) 相当于不进位的加法。我们可以构建一棵由 \(0\) 和 \(1\) 构成的 \(\texttt{Trie}\) 树，对于每个数 \(a_i\)，遍历 \(\texttt{01 Trie}\) 树找到与其异或的最大值即可。

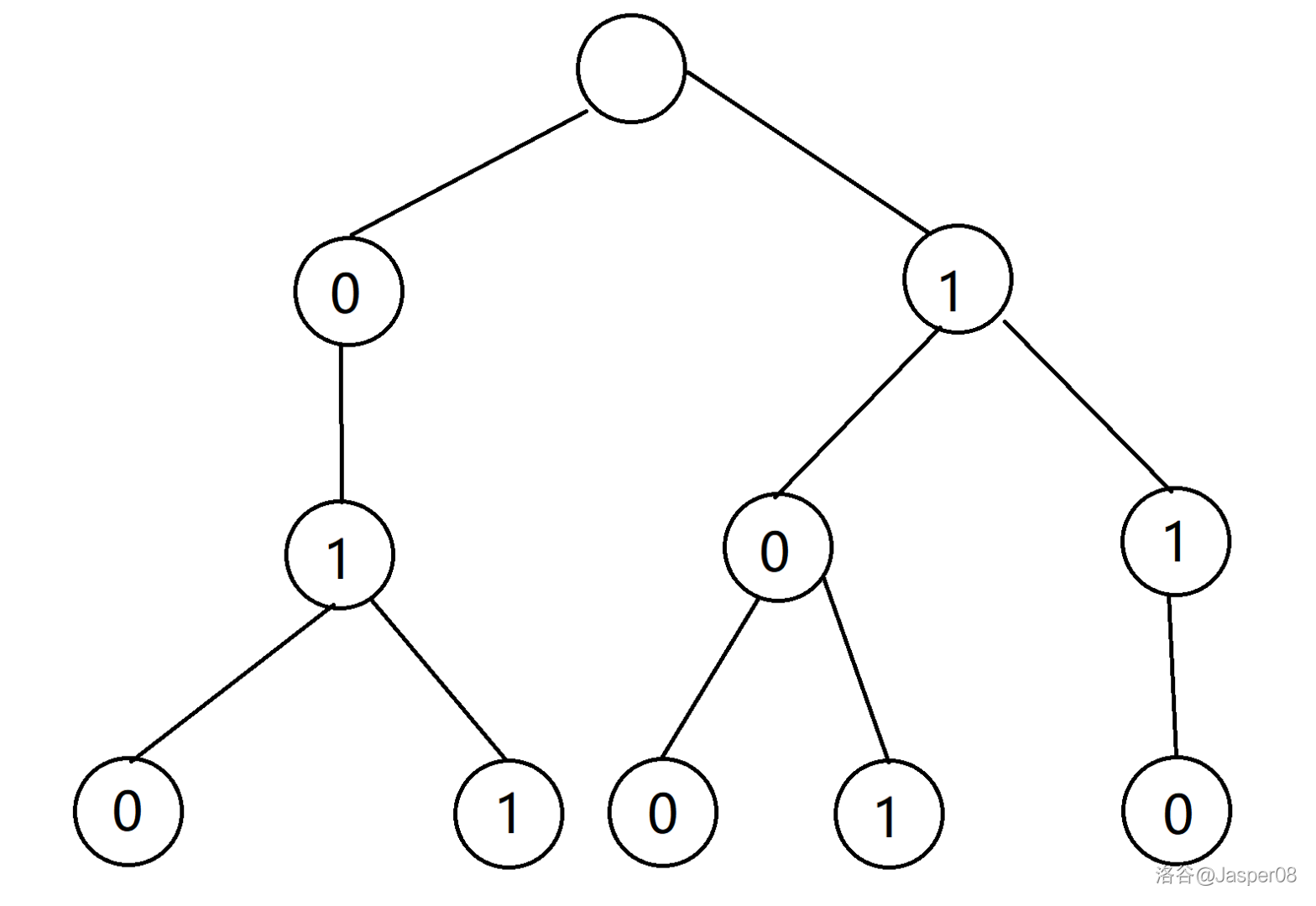
例如，对于数组 \(a=[2,3,4,5,6]\)，由将其全部由二进制表示并插入 \(\texttt{01 Trie}\) 树，可得：

图2-8

以数 \(4\) 为例，演示通过 \(\texttt{01 Trie}\) 找到与 \(4\) 异或后的最大值：

图2-9

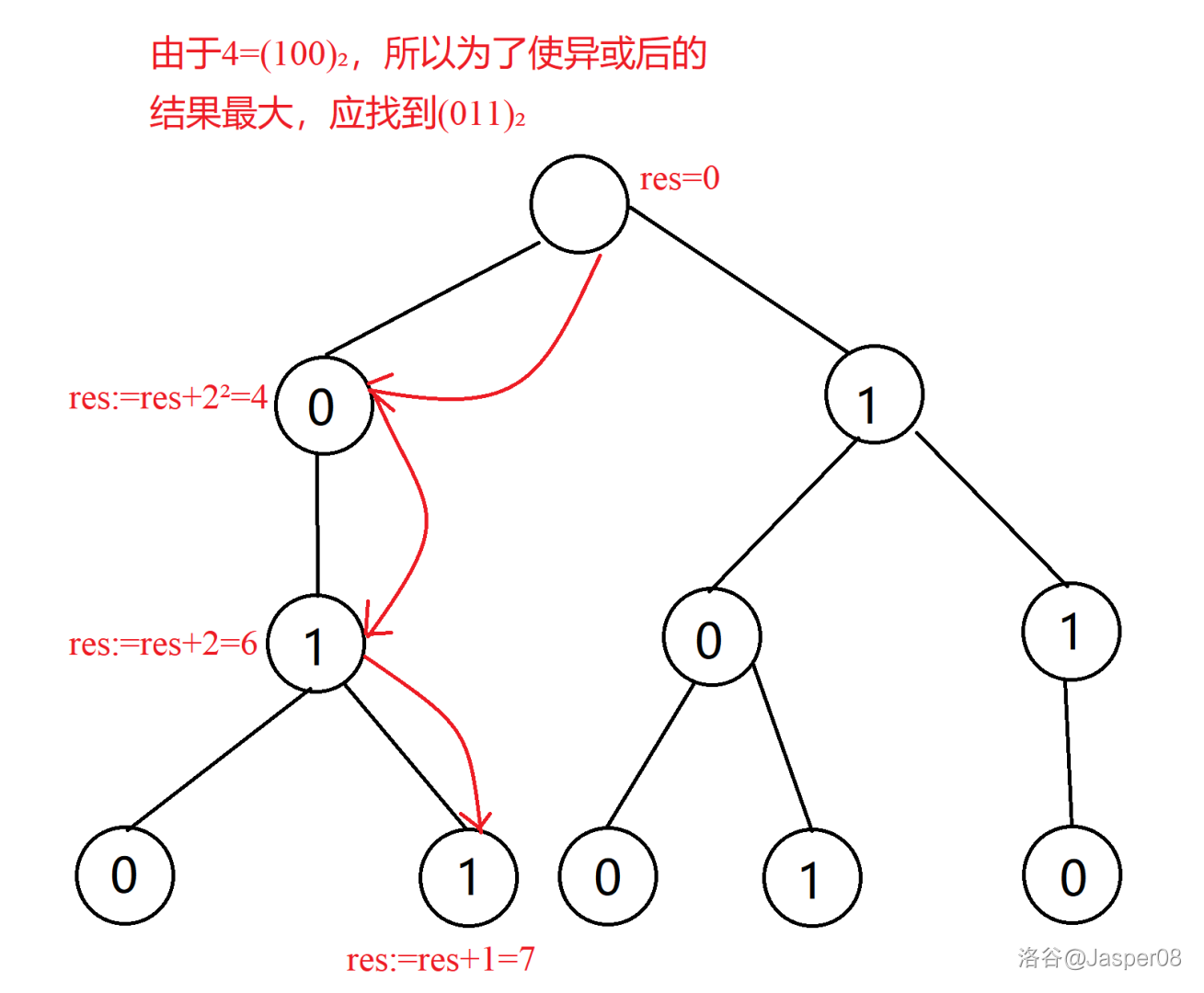
如图 \(\texttt{2.9}\)，\(4\) 异或后的最大值为 \(7\)。那么如果找不到某一个数怎么办呢？以数 \(6\) 为例，演示通过 \(\texttt{01 Trie}\) 找到与 \(6\) 异或后的最大值：

图2-10

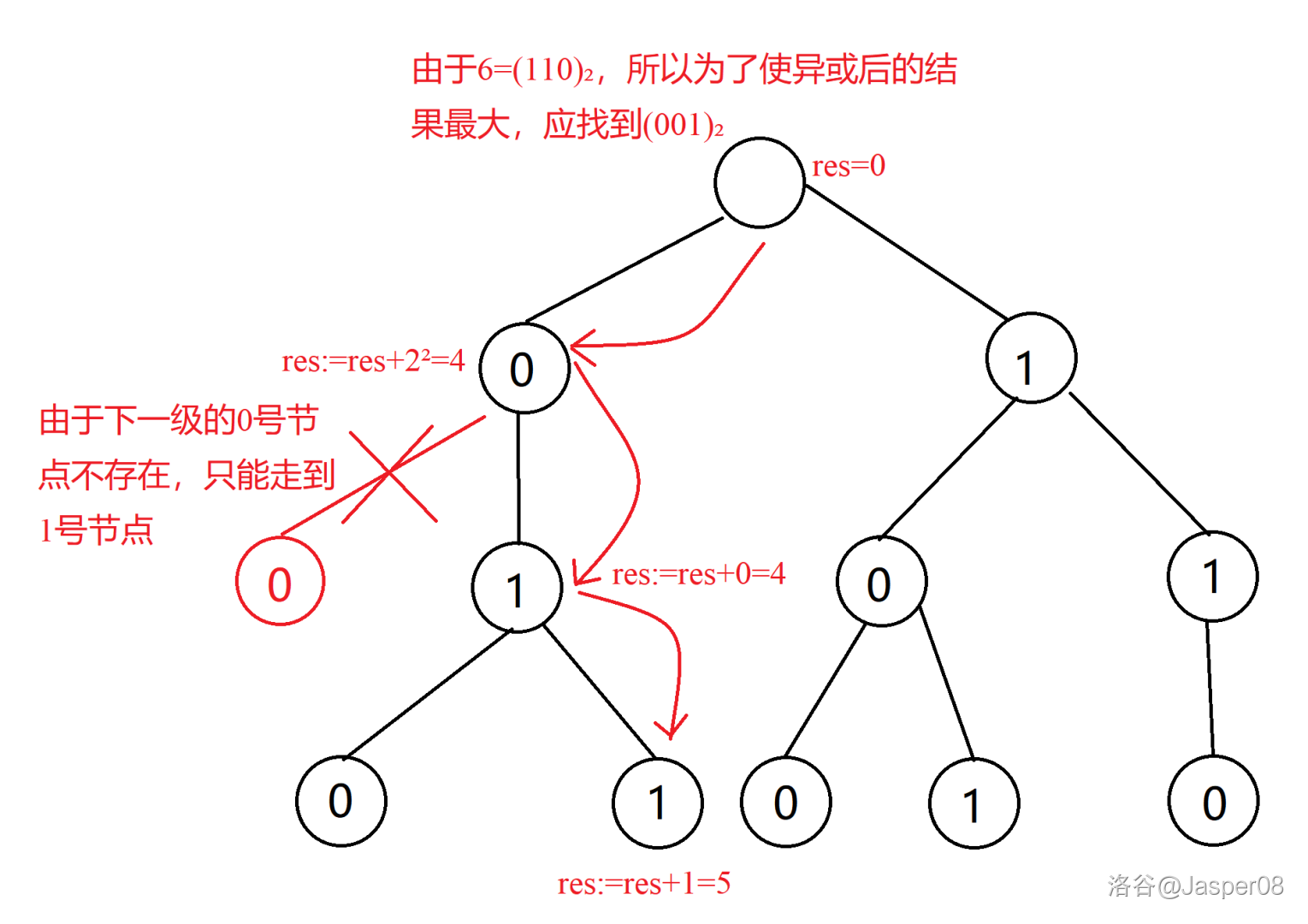
如图 \(\texttt{2-10}\)，\(6\) 异或后的最大结果为 \(5\)。

通过 \(\texttt{01 Trie}\)，可以将暴力 \(O(n^2)\) 的复杂度降至约 \(O(10^5\times 31)=O(3\times 10^6)\)。

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

const int N = 1e5+10, M = 3e6+10;

int n, a[N];
int son[M][2], idx; //son存储子节点

void insert(int x) { //将一个数x插入01Trie
    int p = 0;
    for (int i = 30; i >= 0; --i) {
        int s = x >> i & 1;
        if (!son[p][s]) son[p][s] = ++ idx; //如果子节点不存在,则创建新节点
        p = son[p][s];
    }
}

int query(int x) { //查询x的最大异或结果
    int p = 0, res = 0;
    for (int i = 30; i >= 0; --i) {
        int s = x >> i & 1; //存储x的二进制表示的倒数第i+1位的数
        if (son[p][!s]) res += 1 << i, p = son[p][!s]; 
        else p = son[p][s];
    }
    return res;
}

int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; ++i) {
        scanf("%d", &a[i]);
        insert(a[i]);
    }
    
    int maxl = 0;
    for (int i = 1; i <= n; ++i) maxl = max(maxl, query(a[i]));
    printf("%d\n", maxl);
    return 0;
}

2.6 并查集

模板：AcWing 836. 合并集合

题目：

初始时一共有 \(n\) 个数 \(1\sim n\)，每个数都在各自的集合中。给你 \(m\) 次操作：

M a b 表示将数 \(a\) 所在的集合和数 \(b\) 所在的集合合并；
Q a b 表示询问数 \(a\) 和数 \(b\) 是否在一个集合中。

\(1\le n,m\le 10^5\)。

思路：

并查集的思想是将每个集合视作一棵树，那么所有集合就可以视作一个森林。定义一个数组 \(p\)，存储每个数的父亲。初始时，所有节点的父亲都是自己，即 \(p_i=i\)。另外我们定义一个函数 \(find(x)\)，表示寻找 \(x\) 的祖宗节点。

对于 M 操作，我们可以令 \(p_{find(a)}=find(b)\)，即将 \(a\) 的祖宗的父亲设为 \(b\) 的祖宗；对于 Q 操作，若 \(find(a)=find(b)\) ，即 \(a\) 的祖先和 \(b\) 的祖先相同，则说明数 \(a\) 和数 \(b\) 在同一个集合中。

在并查集的 \(find(x)\) 函数中，我们可以使用“路径压缩”的方式来加快速度。即将 \(x\) 的祖宗设为 \(x\) 的父亲，同时将查找路径上的所有点的父亲都设为 \(x\) 的祖宗。

时间复杂度 \(O(n\log n)\)。若增加“按秩合并”优化，可使时间复杂度进一步降低至 \(O(n\alpha(n))\)，其中 \(\alpha(n)\) 为反阿克曼函数。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

const int N = 1e5+10;

int n, m;
int p[N];

int find(int x) { //查找x的祖先
    if (p[x] != x) p[x] = find(p[x]); //路径压缩
    return p[x];
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++i) p[i] = i;
    
    char op; int a, b;
    while (m -- ) {
        cin >> op >> a >> b;
        if (op == 'M') p[find(a)] = find(b);
        else (find(a) == find(b)) ? puts("Yes") : puts("No");
    }
    
    return 0;
}

例题：AcWing 837. 连通块中点的数量

题目：

初始时，给你一个包含 \(n\) 个点的图（无边）和 \(m\) 次操作：

C a b 表示在 \(a\) 和 \(b\) 之间连一条无向边；
Q1 a b 表示询问 \(a\) 和 \(b\) 是否位于一个连通块内；
Q2 a 表示询问 \(a\) 所在的连通块的大小。

\(1\le n,m\le 10^5\)。

思路：

除了维护一个 \(p\) 数组存储每个节点的父亲节点，我们还需要维护一个 \(s\) 数组来存储每个连通块的大小。注意，\(s_i\) 当且仅当 \(i\) 为祖宗节点时才有意义，表示以 \(i\) 为祖宗节点的连通块的大小。

合并时，若 \(a\ne b\)，先将两个连通块的大小相加，即 \(s_{find(b)}:=s_{find(b)}+s_{find(a)}\)，然后再 \(p_{find(a)}:=find(b)\)。其他与并查集完全相同。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

const int N = 1e5+10;

int n, m;
int p[N], s[N]; //s存储每个集合内的连通块数量(只在下标为祖宗节点时有意义)

int find(int x) { //并查集
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main() {
    scanf("%d%d", &n, &m);
    
    for (int i = 1; i <= n; ++i) p[i] = i, s[i] = 1;
    
    while (m -- ) {
        string op; 
        cin >> op;
        if (op == "C") { //合并集合
            int a, b;
            cin >> a >> b;
            if (find(a) != find(b)) s[find(b)] += s[find(a)], p[find(a)] = find(b); //要先加上数量再合并
            //注意,只需要当a,b在不同联通块时才能进行合并,否则会导致一个连通块内点的数量翻倍
        } else if (op == "Q1") { //查询是否位于同一个连通块内
            int a, b;
            cin >> a >> b;
            (find(a) == find(b)) ? puts("Yes") : puts("No");
        } else { //查询连通块内点的数量
            int a;
            cin >> a;
            printf("%d\n", s[find(a)]);
        }
    }
    return 0;
}

例题：AcWing 240. 食物链

题目：

有 \(3\) 种动物 \(A,B,C\)，\(A\) 吃 \(B\)，\(B\) 吃 \(C\)，\(C\) 吃 \(A\)。有 \(N\) 种动物，从 \(1\sim N\) 编号，每个动物都是 \(A,B,C\) 中的一种。

有人用 \(2\) 种说法对这 \(N\) 种动物进行描述：

1 X Y 表示 \(X\) 和 \(Y\) 是同类。
2 X Y 表示 \(X\) 吃 \(Y\)。

此人对 \(N\) 个动物一句接一句地说了 \(K\) 句话，其中有真话也有假话。

当一句话满足下列三个条件之一时，这句话就是假话，否则就是真话：

当前的话与前面的某些真话冲突，就是假话；
当前的话中 \(X>N\) 或 \(Y>N\)，就是假话；
当前的话表示 \(X\) 吃 \(X\)，就是假话。

根据给定的 \(N\) 和 \(K\) 句话，输出假话的总数。\(1\le N\le 5\cdot 10^4.1\le K\le 10^5\)。

思路：

我们可以使用“带边权并查集”，令 \(d_i\) 表示 \(i\) 号节点到父节点的距离。

那么我们可以根据 \(d_i\) 除以 \(3\) 的余数将动物分为 \(3\) 类：

\(d_i \equiv 0\pmod 3\)
\(d_i\equiv 1\pmod 3\)
\(d_i\equiv 2\pmod 3\)

对于 1 X Y（\(X,Y\) 为同类），可以看出，若 \(x\) 号节点和 \(y\) 号节点在同一棵树上，且 \(d_x-d_y\equiv 0\pmod 3\)，说明 \(x,y\) 为同一种动物，即这句话是真话；若 \(x\) 号节点和 \(y\) 号节点不在同一棵树上，说明这两种动物之前还没有产生联系，则这句话为真话，设 \(px=find(x),py=find(y)\)，可以令 \(p_{px}=py,d_{px}=d_y-d_x\)。

对于 2 X Y（\(X\) 吃 \(Y\)），可以看出，若 \(x\) 号节点和 \(y\) 号节点在同一棵树上，且 \(d_x-d_y+1\equiv 0\pmod 3\)，说明 \(x\) 吃 \(y\)，即这句话是真话；若 \(x\) 号节点和 \(y\) 号节点不在同一棵树上，说明这两种动物之前还没有产生联系，则这句话为真话，设 \(px=find(x),py=find(y)\)，可以令 \(p_{px}=py,d_{px}=d_y-d_x-1\)。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

const int N = 50010;

int n, k, cnt;
int p[N], d[N]; //带边权并查集

int find(int x) {
    if (p[x] != x) {
        int tmp = find(p[x]); //递归更新p[x]到根节点的距离(路径压缩后,p[x]的父亲节点即为其祖宗节点)
        d[x] += d[p[x]]; //x到根节点(路径压缩后的根节点)的距离=x到p[x]的距离(即d[x])+p[x]到其父节点(即根节点)的距离
        p[x] = tmp; //路径压缩
    }
    return p[x];
}

int main() {
    scanf("%d%d", &n, &k);
    for (int i = 1; i <= n; ++i) p[i] = i; //初始时,每个点的父亲是自己,到自己的距离为0
    
    int op, x, y;
    while (k -- ) {
        scanf("%d%d%d", &op, &x, &y);
        if (x > n || y > n) {cnt ++; continue;} //x>n,y>n是假话
        
        int px = find(x), py = find(y);
        if (op == 1) {
            if (px == py) { //在同一棵树上
                //(d[x]-d[y]) % 3 = 0说明是真话,否则是假话
                if ((d[x]-d[y]) % 3)
                    cnt ++;
            } else { //不在同一棵树上,说明x,y之前没有联系,视作真话
                d[px] = d[y] - d[x];
                p[px] = py;
            }
        } else {
            if (px == py) {
                if ((d[x]-d[y]+1) % 3)
                    cnt ++;
            } else {
                d[px] = d[y] - d[x] - 1;
                p[px] = py;
            }
        }
    }
    printf("%d\n", cnt);
    return 0;
}

2.7 堆

例题：AcWing 838. 堆排序

题目：

给你一个长度为 \(n\) 的数组 \(a\)，输出前 \(m\) 小的数。\(1\le m\le n\le 10^5,1\le a_i\le 10^9\)。

思路：

堆可以看作是一个完全二叉树，所以我们可以用存储二叉树的方式来存储它，若下标为 \(n\) 的点为一个父亲节点，则其左儿子的下标为 \(2n\)，右儿子的下标为 \(2n+1\)。在本题中我们使用的是小根堆，对于每一个父亲节点 \(u\)，它存储的值小于等于它的左儿子或右儿子，即\(a_u\le\min(a_{2u},a_{2u+1})\)。

下图（\(\texttt{2-11}\)）展示了一个小根堆：

图2-11

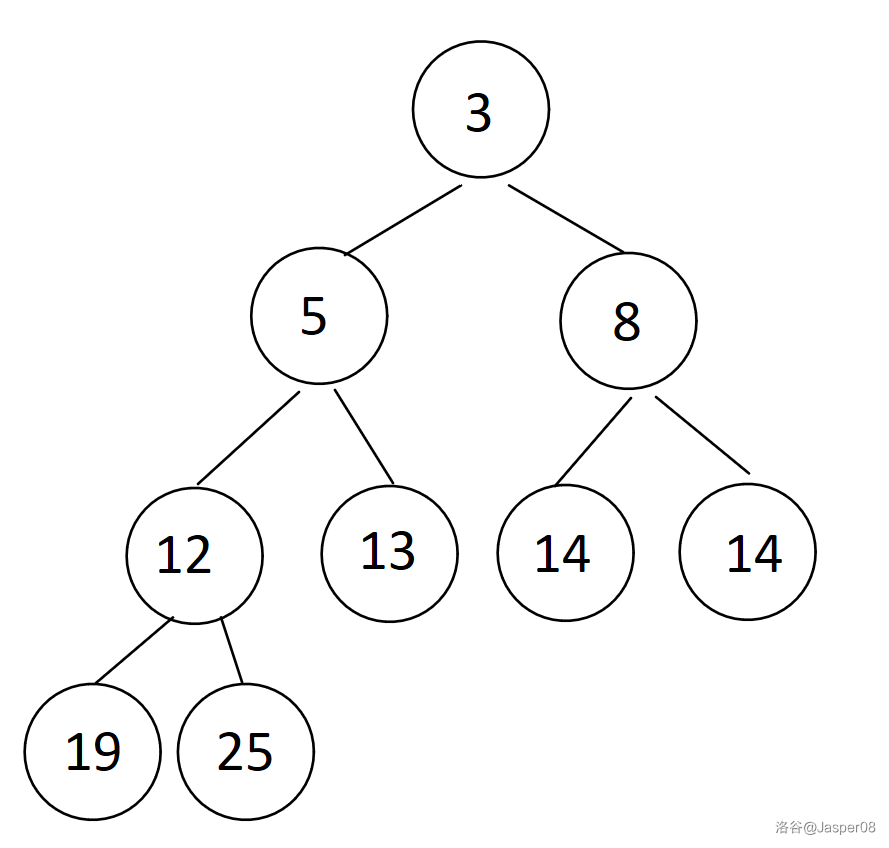
堆有两个个关键的操作——down 操作和 up 操作，时间复杂度均为 \(O(\log n)\)。对于一个左右子树均为堆的非叶子节点 \(u\) ，down(u) 意味着将 \(u\) 下传至堆中合适的位置，使其满足堆的性质。对于一个节点 \(u\)，up(u) 意味着将 \(u\) 上传至堆中合适的位置，使其满足堆的性质。在本题中我们只需要用到 down 操作。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

const int N = 1e5+10;

int n, m;
int a[N], s;

void down(int u) { //时间复杂度O(log n)
    int t = u;
    //u*2和u*2+1分别是u的左儿子和右儿子
    if (u*2 <= s && a[u*2] < a[t])
        t = u*2;
    if (u*2+1 <= s && a[u*2+1] < a[t]) 
        t = u*2+1; //若a[u]>min(a[2u],a[2u+1]),则在左儿子和右儿子中取较小值与a[u]交换
    if (t != u) {
        swap(a[t], a[u]);
        down(t);
    }
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
    s = n;
    
    for (int i = n/2; i > 0; --i) down(i);
    //从n/2开始倒序建堆，是因为n/2+1,...,n均为叶子结点,不需要down操作
    for (int i = 1; i <= m; ++i) {
        printf("%d ", a[1]);
        a[1] = a[s], s --; //每次取出堆头后将堆头删去,用最后一个元素替代它
        down(1); //下传堆头元素
    }
    return 0;
}

模板：AcWing 839. 模拟堆

题目：

维护一个集合，初始时集合为空，支持如下几种操作：

I x，插入一个数 \(x\)；
PM，输出当前集合中的最小值；
DM，删除当前集合中的最小值（数据保证此时的最小值唯一）；
D k，删除第 \(k\) 个插入的数；
C k x，修改第 \(k\) 个插入的数，将其变为 \(x\)；

现在要进行 \(N\) 次操作，对于所有 PM 操作，输出当前集合的最小值。\(1\le N\le 10^5,-10^9\le x\le 10^9\)。

思路：

本题中的 \(5\) 个操作均可以用堆的 down 和 up 操作来实现。下面为 up 操作的实现方式：

void up(int u) {
    while (u / 2 > 0 && h[u] < h[u/2]) {
        //如果u存在父节点且u节点上的值比其父节点上的值要小.则交换这两个点
        swap(u, u/2); 
        u /= 2;
    }
}

本题的难点在于如何实现后两个操作。我们可以仿照链表的存储方式，用变量 \(m\) 来存储当前插入节点的编号。另外我们维护两个数组 \(ph\) 和 \(hp\)，\(ph_i\) 表示堆中 \(i\) 号节点所对应的插入编号，\(hp_i\) 表示插入编号 \(i\) 在堆中所对应的节点序号。与上一道例题一样，我们还需要一个变量 \(s\) 来存储堆的大小，一个数组 \(h\) 来存储堆中的元素。

由于增加了数组 \(ph\) 和 \(hp\)，堆中元素的交换变的更加复杂。所以我们可以写一个函数 heap_swap 来处理堆中两个编号为 \(a,b\) 的元素的交换。

void heap_swap(int a, int b) { //将堆中编号为a,b的两个点互换
    swap(ph[hp[a]], ph[hp[b]]); //交换节点编号
    swap(hp[a], hp[b]); //交换插入编号
    swap(h[a], h[b]);
}

down 操作和 up 操作中的 swap 也需要替换成 heap_swap.

void down(int u) {
    int t = u;
    if (u*2 <= s && h[u*2] < h[t]) t = u*2;
    if (u*2+1 <= s && h[u*2+1] < h[t]) t = u*2+1;
    if (t != u) {
        heap_swap(t, u);
        down(t);
    }
} 

void up(int u) {
    while (u / 2 > 0 && h[u] < h[u/2]) {
        heap_swap(u, u/2);
        u /= 2;
    }
}

有了这三个核心操作，我们就可以完成题目所给的要求了。

I x：插入一个数 \(x\)。堆的大小 \(s\) 和插入序号 \(m\) 都需要增加 \(1\)；此时 \(ph_s=m,hp_m=s,h_s=x\)。然后再将 \(s\) 号节点 up 操作即可。
PM：输出堆中的最小元素。由小根堆的性质，直接输出 \(h_1\) 即可。
DM：删除堆中的最小元素。将 \(1\) 号节点和 \(s\) 号节点交换，\(s\) 再减去 \(1\)（删除一个元素，大小减少 \(1\)），再将 \(1\) 号节点 down 操作即可。
D k：删除插入序号为 \(k\) 的节点。插入序号为 \(k\) 的节点在堆中的序号为 \(ph_k\)，仿照 DM 操作，将 \(s\) 号节点和 \(ph_k\) 号节点交换，\(s\) 减去 \(1\)，再将 \(ph_k\) 号节点分别 down 和 up 操作一次即可。
C k x：将插入序号为 \(k\) 的节点的值更改为 \(x\)。仿照 D k 操作，将 \(h_{ph_k}\) 设为 \(x\)，再将 ph_k 号节点分别 down 和 up 操作一次即可。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

const int N = 1e5+10;

int n, m, s;
int h[N], ph[N], hp[N];

void heap_swap(int a, int b) { 
    swap(ph[hp[a]], ph[hp[b]]); 
    swap(hp[a], hp[b]); 
    swap(h[a], h[b]);
}

void down(int u) {
    int t = u;
    if (u*2 <= s && h[u*2] < h[t]) t = u*2;
    if (u*2+1 <= s && h[u*2+1] < h[t]) t = u*2+1;
    if (t != u) {
        heap_swap(t, u);
        down(t);
    }
} 

void up(int u) {
    while (u / 2 > 0 && h[u] < h[u/2]) {
        heap_swap(u, u/2);
        u /= 2;
    }
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0), cout.tie(0);

    cin >> n;
    while (n -- ) {
        string op; 
        cin >> op;
        if (op == "I") {
            int x; cin >> x;
            s ++, m ++;
            ph[m] = s, hp[s] = m;
            h[s] = x; up(s);
        } else if (op == "PM") {
            cout << h[1] << endl;
        } else if (op == "DM") {
            heap_swap(1, s);
            s --;
            down(1);
        } else if (op == "D") {
            int k; cin >> k;
            k = ph[k];
            heap_swap(k, s);
            s --;
            down(k), up(k);
        } else {
            int k, x; cin >> k >> x;
            k = ph[k];
            h[k] = x;
            down(k), up(k);
        }
    }
    return 0;
}

2.8 哈希表

2.8.1 普通哈希

模板：Acwing 840. 模拟散列表

题目：

维护一个集合，支持以下两种操作：

I x 插入一个数 \(x\)；
Q x 询问 \(x\) 是否在集合中出现过。

给定 \(n\) 次操作，对于每次 Q x 操作输出对应结果 Yes 或 No.

\(1\le N\le 10^5,-10^9\le x\le 10^9\)。

思路：

哈希有两种实现方式：拉链法和开放寻址法。其本质都是通过一个哈希函数 \(f(x)\) 来实现将较大范围的数（或负数）映射到一个较小的区间 \([0,k)\) 内，以实现快速查找。但由于不同的数可能映射到一个相同的值，所以我们需要一些方法来进行处理。

拉链法：对于区间 \([0,k)\) 中的每一个数，开一个链表存储其映射到的数（即邻接表），每次遍历查找即可。

开放寻址法：若当前 \(f(x)\) 的位置上已经存了一个数，则向后（若到了尾部则跳到 \(0\)）不断查找第一个没有存数的点并将其插入。

代码：

拉链法：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 1e5+10;
const int p = 100003;

int n;

int h[N], e[N], ne[N], idx;

int f(int x) {
    return (long long)x * x % p;
}

void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}

void insert(int x) {
    int x_ = f(x);
    add(x_, x);
}

bool check(int x) {
    int x_ = f(x);
    for (int i = h[x_]; i != -1; i = ne[i]) {
        int j = e[i];
        if (j == x) return 1;
    }
    return 0;
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0), cout.tie(0);
    
    cin >> n;
    memset(h, -1, sizeof h);
    char op; int x;
    while (n -- ) {
        cin >> op >> x;
        if (op == 'I') insert(x);
        else {
            if (check(x)) puts("Yes");
            else puts("No");
        }
    }
    
    return 0;
}

开放寻址法：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 1e6+10;
const int p = 999987;

int n;

int h[N];

int f(int x) {
    return (x % p + p) % p;
}

int find(int x) {
    int x_ = f(x);
    while (h[x_] != 0x3f3f3f3f && h[x_] != x) {
        x_ ++;
        if (x_ > p) x_ = 0;
    }
    return x_;
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0), cout.tie(0);
    
    cin >> n;
    memset(h, 0x3f, sizeof h);
    char op; int x;
    while (n -- ) {
        cin >> op >> x;
        if (op == 'I') h[find(x)] = x;
        else {
            if (h[find(x)] != 0x3f3f3f3f) puts("Yes");
            else puts("No");
        }
    }
    
    return 0;
}

2.8.2 字符串哈希

模板：Acwing841. 字符串哈希

题目：给定一个长度为 \(n\) 的字符串 \(s\) 和 \(m\) 次询问，每次询问给定两个区间 \([l_1, r_1],[l_2,r_2]\)，判断这两个区间所包含的子串是否完全相同。

\(s\) 中只包含大小写字母及数字，且位置从 \(1\) 开始编号，\(1\le n,m\le 10^5\)。

思路：

对于字符串，我们有一种常用的哈希方式。将该字符串视作一个 \(p\) 进制数，将其转换为十进制后对 \(q\) 取模。通常取 \(p=131\) 或 \(13331\)，\(q=2^{64}\)（可直接通过 unsigned long long 的溢出取模）。

我们可以先计算 \(s\) 中所有前缀字符串的的哈希值。定义 \(h_i\) 表示 \(s\) 中 \([1,s]\) 之间字符的哈希值。显然 \(h_0=0\)，那么 \(h_i=h_{i-1}\times p+s_i\)。

接下来，我们可以通过 \(h\) 求出每个子串的哈希值。对于区间 \([l,r]\)，其包含的子串的哈希值为 \(h_r-h_{l-1}\times p^{r-l+1}\)，其中 \(p\) 的幂次可以预处理。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

typedef unsigned long long ull;

const int N = 1e5+10;
const int P = 13331;

int n, m;
char s[N];
ull h[N], p[N];

ull get_hash(int l, int r) {
    return (h[r] - h[l-1] * p[r-l+1]);
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0), cout.tie(0);
    
    cin >> n >> m >> s+1;
    h[0] = 0, p[0] = 1;
    for (int i = 1; i <= n; ++i) {
        h[i] = h[i-1] * P + (s[i] - 'A' + 1);
        p[i] = p[i-1] * P;
    }
    
    int l1, r1, l2, r2;
    while (m -- ) {
        cin >> l1 >> r1 >> l2 >> r2;
        ull h1 = get_hash(l1, r1), h2 = get_hash(l2, r2);
        if (h1 == h2) puts("Yes");
        else puts("No");
    }
    
    return 0;
}

标签：数据结构,idx,int,le,include,节点,op
From： https://www.cnblogs.com/Jasper08/p/16907618.html

2. 数据结构（I）

2. 数据结构（I）

2.1 链表

2.1.1 单链表

2.1.2 双链表

2.2 栈

2.2.1 模拟栈

2.2.2 单调栈

2.3 队列

2.3.1 模拟队列

2.3.2 单调队列

2.4 KMP 字符串算法

2.5 Trie 树

2.5.1 字典 Trie

2.5.2 01 Trie

2.6 并查集

2.7 堆

2.8 哈希表

2.8.1 普通哈希

2.8.2 字符串哈希

相关文章

赞助商

阅读排行