题目链接

A B C

A

这个套路已经出现了很多次了

就是两条线之间的网格图路径数，做法呢就是容斥

题意

求满足以下条件的 \(n\times m\) 的矩阵的个数对 \(10^9+7\) 取模

对于矩阵中的第 \(i\) 行第 \(j\) 列的元素 \(x_{i,j}\) 都有

• \(x_{i,j}< x_{i,j+1}\)
• \(x_{i,j}< x_{i-1,j+1}\)
• \(0\le x_{i,j} \le m\)

题解

首先注意到每一行都有 \(m\) 个数，是单增的，而且每个数 \(\in [0,m]\)

这说明每一行一定是从 \(0,\dots,m\) 删去一个数

我们记 \(a_i\) 表示每一行删去的数

现在我们考虑 \(x_{i,j}< x_{i-1,j+1}\) 这个条件

画几张图就可以看出， \(x_{i,j}< x_{i-1,j+1} \Leftrightarrow a_{i+1}\ge a_i-1\)

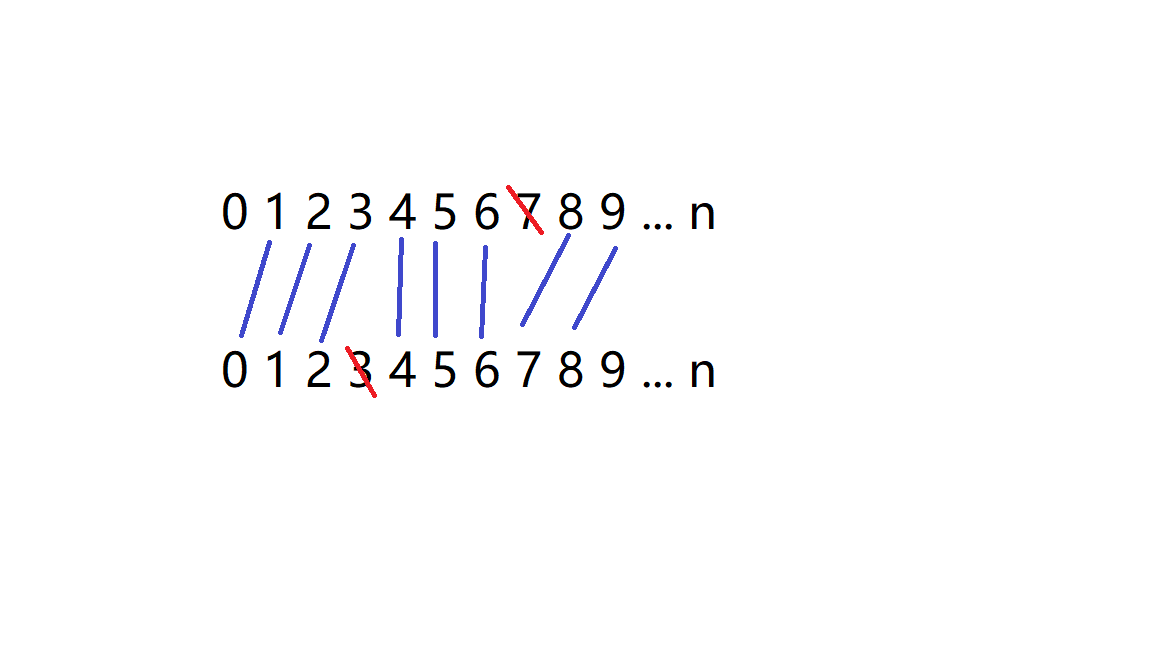
也就是说，原问题被转换成了这样子：

有一个长度为 \(n\) 的序列 \(\{a_i\}\) ，求满足 \(a_i\in [0,m]\) 且 \(a_{i+1}\ge a_i-1\) 的序列数

如果把题目改成 \(a_{i+1}\ge a_i\)，这个比较好做

这样一个 \(a_i\) 序列可以与一条从 \((1,0)\) 到 \((n+1,m)\) 的单调路径一一对应

（就直接让 \(a_i\) 取 \(1,\dots, n\) 处路径的最大值就好啦）

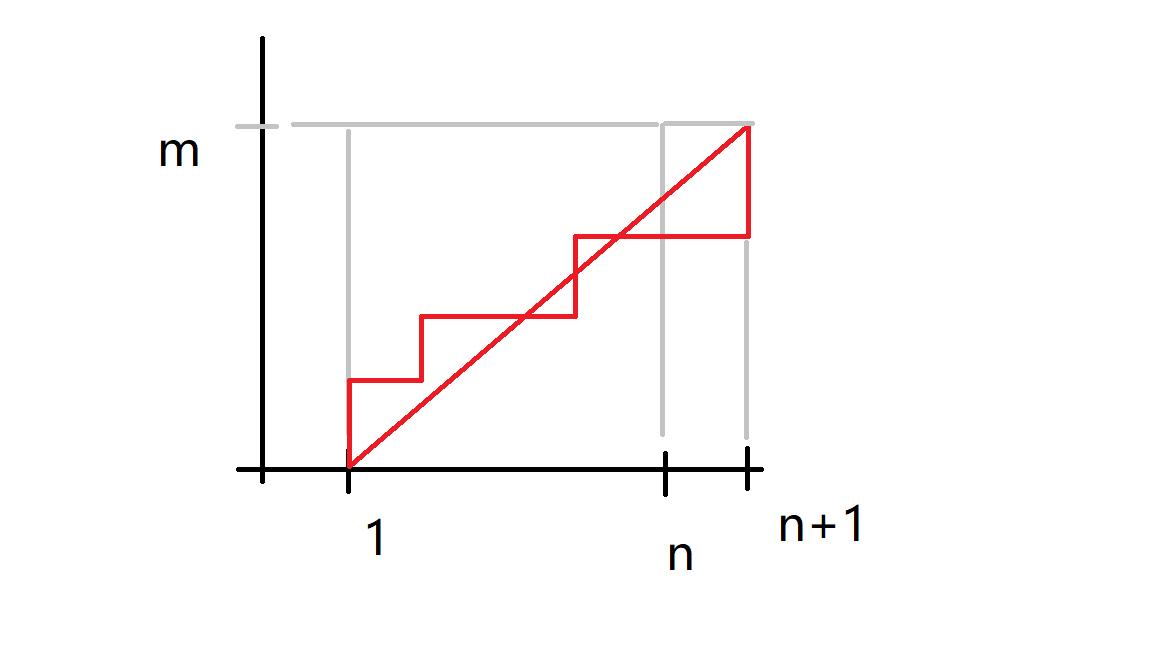
那么序列数就是 \(\displaystyle\binom{n+m}{m}\).

那我们来考虑原问题，原问题其实也可以转化为类似的问题

我们定义 \(b_i=a_i+i\) 这样是不是就是 \(b_{i+1}\ge {b_i}\)

但是这个时候， \(b_i \in [i,m+i]\)

也就是说，我们求的是 \((1,0)\) 到 \((n+1,n+m+1)\) 的路径数

而且路径不能越过 $y=x-1 $ 和 $ y=m$

转换到从原点开始，就是 $(0,0) \rightarrow (n,n+m+1) $ 的路径数

不能越过 \(y=x\) 和 \(y=m+1\)

然后呢，就是容斥，具体看这篇博客（！！还没补）

代码很好写

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 3e6+5, P = 1e9+7;
int n,m,fc[N],fci[N];
int ksm(int a, int b)
{
	int res=1;
	for(; b; b>>=1,a=(ll)a*a%P) if(b&1) res=(ll)a*res%P;
	return res;
}
int C(int x, int y)
{
	if(x<0 or y<0 or x<y) return 0;
	return (ll)fc[x]*fci[y]%P*fci[x-y]%P;
}
struct point { int x,y; }; //点
void refl(point &p, int b) { point q={p.y-b,p.x+b}; p=q; } //点沿着直线 y=x+b 反射

int main()
{
	fc[0]=1;
	for(int i=1; i<N; i++) fc[i]=(ll)fc[i-1]*i%P;
	fci[N-1]=ksm(fc[N-1],P-2);
	for(int i=N-1; i; i--) fci[i-1]=(ll)fci[i]*i%P;
	//for(int i=0; i<=10; i++) printf("%d %d\n",fc[i],fci[i]);
	scanf("%d%d",&n,&m);
	point p={n,n+m+1};
	ll res=C(p.x+p.y,p.x);
	point q=p;
	for(int i=-1; ; i=-i)
	{
		if(i<0) refl(q,-1); //y=x-1
		else refl(q,m+2); //y=m+2
		if(q.x<0 or q.y<0) break;
		res=(res+i*C(q.x+q.y,q.x)+P)%P; //容斥
	}
	q=p;
	for(int i=-1; ; i=-i)
	{
		if(i>0) refl(q,-1);
		else refl(q,m+2);
		if(q.x<0 or q.y<0) break;
		res=(res+i*C(q.x+q.y,q.x)+P)%P;
	}
	printf("%lld\n",res);
	return 0;
}

B

一道斯坦纳树的板子题

（为什么斯坦纳没有发起进攻，因为他去学信竞了\bushi）

斯坦纳树的学习笔记看这里（！！！还没补）