首页 > 其他分享 >PAM 学习笔记

PAM 学习笔记

时间：2022-11-16 07:11:15浏览次数：72  
标签：tot int pos len 学习 笔记 fail PAM 回文

\(PAM\)

回文树（也叫回文自动机），是一个可以存储一个串中所有回文子串的高效数据结构，回文树由转移边与 \(fail\) 指针构成，每个节点保存一个回文子串。转移边类似 \(trie\) 上的边， 但又并非代表在原节点代表的回文串后加一个字符，而是在其前后各加一个字符；\(fail\) 指针指向的是当前节点所代表的回文子串的最长回文后缀所在的节点。我们还需要维护每个节点的 \(len\)，同时根据需要还可以维护 \(cnt\) （当前节点所代表的回文子串的出现次数），\(trans\) 指针（指向小于等于当前节点所代表的回文串长度一半的最长回文后缀所在节点）。

回文树可以高效解决下列问题：

\(\bullet\; 1\) 求原串中本质不同的回文串个数

\(\bullet\; 2\) 求原串中本质不同的回文串出现次数

\(\bullet\; 3\) 最小回文划分

\(\bullet\; 4\) 原串中以 \(i\) 为结尾的最长回文子串

\(\bullet\; 5\) 一些有关回文串的 \(DP\) 问题

现在来讲一下回文树的具体实现

我们首先需要几样东西

\(trie[MAXN][26]\) 表示我们的转移边（当然你也可以用邻接表实现，邻接表的空间复杂度较低）。

\(fail[MAXN]\) 表示我们的 \(fail\) 指针。

\(len[MAXN]\) 表示我们当前节点所代表的回文子串的长度。

奇根，偶根。因为我们的回文串有偶回文串与奇回文串之分，我们就加入奇根，偶根两个虚根来方便我们操作。

其次我们采用增量法 （就是一个一个向自动机中增添字符）构建 \(PAM\) ，我们考虑如何将一个字符插入回文树。

我们发现我们插入时，其实是在回文树上找一个最长回文后缀，满足他之前一个字符与当前插入字符相同，我们设这个最长回文后缀所在的节点为 \(Fail\)，那么我们相当于是将 \(Fail\) 所代表的回文串的前后各加一个当前字符组成了新的一个回文串，如果我们没有出现过这个回文串，我们就新建一个节点 \(x\)，代表在 \(Fail\) 所代表的回文串前后新加一个当前字符所组成的回文串，而我们有转移边 \(trie[Fail][u]\)（\(u\) 为当前的字符，相当于这条边的边权为 \(u\)），所指向的节点即为我们当前新建的节点 \(x\)；那么我们 \(len_x=len_{Fail}+2\)，\(x\) 的 \(fail\) 指针通过接着向上找最长回文后缀满足他之前一个字符与当前插入字符的节点，这个节点即为 \(fail\) 指向的节点，具体实现如下：

int getfail(int x,int pos){
        while(pos-len[x]-1<0||s[pos-len[x]-1]!=s[pos])x=fail[x];
        return x;
    }
void insert(int pos){
    int u=s[pos]-'a';
    int Fail=getfail(pre,pos);
    if(!trie[Fail][u]){
        len[++tot]=len[Fail]+2;
        fail[tot]=trie[getfail(fail[Fail],pos)][u];
        trie[Fail][u]=tot;
    }
    pre=trie[Fail][u];
}

当然，我们需要注意边界条件，即为 \(fail_{even}=odd,len_{odd}=-1,tot=1\)，也就是说，我们偶根向上的 \(fail\) 指针为奇根（因为奇根不可能失配），奇根的长度初始化为 \(-1\)，方便以后的处理。

那么我们就建好了一个回文自动机，他的时间复杂度很优秀，为 \(O(|S|)\)，但空间复杂度很差，大约为 \(O(C|S|)\) （\(C\) 为字符集大小），所以在内存小的时候通常考虑使用邻接表存图。

关于一个字符串 \(aabaa\)，他的回文自动机建好大概是长这样，有边权的为转移边，无边权的为 \(fail\) 指针。

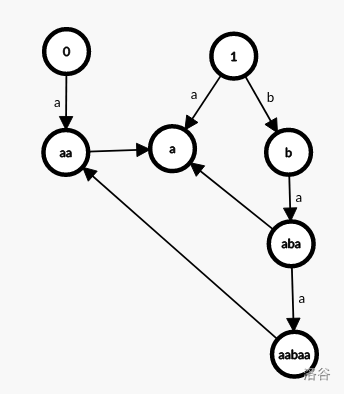
我们讲一下实际应用。

首先通过回文自动机，我们可以找到一个字符串中所有的本质不同的回文子串，回文自动机保存的其实就是一个字符串所有的本质不同的回文子串。

其次，我们可以通过回文自动机方便的求出每一个回文子串的出现次数，和 \(AC\) 自动机不一样的是，\(AC\) 自动机的构建没有用到增量法，\(fail\) 指针无序，所以他的统计是需要通过拓扑实现的。而回文自动机先天要求 \(fail\) 有序，即由编号大的节点指向编号小的节点，那么我们就可以通过 \(for\) 循环方便快捷的求出每一个回文子串出现的次数。

for(int i=tot;i>=2;i--){
    cnt[fail[i]]+=cnt[i];
}

通常我们还需要找到一个 \(trans\) 指针，指向长度小于等于当前节点所代表的字符串的最长回文后缀的节点，我们下面会讲几道例题来学习一下。

\(NO.1\)

\(【模板】回文自动机（PAM）\)

这是道模板题，我们可以发现因为我们是用增量法构建回文树的，那么就支持动态求解。考虑对于以一个点结尾的回文串个数，其实就是他在 \(fail\) 树上跳的次数，那么他的个数就是其 \(fail\) 指针所指向节点的答案加 \(1\)。

\(code\)

#include<bits/stdc++.h>
using namespace std;
const int N=5e5+10;
int ans=0;
char s[N];
struct PAM{
    int trie[N][26],fail[N],res[N],pre,tot,len[N];
    inline void init(){fail[0]=1,len[1]=-1,tot=1;}
    int getfail(int x,int pos){
        while(pos-len[x]-1<0||s[pos-len[x]-1]!=s[pos])x=fail[x];
        return x;
    }
    inline void insert(int u,int pos){
        int Fail=getfail(pre,pos);
        if(!trie[Fail][u]){
            len[++tot]=len[Fail]+2;
            fail[tot]=trie[getfail(fail[Fail],pos)][u];
            res[tot]=res[fail[tot]]+1;
            trie[Fail][u]=tot;
        }
        pre=trie[Fail][u];
        ans=res[pre];
        printf("%d ",ans);
    }
}A;
int main(){
    scanf("%s",s+1);
    int len=strlen(s+1);
    A.init();
    for(int i=1;i<=len;i++){
        int t=(s[i]-97+ans)%26;
        s[i]=t+97;
        A.insert(t,i);
    }
    return 0;
}

\(NO.2\)

\(回文串\)

这题显然比板子还板子，我们发现我们需要统计的就是我们上文提到的 \(cnt\) 数组与 \(len\) 数组的乘积最大，那么我们可以通过回文自动机快速求解。

\(code\)

#include<bits/stdc++.h>
using namespace std;
const int N=3e5+10;
long long ans=0;
struct PAM{
    int trie[N][26],cnt[N],fail[N],len[N],tot,pre,n;
    char s[N];
    void init(){
        fail[0]=1,len[1]=-1,tot=1;
        scanf("%s",s+1);
        n=strlen(s+1);
    }
    int getfail(int x,int pos){
        while(pos-len[x]-1<0||s[pos-len[x]-1]!=s[pos])x=fail[x];
        return x;
    }
    void insert(int pos){
        int u=s[pos]-'a';
        int Fail=getfail(pre,pos);
        if(!trie[Fail][u]){
            len[++tot]=len[Fail]+2;
            fail[tot]=trie[getfail(fail[Fail],pos)][u];
            trie[Fail][u]=tot;
        }
        pre=trie[Fail][u];
        cnt[pre]++;
    }
    void Insert(){
        for(int i=1;i<=n;i++)insert(i);
    }
    void print(){
        for(int i=tot;i>=2;i--){
            cnt[fail[i]]+=cnt[i];
            ans=max(ans,1ll*len[i]*cnt[i]);
        }
        printf("%lld\n",ans);
    }
}A;
int main(){A.init(),A.Insert(),A.print();return 0;}

\(NO.3\)

\(秩序魔咒\)

这道题让我们求出两个字符串的最长公共回文串的长度及个数，我们可以关于每个字符串建一个回文自动机，然后同时在两个回文自动机上 \(DFS\)，找出公共的最长的字符串个数及长度即可。

注意回文自动机有两个根，一个奇根，一个偶根，注意两个根都得遍历。

\(code\)

#include<bits/stdc++.h>
using namespace std;
const int N=3e5+10;
int tong[N];
inline int read(){int x=0,f=0;char ch;while(!isdigit(ch=getchar()))if(ch=='-')f=1;do{x=(x<<1)+(x<<3)+(ch^48);}while(isdigit(ch=getchar()));return f?-x:x;}
struct PAM{
    int trie[N][26],fail[N],len[N],pre,tot,n;
    char s[N];
    void init(){
        fail[0]=1,len[1]=-1,tot=1;
        scanf("%s",s+1);
        n=strlen(s+1);
    }
    int getfail(int x,int pos){
        while(pos-len[x]-1<0||s[pos-len[x]-1]!=s[pos])x=fail[x];
        return x;
    }
    void insert(int pos){
        int u=s[pos]-'a';
        int Fail=getfail(pre,pos);
        if(!trie[Fail][u]){
            len[++tot]=len[Fail]+2;
            fail[tot]=trie[getfail(fail[Fail],pos)][u];
            trie[Fail][u]=tot;
        }
        pre=trie[Fail][u];
    }
    void Insert(){
        for(int i=1;i<=n;i++)insert(i);
    }
}A,B;
void dfs(int x,int y){
    if(x+y>2)tong[A.len[x]]++;
    for(int i=0;i<26;i++){
        if(A.trie[x][i]&&B.trie[y][i]){
            dfs(A.trie[x][i],B.trie[y][i]);
        }
    }
}
int main(){
    int lim=(read(),read());
    A.init(),A.Insert();
    B.init(),B.Insert();
    dfs(0,0),dfs(1,1);
    for(int i=lim;i>=1;i--){
        if(tong[i]){
            printf("%d %d\n",i,tong[i]);
            return 0;
        }
    }
    return 0;
}

\(NO.4\)

\([JSOI2013]快乐的 JYY\)

这个题与上面两道很相似，做法就是同时在两个回文自动机上 \(DFS\)，并统计答案即可。

\(code\)

#include<bits/stdc++.h>
using namespace std;
const int N=5e4+10;
long long ans=0;
struct PAM{
    int trie[N][26],fail[N],tot,pre,n,cnt[N],len[N];
    char s[N];
    void init(){
        fail[0]=1,len[0]=0,len[1]=-1,tot=1;
        scanf("%s",s+1);
        n=strlen(s+1);
    }
    int getfail(int x,int pos){
        while(pos-len[x]-1<0||s[pos-len[x]-1]!=s[pos])x=fail[x];
        return x;
    }
    void insert(int pos){
        int u=s[pos]-'A';
        int Fail=getfail(pre,pos);
        if(!trie[Fail][u]){
            len[++tot]=len[Fail]+2;
            fail[tot]=trie[getfail(fail[Fail],pos)][u];
            trie[Fail][u]=tot;
        }
        pre=trie[Fail][u];
        cnt[pre]++;
    }
    void Insert(){for(int i=1;i<=n;i++)insert(i);}
    void get(){for(int i=tot;i;i--)cnt[fail[i]]+=cnt[i];}
}A,B;
void dfs(int x,int y){
    if(x+y>2)ans+=1ll*A.cnt[x]*B.cnt[y];
    for(int i=0;i<26;i++){
        if(A.trie[x][i]&&B.trie[y][i]){
            dfs(A.trie[x][i],B.trie[y][i]);
        }
    }
}
int main(){
    A.init(),A.Insert(),A.get();
    B.init(),B.Insert(),B.get();
    dfs(1,1);dfs(0,0);
    printf("%lld\n",ans);
    return 0;
}

\(No.5\)

\([SHOI2011]双倍回文\)

这个题很好地运用了 \(trans\) 指针，我们对于一个字符串，他的 \(trans\) 指向的节点所对应的字符串的长度为他的一半，且 \(trans\) 指针所对应的字符串是一个偶回文串时，这个回文串就是一个双倍回文，求解 \(trans\) 指针后判断即可。

\(code\)

#include<bits/stdc++.h>
using namespace std;
const int N=5e5+10;
struct PAM{
    int trie[N][26],fail[N],trans[N],tot,pre,n,len[N];
    char s[N];
    void init(){
        fail[0]=1,len[1]=-1,tot=1;
        scanf("%d%s",&n,s+1);
    }
    int getfail(int x,int pos){
        while(pos-len[x]-1<0||s[pos-len[x]-1]!=s[pos])x=fail[x];
        return x;
    }
    int gettrans(int x,int pos){
        while(((len[x]+2)<<1)>len[tot]||s[pos-len[x]-1]!=s[pos])x=fail[x];
        return x;
    }
    void insert(int pos){
        int u=s[pos]-'a';
        int Fail=getfail(pre,pos);
        if(!trie[Fail][u]){
            len[++tot]=len[Fail]+2;
            fail[tot]=trie[getfail(fail[Fail],pos)][u];
            trie[Fail][u]=tot;
            if(len[tot]<=2)trans[tot]=fail[tot];
            else{
                int Trans=gettrans(trans[Fail],pos);
                trans[tot]=trie[Trans][u];
            }
        }
        pre=trie[Fail][u];
    }
    void Insert(){for(int i=1;i<=n;i++)insert(i);}
    void print(){
        long long ans=0;
        for(int i=1;i<=tot;i++){
            if(len[trans[i]]%2==0&&len[trans[i]]*2==len[i])ans=max(ans,1ll*len[i]);
        }
        printf("%lld\n",ans);
    }
}A;
int main(){A.init(),A.Insert(),A.print();return 0;}

\(No.6\)

\(Virus synthesis\)

一道 \(DP\)，我们可以发现最后的串一定是由一个偶回文串加上若干零散字符构成的（因为这样用到了 \(2\) 操作，而用 \(2\) 操作一定比用若干个 \(1\) 操作更优），那么我们考虑对整个串建出回文自动机，那么我们设 \(dp_i\) 为拼出 \(i\) 这个回文串需要的最少步数，那么我们考虑转移。

首先，我们设 \(i\) 为 \(j\) 在回文树上的儿子，那么我们有转移

\[dp_i=min(dp_j+1) \]

因为我们可以通过先拼出 \(j\) 的一半，再加一个新的字符，构成 \(i\) 的一半，再用 \(2\) 操作拼出 \(i\)，即为 \(dp_i=(dp_j-1)+1+1\)

其次，我们设 \(p\) 为 \(i\) 的 \(trans\) 指针，那么我们有转移

\[dp_i=min(dp_p+len_i/2-len_p+1) \]

意味我们可以通过他的 \(trans\) 指针所指向的回文串，再在上面加上 \(len_i/2-len_p\) 个字符，再用一次 \(2\) 操作拼出 \(i\)。

\(code\)

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10;
struct PAM{
    int fail[N],trie[N][4],trans[N],len[N],dp[N],q[N],l,r,tot,pre,n,ans;
    char s[N];
    int change(char c){
        if(c=='A')return 0;
        else if(c=='T')return 1;
        else if(c=='C')return 2;
        return 3;
    }
    void init(){
        fail[0]=1,len[1]=-1,tot=1,pre=0,l=1,r=0;
        scanf("%s",s+1);
        n=strlen(s+1);
        ans=n;
    }
    int getfail(int x,int pos){
        while(pos-len[x]-1<0||s[pos-len[x]-1]!=s[pos])x=fail[x];
        return x;
    }
    int gettrans(int x,int pos){
        while(((len[x]+2)<<1)>len[tot]||s[pos-len[x]-1]!=s[pos])x=fail[x];
        return x;
    }
    void insert(int pos){
        int u=change(s[pos]);
        int Fail=getfail(pre,pos);
        if(!trie[Fail][u]){
            len[++tot]=len[Fail]+2;
            fail[tot]=trie[getfail(fail[Fail],pos)][u];
            trie[Fail][u]=tot;
            if(len[tot]<=2)trans[tot]=fail[tot];
            else{
                int Trans=gettrans(trans[Fail],pos);
                trans[tot]=trie[Trans][u];
            }
        }
        pre=trie[Fail][u];
    }
    void Insert(){for(int i=1;i<=n;i++)insert(i);}
    void getans(){
        for(int i=2;i<=tot;i++)dp[i]=len[i];
        l=1,r=0;
        q[++r]=0,dp[0]=1;
        while(l<=r){
            int cc=q[l++];
            dp[cc]=min(dp[cc],dp[trans[cc]]+len[cc]/2-len[trans[cc]]+1);
            ans=min(ans,dp[cc]+n-len[cc]);
            for(int i=0;i<4;i++){
                int v=trie[cc][i];
                if(!v)continue;
                dp[v]=min(dp[v],dp[cc]+1);
                q[++r]=v;
            }
        }
        printf("%d\n",ans);
        for(int i=0;i<=tot;i++)for(int j=0;j<4;j++)trie[i][j]=0;
    }
}A;
int main(){
    int T=0;
    scanf("%d",&T);
    while(T--)A.init(),A.Insert(),A.getans();
    return 0;
}

标签：tot,int,pos,len,学习,笔记,fail,PAM,回文
From： https://www.cnblogs.com/hxqasd/p/16894663.html

相关文章

  • 第二章读书笔记
    03运行超市抹零结账行为money_all=56.75+72.91+88.50+26.37+68.51money_all_str=str(money_all)print("商品总金额为："+money_all_str)money_real=int(money_all)money_rea......
  • 机器学习分析步骤
    1.提出问题2.理解数据 2.1数据清洗 2.2导入数据 2.3查看数据集信息   2.3.1Describe()描述统计信息   2.3.2info()发现缺失数据3.数据清洗 3.......
  • Python 文本文件拖上转自适应图片 - 学习笔记（2022.11.16）
    Python文本文件拖上转自适应图片功能：1、支持拖拽执行2、文本文件转为自适应尺寸图片1importre2importos3importsys4importtime5fromPI......
  • Win10 笔记本禁用/启用自带键盘
    文章来源：华硕笔记本怎么禁用自带键盘_虽千万里，吾往矣！的博客-CSDN博客_华硕笔记本怎么禁用自带键盘在小娜搜索栏中输入cmd，找到命令提示符（cmd），并且右键以管理员身份运行。......
  • 强化学习代码实战-07 Actor-Critic 算法
    Actor（策略网络）和Critic（价值网络）Actor要做的是与环境交互，并在Critic价值函数的指导下用策略梯度学习一个更好的策略。Critic要做的是通过Actor与环境交互收集的数......
  • 哈希算法学习笔记 I：XOR hashing
    咕咕中，两天后填坑。CF1175F.TheNumberofSubpermutations求一个序列中是排列的子串数量。CF1746F.Kazaee多组询问，求一个序列的\([l,r]\)段是否为排列。......
  • 【论文笔记】CBIR的最近发展 - Recent developments of content-based image retrieva
    原文地址Abstract随着互联网技术的发展和数字设备的普及，基于内容的图像检索(Content-BasedImageRetrieval,CBIR)迅速的发展、应用，涉及计算机视觉和人工智能的各个......
  • Mysql操作学习总结
    Cmd控制台mysql-uroot-p--连接数据库flushprivileges;--刷新权限showdatabates;--查看所有的数据库use数据库名;--切换数据库showtables;--查看数据......
  • vue学习面试题整理（day01）
    一、Vue的最大优势是什么？  简单易学，轻量级整个源码js文件不大，双向数据绑定，数据驱动视图，组件化，数据和视图分离，vue负责关联视图和数据，作者是中国人（尤雨溪），文档都是中文的，......
  • go语言学习
    安装、配置以及测试：https://cloud.tencent.com/developer/article/1623121go的两种运行方式：gorunhello.go#直接运行go程序gobuildhello.go#编译得到二进制文......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99