标签：温变 热应力 材料 SOL TREF 参数 计算 Nastran 温度

Nastran中温变材料设置

在Patran中若需要设置材料参数随温度变化，需要先设置material field，选择关于温度变化，从而能够定义温度-材料参数曲线，进而在材料参数设置中选择对应场即能附上。以各向同性MAT1为例，对应在bdf卡片中，温变材料以MATT1卡片体现，温度-材料参数数据则体现在TABLEM1卡片中。

TABLEM1的格式与数据要求与其他各类table类似，如其线性插值等特性，相关要求在官方手册quick reference guide.pdf中有详细介绍，这儿就放一张我认为最重要的图。

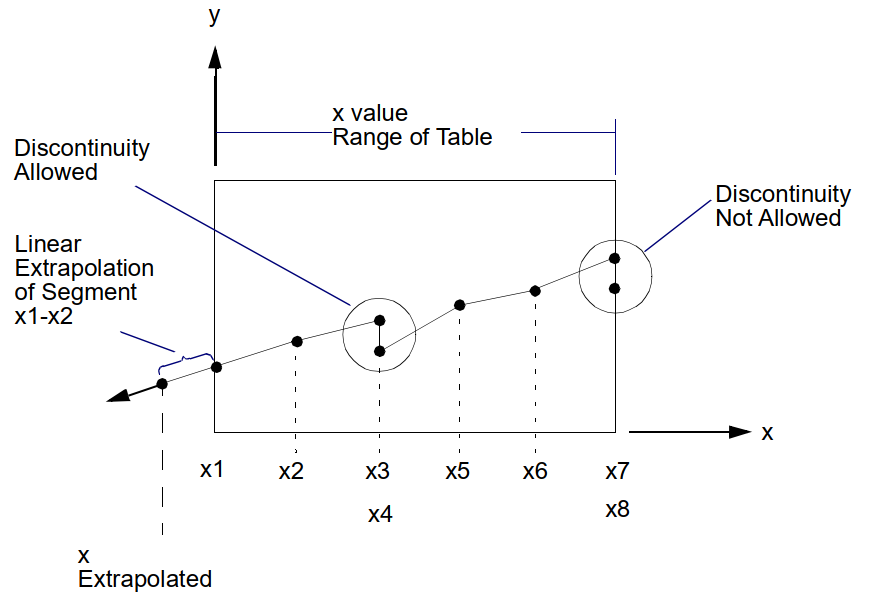
MATT1卡片需要与对应材料MAT1的卡片同编号。值得注意的是，根据手册要求，在弹性模量、剪切模量、泊松比三者中任一参数是温变时，三者的温度-参数数据都应给出。

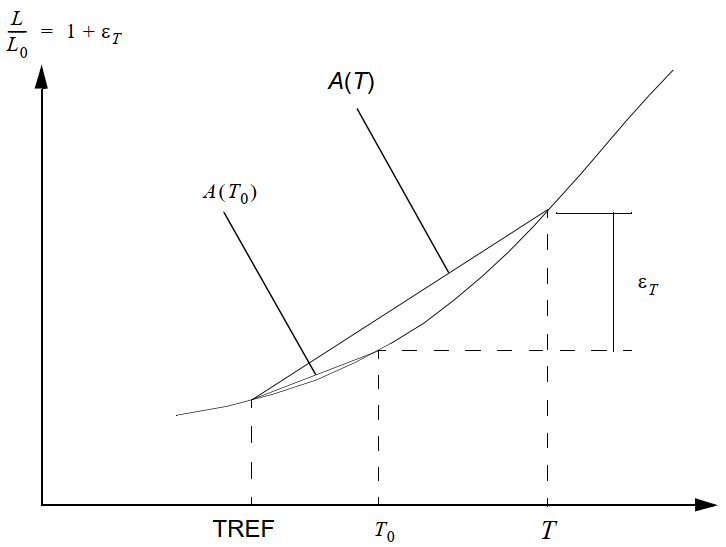
在MAT1卡片中有一个与温度相关的参数TREF，在除了SOL 106外的求解中，起到了和TEMPERATURE(INITIAL)相同的作用。然而在SOL 106中，TREF的设置却关系到热膨胀系数的使用。笔者认为手册中相关描述比较拗口，但手册中的示意图与公式却时很明白的。热应变的计算需要同时考虑TREF和TEMPERATURE(INITIAL)的温度，即手册中所用公式：

\[\varepsilon_T = A\left(T\right)\cdot\left(T-TREF\right) - A\left(T_0\right)\cdot\left(T-TREF\right) \]

因此设置正确的TREF是十分重要的，否则字段为空时将采用默认值0，可能会带来计算错误。下文也会有个简单的例子。

应当采用非线性静力学计算热应力

以一块 \(800mm\times300mm\times5mm\) 的矩形板为例，材料参数如下表，看看相关参数设置以及求解器的计算结果。

Temperature/℃	Young's modulus/GPa	Poisson's ratio/GPa	Shear modulus	Thermal expansion coefficient/\(\times10^{-6}\)
0	220	88.7	0.24	0
20	200	80.6	0.24	2
100	120	48.4	0.24	10

分析屈曲临界温度，约80℃，设TREF与初始温度为20℃，载荷温度为60℃。首先可以通过设置悬臂边界（注意要释放边界节点Y方向约束以防边界应力干扰），根据热膨胀后位移来判断计算结果。此时结果正确，若未设TREF，则TREF取默认值0，计算所得梁端位移为\(2.56\times10^{-4}mm\)。

然而若选用SOL 101计算该算例，梁端位移为\(6.4\times10^{-5}mm\)，简单计算可知这个值是在20℃下的参数所得的。进一步对比在两边固支（同样释放边界Y方向约束）下的X方向应力结果，SOL 106所得\(\sigma_x=-3.84\times10^7Pa\)，而SOL 101所得\(\sigma_x=-1.6\times10^7Pa\)。因此在温变材料的参数取值上，应当基于SOL 106非线性静力学进行热应力的计算。

问题讨论

值得注意的是，务必要确保屈曲温度的正确计算。在笔者进行算例计算时，由于为了突出效果，将弹性模量等参数随温度的变化设置很明显，因此温度越高模量越低所能承载面内载荷越小。若此时温度载荷不小心稍微超过了临界温度从而使结构实际到达屈曲后，非线性的计算需要注意参数设置：在载荷步取默认10步时，计算结果还体现为线性结果未有面外位移，但增大载荷步后即有屈曲的体现了。但是笔者不知为何，在SOL 106下勾选屈曲选项后报错。因此仅能基于SOL 105计算。屈曲是个神奇的问题，非线性这块笔者也接触很少，有待进一步学习。

*** USER INFORMATION MESSAGE 6186 (NCONVG)
*** SOLUTION HAS CONVERGED ***
SUBID 1 LOOPID 10 LOAD STEP 1.000 LOAD FACTOR 1.00000000

*** USER INFORMATION MESSAGE 9005 (SUBDMAP NLSTATIC)
THE SOLUTION FOR LOOPID= 10 IS SAVED FOR RESTART
^^^
*** USER INFORMATION MESSAGE 22713 (SUBDMAP SEKDR)
PARAMETER EXCLUDE IS NOT DEFINED DIFFERENTIAL STIFFNESS IS COMPUTED FOR ALL ELEMENTS.
^^^
^^^
*** USER INFORMATION MESSAGE 9051 (SUBDMAP NLSTATIC)
BUCKLING ANALYSIS INITIATED FOR LOOP ID=BUCKLING
^^^
*** SYSTEM FATAL MESSAGE 6704 (DFMFRS)
LOGIC ERROR 2 IN NUMERIC PHASE OF SPARSE DECOMPOSITION.
USER ACTION: INCREASE MEMORY BY 33670451 WORDS.

另一方面，以上算例的边界还是释放了Y方向约束的，若在边界节点上全约束，线性和非线性静力学计算的位移结果略有不同，从而导致应变以及应力也都有区别，这也是计算过程中需要注意的问题。笔者认为这可能和非线性迭代过程产生的误差有关，因此笔者目前认为如果需要更精确的结果，是否可以通过给各个单元根据单元温度单独幅材料属性可以解决？虽然这种方法可能需要编程实现且工作量不小。

SOL 101计算的\(\sigma_x\)	SOL 106计算的\(\sigma_x\)

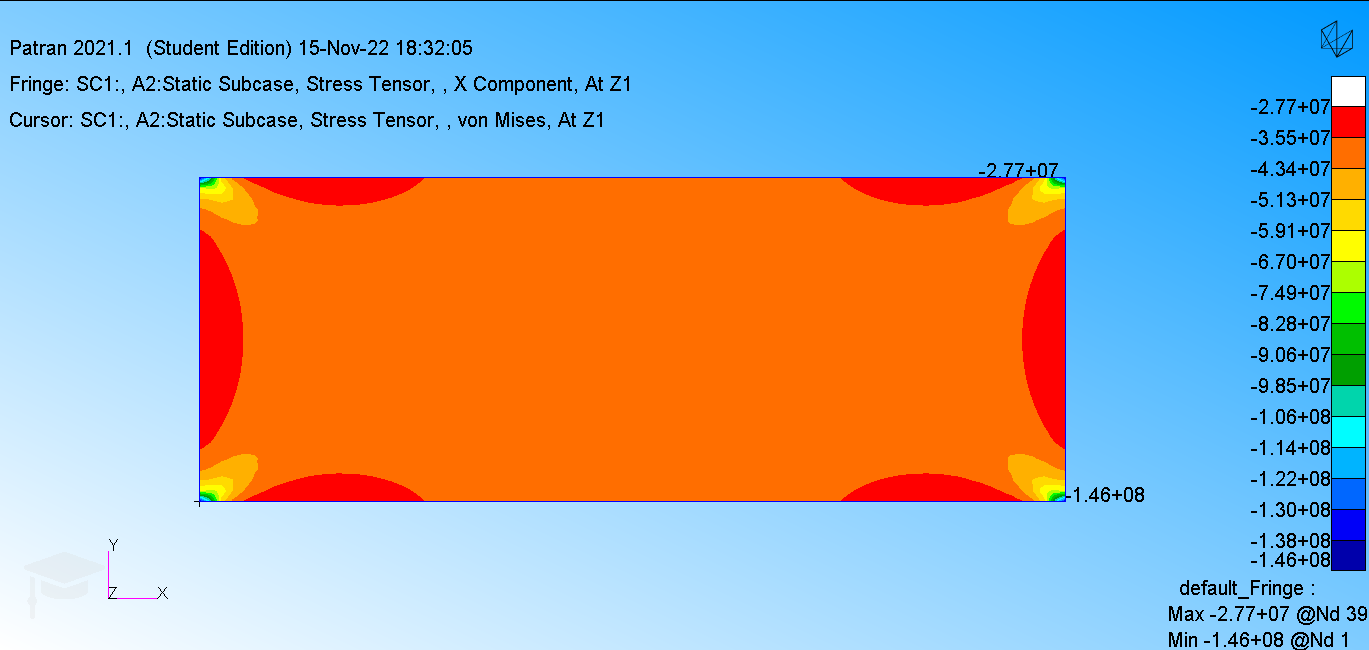其实这是个很简单的问题，然而就我这次的经历来看，一来是因为参考资料较少，二来是因为自己一开始的调试不得当，导致在其上花费了许多时间，希望能够帮助到刷到这篇博客的有缘人。不过有意思的是，TREF的问题在手册中明确提到了，但为何必须使用线性求解下材料参数不是根据目标载荷温度而定还没找到明确说明，权当一个自己试出来的经验吧。更进一步地， 热环境下动响应的计算需要基于非线性结果开展，此时无法直接像SOL 101一样直接用preload，而需要进行重启动设置，当然使用SOL 400可能也是一种方法，但关于瞬态响应一直未能成功提交计算。这块内容笔者算是也挖了一个坑等待后边有空来填哈哈。也欢迎各位同学老师讨论指教。

标签：温变,热应力,材料,SOL,TREF,参数,计算,Nastran,温度
From： https://www.cnblogs.com/bfrf/p/16893507.html