zzszoi 20221112 记录
作者 zzafanti(FreshOrange) 请勿转载
前言
这次出题相对前三次模拟赛来说难度有所加大,也只有三道题。
第一道是基础的数学题,有思维含量。
第二道是比较好想的计数题,暴力也很好打,数据范围不是非常大(我觉得\(O(n^2)\)暴力应该卡的过去)
第三道是个我觉得不太好想的dp题,冲着五十分我打了个状压,实测50分极限数据5.0s内跑的出来,但是看到256MB的空间限制,毫无疑问照我的样子开数组要mle(ccf系列赛空间计算的是开了多少而不是用了多少),考虑空间优化,把几个数组滚了一滚,我size了一下c.exe,然后发现大于256MB......没办法,只能把数组开小,差不多卡到230MB,恐怕只有\(a_i\leq 2000\)的时候不RE了,事实证明……50%的点\(\exists a_i > 2000\),于是喜提暴力分&_&。(后来发现好像开\(unsigned ~int\)而不是占\(8byte\)的\(long long\)似乎就行了,但是当时测的时候\(p=1e9\)的情况下一直爆\(unsigned ~int\),可惜强制类型转化写的不好啊……而且有一个数组其实还可以滚掉一维……但是没调出来比赛就结束了……QAQ)
%%%%%% aker \(wangaofei\)
我的代码下载地址
题解
T1 游戏
题目描述
飞飞和壮壮在玩游戏,刚开始,飞飞手里有 \(N\) 块糖果,壮壮手里有 \(M\) 块糖果。游戏规则是这样的:每轮游戏中,他们会比较手中的糖果数量,如果他俩手里的糖果数量不相等,则拥有较少糖果数量的人会从对方手里拿走和他手里糖果相等的数量,这样的话,原先拥有较少糖果数量的人的糖果数量就翻倍了;如果两者的糖果数量相等,那么飞飞会拿走壮壮的糖果。
经过 \(K\) 轮以后,他俩都玩累了,准备享用糖果了。他俩想知道\(K\)轮以后,拥有较少糖果的人的糖果数量是多少呢?
输入格式
只有一行含三个正整数 \(N,M,K\)。
输出格式
输出俩人中较少的糖果数量。
输入样例
5 5 3
输出样例
0
样例解释
第 1 轮:飞飞拿走壮壮的 5 块糖果,此时飞飞有 10 块糖果,壮壮有 0 块糖果。
第 2 和第 3 轮中,都是壮壮拿走飞飞的 0 块糖果。
最终飞飞有 10 块糖果,壮壮有 0 块糖果。
数据范围
30%的数据,\(0\leq N,M,K\leq 10^5\),\(0<=N,M,K<=10^5\)
60%的数据,\(0\leq N,M\leq 10^5,0\leq K\leq 10^9,0\leq N , M \leq 10^5 ,0 \leq K\leq 10^9\)
100%的数据,\(0\leq N,M,K\leq 10^9\)
思路
首先,暴力很好打,如下
#include<bits/stdc++.h>
using namespace std;
const int N=1e9+10;
int main(){
long long n,m,k;
cin>>n>>m>>k;
while(k--){
if(n<=m){
m-=n;
n*=2;
}
else{
n-=m;
m*=2;
}
if(!(n&&m)){ //显然n,m其中一个为0后,下一轮游戏并不会造成两人糖果数量变化
cout<<min(n,m)<<'\n';
return 0;
}
}
cout<<min(n,m)<<'\n';
return 0;
} //同样,放进博客为了美观压了行qwq
这就有\(40pts\)了。呃,交代码前记得检查,把调试输出删去,并且在一些比赛中记得加文件读写哈!不要像这次\(sunchenxu\)一样……QAQ
考虑到\(k\leq 1e9\),
这种做法显然会超时很多点,
于是我们可以推一推性质,
不难发现,
当\(n<m\)时,
我们要\(m-n\),\(n\times 2\),
对于\(n\times 2\),很容易实现,
对于\(m-n\),可以发现
\(2m \equiv m-n \pmod{n+m}\)
于是我们可以直接将\(m\)乘2后模\(n+m\)。
可以发现,两个操作实际上都是乘2模(n+m),
于是可以得出,
记 \(t=n\times 2^k \bmod (n+m)\),
则答案为\(min\{t,m+n-t\}\) 。
上面的推导可以像这样直观理解:
将数轴负半轴割掉,非负半轴从原点开始依次划分若干个长度为\(k=m+n\)的区间,即\([0,k-1],[k,2k-1],[2k,3k-1].......\),
如图

那么我们选一个整点\(p \in [0,k-1]\),我们规定使得\([0,p]\)的糖果是飞飞的,\((p,k-1]\)的糖果的壮壮的,那么\(p\)就是他们的分界点。
*
假设此时\(p\)已经超过该区间的中点,我们依然让飞飞的糖果数量乘二。这时,\(p\)的位置向右移动了\(|p|\),如图,

观察一下,这时候对\(p\)模\((n+m)\),剩下的绿色部分不就是\(m-n\)吗,又由于\(m+n\)恒定不变,所以此时\(p\)依然是两人糖果的分界点。如图,
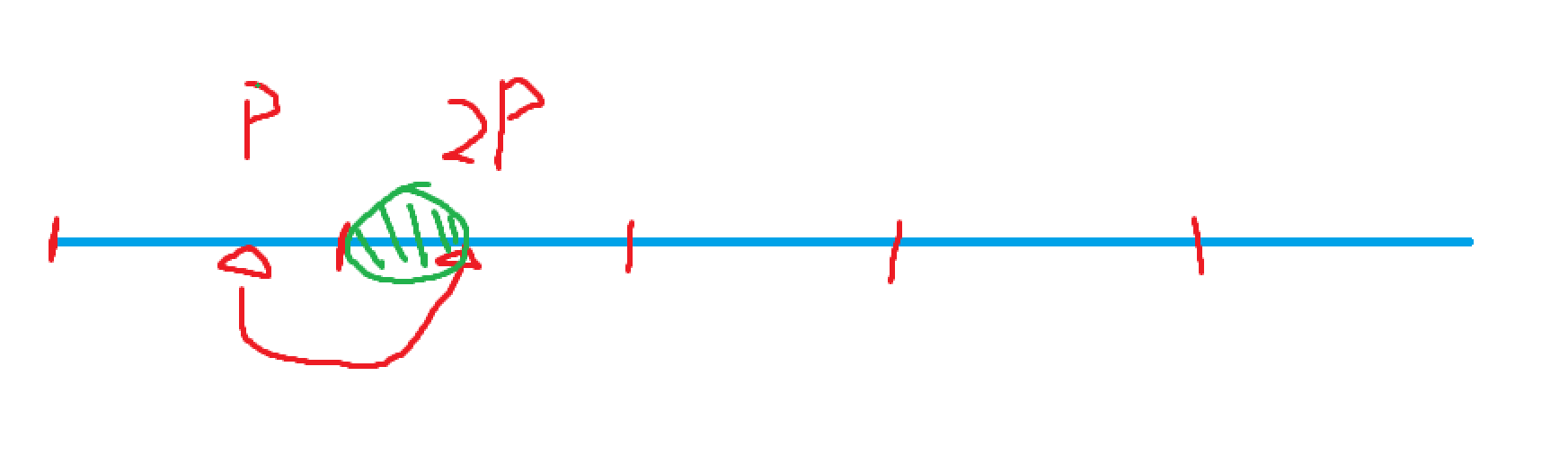
进而,我们可以得出与模意义下相同的结论。
好了好了
思路说完了,
如何求答案呢。
重点在于求\(2^k \bmod (n+m)\),
可以考虑使用快速幂,它在\(O(logb)\)的复杂度下可以算出\(a^b \bmod p\),原理是二进制拆分。\(O(logk)\)完全可以满足这道题。
具体如何实现快速幂可以参考蓝书第一章的位运算部分或者这个
参考代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n,m,k;
ll qpow(ll a,ll b){
ll p=2,ret=1;
for(; b; b>>=1){
if(b&1) ret=ret*p%m;
p=p*p%m;
}
return ret*a%m;
}
int main(){
cin>>n>>m>>k;
if(m==0||n==0){
puts("0");
return 0;
}
m+=n;
n=qpow(n,k);
cout<<min(n,m-n);
return 0;
}
T2 好的子数组
题目描述
一个数组 \(a\) 长度为 \(n\)。我们定义一个概念“坏对”:对于\((ax, ay)\),如果满足 \(x < y\),且 \(ax \bmod ay = k\),则\((ax, ay)\)是一个坏对。
那么有多少个连续子数组是好的呢,即不包含坏对?
输入格式
第一行输入两个正数 \(n\) 和 \(k\)。
第二行输入 \(n\) 个整数,表述数组 \(a\)。
输出格式
输出一行表示答案。
输入样例
3 2
5 3 1
输出样例
4
样例解释
只有一个坏对\((5, 3)\)。
数据范围
20%的数据,\(1\leq n\leq 100\)。
另外30%的数据,\(k=0\)。
100%的数据,\(1\leq n,k,a_i\leq 10^5\)。
思路
计数,显然,一个长度为\(n\)的数组的连续子数组个数有\(\frac{n\times (n+1)}{2} = O(n^2)\)个,所以这题不用取模,开\(long~long\)即可。
可以考虑枚举每个子数组左右端点,然后check一下这个子数组是否满足不含坏对的要求,略加优化即可,时间复杂度\(O(n^3)\)。可以得部分分。代码如下。
#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
const int N=100010;
int main(){
ull ans=0;
ull n,K,a[N];
cin>>n>>K;
for(int i=1; i<=n; i++){
scanf("%llu",&a[i]);
}
for(int i=1; i<=n; i++){
for(int j=i; j<=n; j++){
bool fg=0;
for(int k=j; k>i; k--){
if(a[i]%a[k]==K){
fg=1;
break;
}
}
if(!fg) ans++;
else break; //已经包含至少一组坏对,所以再向后移动j显然不能符合要求
}
}
cout<<ans<<endl;
return 0;
}
考虑换个想法或者优化。
我在一个月前做过一道类似的计数问题,正解双指针实现,很有趣。但是比这个题稍麻烦。
受那道题思路的影响,我想到了这道题的一个做法。
可以从前向后遍历数组,枚举子数组的右端点,设当前下标为\(i\),以\(i\)为右端点的合法子数组的个数有多少呢?可以这么考虑:
用\(lst[p]\)表示\(p\)在\([1,i-1]\)中出现的最靠右的位置。
我们可以发现,\(a[x]\bmod a[y] == k\)当且仅当\(a[y] \mid a[x]-k\),
于是我们对于\(a[i]\),可以枚举\(a[i]\)的所有倍数,然后查询他们的\(lst\),找到值最大的记作\(t\),特别地,若\(a_i \leq k\),取\(t=0\)
也就是说,\(\forall j(t<j\leq i)\),\(a[j] \bmod a[i] \ne k\),
但是\([j,i]\)就一定合法吗?
不一定
如果\(\exists j,l(t<j,l <i)\),使得\(a[j] \bmod a[l]=k\),那么这个数组依然不合法。
这时候,我们可以用\(f[i]\)来表示以\(i\)为右端点的合法子数组的最左端点的左一个下标。
特别的,\(f[0]=0\),
那么对于\(i\ne 0\),\(f[i]=max\{f[i-1],t\}\) (很明显数组\(f\)有单调性)
那么\(\forall j(f[i]<j\leq i),a[j]\bmod a[i]\ne k,\) 所以我们就得出了以\(i\)为右端点的合法子数组个数\(i-f[i]\)。答案即为\(\sum^n_{i=1} (i-f[i])\)。
考虑一下时间复杂度,
记\(s=max\{a_i\},1\leq i \leq n\),
那么因为要算每个数的倍数,所以每次枚举右端点要计算\(O(\frac{s}{a_i})\)次,总共就是\(O(\sum^n_{i=1} \frac{s}{a_i}) = O(s\sum^n_{i=1} \frac{1}{a_i})\),
平均情况下 \(T(n)=O(n\log s)\)
最坏情况下\(\forall i(1\leq i< n),a_i=1\),特别地,\(令a_n=10^5\),\(T(n)=O(ns)=O(n^2)\),理论上复杂度是不可以的,经过我的实际测试,对于这组数据:
100000 0
100000 1 1 1 1 ......(1e5-1 个 1)
可以把我如上思路完成的代码卡到60.8s才跑出来正确答案,所以我们需要特判一下\(a_i=1,k=0\)的情况。
代码如下
#include<bits/stdc++.h>
using namespace std;
const int N=100010;
typedef long long ll;
ll ans,n,K;
ll a[N],id[N*2],f[N],s; //s表示a[i]中最大的数
//lst[i]表示数i最后一次出现的下标,f[i]为左端点,i为右端点的子数组是以i为右端点的子数组中最长的
int main(){
cin>>n>>K;
for(int i=1; i<=n; i++) scanf("%lld",&a[i]),s=max(s,a[i]);
for(ll i=1; i<=n; i++){
ll t=f[i-1];
if(a[i]==1&&K==0) t=max(t,i-1);
else if(a[i]>K) for(int j=0; j+K<=s; j+=a[i]){
t=max(t,lst[j+K]);
}
ans+=(i-t);
f[i]=t;
lst[a[i]]=max(i,lst[a[i]]);
}
cout<<ans<<endl;
return 0;
}